4 Laws of Motion and Gravity
The cosmos is vast and searching for other life within it requires an understanding of how and why objects move. These questions are not new -- Aristotle and other Greek philosophers thought about them -- and it was through rigorous mathematical testing of observations against theory that allowed Isaac Newton to uncover gravity as the underlying force for the motion of the planets around the Sun. In this chapter, we examine the fundamental laws governing objects in motion and show examples of how to apply these laws to studying planets in other solar systems.
Learning Objectives
By the end of this chapter, you will be able to:
- Explain how Galileo disproved the idea that heavy objects fall faster than light ones.
- Understand how Newton’s Laws of Gravity explain Kepler’s Laws of Planetary Motion.
- Describe how free fall occurs for satellites in stable orbits about the Earth.
- Explain the difference between mass and weight and the concept of surface gravity.
Understanding Motion
Ancient Greece, from about 600 B.C. to 200 A.D, is notable in the history of science as a time when observations in nature began to be explained using rational thought and reasoning, rather than invoking supernatural explanations. As discussed in Appendix on the History of Astrobiology, the geocentric (meaning Earth is at the center) model of Ptolemy emerged as the accepted explanation of how the cosmos is organized and this model remained unchallenged until Copernicus proposed a heliocentric model in the early 1500s.
Contemplating different models of the cosmos necessitated thinking about why the bodies, celestial or otherwise, move (or don't move) in the way that they do. Physics, particularly kinematics and dynamics, was fundamental to this inquiry and the word physics itself is thought to come from the Greek word phusis, meaning nature. Aristotle posited that all objects on Earth seek their natural state of motion, which is to be at rest, unless some force is being applied to the object to keep it in motion. This idea has some aspects of the correct explanation of the motion of objects but misses the fact that an object in constant motion is also in its natural state. Aristotle also stated that heavier objects fall more quickly to the Earth than lighter objects. This is not correct but is easily tested. While Aristotle (or anyone else at this time) did not test this, Galileo conducted many physics experiments and did test this idea and ultimately falsified it.
Galileo also began to show that motions of objects in the heavens and objects on the ground were connected. Greek astronomy held that the motions in the celestial realm were different than the motions seen near the ground and, while the motion of planets and stars could be predicted very accurately, there was no unifying explanation for why things were moving they way they were seen to move. The general consensus was that things in the heaven moved "perfectly" in their own fashion based on ideal laws and patterns and many believed that the objects in the sky were made of substances that were fantastical, brilliant, and glorious unlike the dark, dirty, and "base" material found on Earth.
As for Aristotle's assertion that heavier objects fall faster to the Earth, Galileo found results that yielded a different rule. Galileo's motion experiments were consistent with all objects, regardless of their mass, falling at the same rate. Galileo found that this rate (known as an acceleration) is approximately a change in speed of 10 m/s for every second that an object is falling provided there is no resistance (such as friction) or extra force applied in the direction of falling. This constant acceleration of free fall would feature prominently in future developments of our understanding of gravity. It was used by Isaac Newton to show that mass is what causes gravity and was used by Albert Einstein to argue that gravity was indistinguishable from a reference frame that is under a similar sort of acceleration (this is his so-called equivalence principle).
The video clip below shows confirmation by Apollo 15 astronauts on the Moon that all objects fall at the same speed (the Moon is a great place to test this since there is no air) in the absence of air resistance.
In regards to the natural state of an object, Galileo showed that the motion of objects on Earth under the right conditions can continue to move forever without any forces being applied to them. This is the basis of inertia, which is the tendency of objects to keep doing what they are already doing. In other words, a stationary object stays put, and a moving object keeps moving unless some force intervenes. Objects speeding along at a constant velocity were physically indistinguishable from objects at rest and Galileo proved this by comparing the movement of objects falling to the ground, rolling down ramps, and flying through the air as projectiles. No matter what the situation, the motion of objects parallel to the ground was completely independent of the falling towards the Earth, and it seemed that the ideal scenario was one where such motion would continue forever unless or until something stopped it. Isaac Newton's first law of motion would further clarify this state of affairs by elegantly stating: in the absence of external forces, objects in motion stay in motion and objects at rest stay at rest.
To show that the motion of objects in the heavens obeyed these same rules was a bit harder to explain and some more further insight was needed to connect the two. Kepler's law of motion provided a mathematical framework for the motions of planets but Kepler didn't know that gravity was the unifying concept that would explain this motion. This was left to Newton who figured out that the same force that caused objects to fall to Earth could also explain all the celestial motions.
Kepler's Laws of Motion
Kepler inherited a very accurate catalog of planetary positions that Tycho Brahe meticulously collected over several decades. Through his analysis of the motions of the planets, Kepler empirically developed a series of principles, now known as Kepler’s three laws, which described the behavior of planets based on their paths through space. The first two laws of planetary motion were published in 1609 in The New Astronomy. Their discovery was a profound step in the development of modern science.
Kepler's First Law
Kepler's First Law states planets orbit the Sun in the shape of an ellipse, with the Sun at one focus. The discovery that planetary orbits are ellipses brought down the long-held belief, going back to Plato and Aristotle, that the orbits were perfect circles.
The path of an object through space is called its orbit. Kepler initially assumed that the orbits of planets were circles, but doing so did not allow him to find orbits that were consistent with Brahe’s observations. Working with the data for Mars, he eventually discovered that the orbit of that planet had the shape of a somewhat flattened circle, or ellipse. Next to the circle, the ellipse is the simplest kind of closed curve, belonging to a family of curves known as conic sections.
A circle is a special case of an ellipse. We can think of an ellipse in general as a flattened circle. The amount of flattening of an ellipse is called its eccentricity or e. The eccentricity of an ellipse varies from 0 to 1. A circle has an eccentricity of 0. Any ellipse also has two interior points called foci (singular: focus); these are labeled f1 and f2 in Figure 1 below. As the eccentricity of an ellipse increases, the foci get further away from the center. For a circle, there is only one focus and it is at the center. As we'll see, the eccentricity for the orbits of most of the planets in our solar system are very close to zero, with Mercury being the exception with an eccentricity of 0.21. If the eccentricity of a planet's orbit is close to zero, this means that it is very close to being circular motion but, importantly, the distance between the planet and the Sun is not constant.
In the mathematical description of an ellipse, the distance from the center of the ellipse to the widest part of the ellipse is the semi-major axis, a. This means the diameter of an ellipse is 2a. The semi-major axis of a planetary orbit is the average distance of the planet from the Sun. Note that the second focus of the ellipse is empty, meaning there is physically nothing there. We can define two important points on a planet's orbit: perihelion and aphelion. Perihelion is when a planet is closest to the Sun and aphelion is when the planet is at its furthest distance from the Sun.
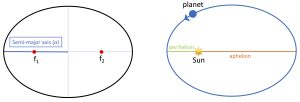
*You can explore the properties of an ellipse using the simulation at the end of the chapter below.*
Kepler's Second Law
Kepler’s second law deals with the speed with which each planet moves along its ellipse, also known as its orbital speed. Working with Brahe’s observations of Mars, Kepler discovered that the planet speeds up as it comes closer to the Sun and slows down as it pulls away from the Sun. Kepler's second law is called the law of equal areas and states that a planet will sweep out equal areas in an orbit in equal time intervals. Note that the planet does not sweep out equal angles in equal time intervals unless the orbit is a circle. In Figure 2 below, the triangular area B, defined by the Sun and points 1 and 2, has an area equal to the triangular area A, defined by the Sun and points 3 and 4.
Kepler's second law has important implications. Clearly the distance between points 3 and 4 is shorter than the distance between points 1 and 2 in Figure 2 below. Since the time interval is the same for these different distances, the planet is traveling at different velocities. A planet moves fastest when it is closest to the Sun (at perihelion) and slowest when it is furthest from the Sun (at aphelion).
Kepler's Third Law
About a decade after Kepler had formulated his first two rules for the motion of planets in the solar system, he published a third law based on his empirical data, which says that the square of the orbital period is proportional to the cube of the semi-major axis:
[latex]P^2 \propto a^3[/latex]
where ais the semi-major axis of the elliptical orbit and P is the orbital period and the [latex]\propto[/latex] symbol is read as "proportional to". When P is measured in years, and a is expressed in astronomical units (AU), the two sides of the formula are not only proportional but equal:
[latex]P^2 = a^3[/latex]
This means that a planet that is closer to the Sun has a shorter orbital period than a planet that orbits farther away. Mercury completes one orbit in 88 days, Venus orbits in 225 days, and the Earth takes 365 days to travel around the Sun. Kepler’s third law applies to all objects orbiting the Sun, including Earth, and provides a means for calculating their relative distances from the Sun from the time they take to orbit.
Worked Example: Using Kepler's Third Law
Example 1. Let's start by using Kepler's Third Law to find the orbital period of Jupiter. The semi-major axis of Jupiter's orbit around the Sun is 5.20 AU. Recall that the semi-major axis, a, is equivalent to the average distance of a planet from the Sun.
[latex]P^2 = a^3[/latex]
We can solve for P by taking the square root (which is the same as raising a number to the 1/2 power) of each side of the equation: [latex](P^2)^\frac{1}{2} = (a^3)^\frac{1}{2}[/latex]
[latex]P = a^\frac{3}{2}[/latex]
Putting in the value of a for Jupiter, and noting that if we have the semi-major axis in AU, then the orbital period will be in years:
[latex]P_{J} = a_{J}^\frac{3}{2}[/latex] = (5.20)3/2 = 11.9 years
Example 2. Now let's use Kepler's Third Law to find the average distance that Halley's Comet is from the Sun. It takes Halley's Comet 76 years to make one orbit around the Sun (and it last visited the solar neighborhood in 1986). The average distance of Haley's comet is found by solving Kepler's Third Law equation for a, this time by taking the cube root (or 1/3 power) of each side: [latex](a^3)^\frac{1}{3} = (P^2)^\frac{1}{3}[/latex]
[latex]a = P^{2/3}[/latex] = (76)2/3 = 17.9 AU
This means the average distance of Halley's comet from the Sun is 17.9 AU. In reality, Halley's Comet has a very elliptical orbit, with an eccentricity of e = 0.97. You can easily carry out one more step to find the minimum and maximum distance (in this case, the perihelion and aphelion distances) of the comet from the Sun:
dperihelion = a(1 - e) and daphelion = a(1 + e)
dperihelion = 17.9 AU (1 - 0.97) = 0.537 AU
daphelion = 17.9 AU (1 + 0.97) = 35.3 AU
Newton's Principia
Isaac Newton was born the same year that Galileo died: 1642. While he was a college student at Cambridge in the UK, the Bubonic plague swept through London. Newton worked from home during the quarantine (sound familiar?) and had an immensely productive time during his isolation in 1665-1666. Newton continued to work on his ideas in private, even inventing new mathematical tools, such as Calculus, to help him deal with the complexities involved. Eventually, his friend Edmund Halley prevailed on him to collect and publish the results of his remarkable investigations on motion and gravity. The result was a volume that set out the underlying system of the physical world, Philosophiae Naturalis Principia Mathematica. The Principia, as the book is generally known, was published at Halley’s expense in 1687.
Newton's Laws of Motion are:
- Newton's First Law (Law of inertia): Every object will continue to be in a state of rest or move at a constant speed in a straight line unless it is compelled to change by an outside force.
- Newton's Second Law: The change of motion of a body is proportional to and in the direction of the force acting on it. This is often stated as the equation F = ma, or force equals mass times acceleration.
- Newton's Third Law: For every action, there is an equal and opposite reaction.
Here are some examples of each of Newton's laws of motion to help further elucidate their meaning in the context of astrobiology. Newton's first law means that an object that is coasting in space, far from the forces from any other objects, will continue coasting at the same speed. This is seen for the Voyager spacecraft. Voyager 1 and 2 were launched in 1977 and have travelled out past the edge of the Kuiper Belt. Unless their orbits take them close to another object, the spacecraft will both continue coasting at a constant speed (Voyager 1 is moving at about 38,000 miles per hour and Voyager 2 at 34,400 miles per hour).
In the Space Flight chapter, we discuss sending a light sail out to visit the nearby (4 light years away) exoplanet Proxima b. After a force is initially applied to speed up the light sail, it will coast at a constant speed of about 100 million miles per hour (45,000 km/s) until it reaches the Proxima star system.
Newton's second law tells us how to speed up (or slow down or change the direction of motion of) an object: by applying a force. The rate of change in an object’s velocity is called acceleration. Newton showed that the acceleration of a body was proportional to the force being applied to it. A larger force will lead to a larger acceleration, meaning a greater change in motion. For example, the larger the force applied to a light sail sent to another star, the faster the sail will be able to travel.
Newton's third law means that if you push on something, it pushes back. You pushing on something is the action, and the something pushing back with the exact same force is the reaction. An example of action-reaction forces is familiar to all who have batted a baseball (or shot a rifle). The recoil you feel as you swing your bat shows that the ball exerts a force on it during the impact, just as the bat does on the ball. A more pertinent example for astrobiology is rocket motion. The force that discharges the exhaust gases from the rear of the rocket is accompanied by the force that pushes the rocket forward; the exhaust gas pushed through the back is the action and the rocket moving forward is the reaction. The exhaust gases need not push against air or Earth; a rocket actually operates best in a vacuum.
Newton's Universal Law of Gravitation
Kepler used Tycho's measurements of the planet positions over time to empirically derive the mathematical relationship captured in Kepler's third law. However, Kepler did not have a physical explanation for why the planets orbited the Sun. This is a good example of how science works. We make observations, try to fit the observations with a mathematical model, and then look for an elegant generalization that is both descriptive and predictive. If the mathematical generalization holds up under intense scrutiny, it is elevated to have the status of a theory.
About sixty years after Kepler published his third law for how the motion of planets in our solar system behaved, Isaac Newton helped us to understand the "why." Newton developed a mathematical description of gravity as a force between two objects that is proportional to the product of the object masses (M1 and M2) and inversely proportional to the square of the distance, d, between them measured from center to center; G is Newton's Universal Gravitational Constant which sets the strength of gravity throughout the universe and is equal to :
[latex]F_{grav} = G \frac{M_{1} M_{2}}{d^2}[/latex]
This is Newton's Universal Law of Gravitation and it tells us that the the closer together the objects are (that is, the smaller the value of d), the stronger the force between the two will be. It also tells us that the more mass an object has, the stronger the pull of its gravitational force.
We make an important note here that Newtonian Gravity, as we are discussing it here, is not the full story. Albert Einstein showed that mass itself creates gravity by warping the spacetime around it.
Revisiting Kepler's Third Law
Newton's law of gravitation shows that mass and gravity are directly related to each other. When Newton reanalyzed Kepler's Third Law through the lens of gravity, he found that the mass of the star and the planet also appear in the relationship as:
[latex](M_{1}+M_{2})P^2 = a^3[/latex]
Here, M1 and M2 are the masses of the two objects that are in orbit, for example a planet orbiting the Sun or a moon orbiting a planet. Technically, both objects are orbiting what is know as the center-of-mass between them, but we will visit this concept in more detail when discussing methods for detecting exoplanets.
The mass of a star is vastly greater than the mass of a planet (or even more so for a comet) so we can ignore the mass of the smaller object and use only the mass of the star. This same logic applies if a moon is orbiting a planet and the planet's mass is much greater than the moon's mass, which is the case for Earth. We can thus eliminate the mass of the much lighter object and write the relationship as:
[latex]M P^2 = a^3[/latex]
where M is the mass of the much heavier object. To use Newton's version of Kepler's Third Law as shown above, the semi-major axis a needs to be in AU, the orbital period P in years, and the mass must be reported in solar masses (where the Sun has a value of 1 and a star twice as massive as the Sun has the value 2). We will look at some examples in the box below to show how fundamental Newton's version of Kepler's Third Law is for understanding other solar systems.
Worked Example: Using Newton's Version of Kepler's Third Law
Example 1. Consider a planet orbiting a star that is one-half the mass of the Sun (Mstar = 0.5 MSun). The planet takes 730.5 days to make one orbit around the star. What is the semi-major axis of the planet's orbit?
First, we need to convert the units for the orbital period into years:
(730.5 days) × (1 year/365.25 days) = 2 years
Now, we can use this value, along with the mass of the star, to find a; first, we solve for a by taking the cube root of both sides:
[latex](a^3)^\frac{1}{3} = (M P^2)^\frac{1}{3}[/latex]
[latex]a = (M \times P^2)^\frac{1}{3} = (0.5 \times 2^2)^\frac{1}{3} = (0.5 \times 4)^\frac{1}{3} = 2^\frac{1}{3} = 1.26[/latex] AU
Example 2. Now let's turn the problem around and find the orbital period for a planet if we are given the semi-major axis of the planet's orbit and the mass of the star. If the planet is orbiting with a semi-major axis a of 4.0 AU around a star that is three-times more massive than the Sun, how long does it take this planet to make one orbit around the star?
This time, let's solve Newton's version of Kepler's Third Law for P:
[latex](P^2)^\frac{1}{2} = (a^3/M)^\frac{1}{2}[/latex]
[latex]P = (a^3/M)^\frac{1}{2} = (4^3/3)^\frac{1}{2} = (64/3)^\frac{1}{2} = 4.62[/latex] years
Learn More About: Orbital and Escape Speed
Newton's Law of gravity can be combined with his laws of motion to derive the speed of a planet as it orbits a star or, more generally, the speed of any object revolving around another object.
For an object in a circular orbit, the orbital speed is given by:
[latex]v_{orbit} = \sqrt{\frac{GM}{R}}[/latex]
where M is the mass of the body about which the object orbits, R is the radius of the orbit (how far away it is from the center) and G is the universal gravitation constant. This is the speed needed to launch an object such as a satellite into orbit around the Earth (vc in Figure 3a) or the average speed of a planet orbiting a star.
What if we want the object to leave (escape) Earth's orbit? The equation for the escape speed is very similar, but now the speed is higher by a factor of [latex]\sqrt{2}[/latex]:
[latex]v_{escape} = \sqrt{\frac{2GM}{R}}[/latex]
It makes sense that a higher speed, meaning more force, is needed to get an object out of orbit. What about speeds that are in between those for a circular orbit and the escape speed? These will result in bound elliptical orbits for the object; at the escape speed, the object becomes unbound from the Earth's gravity.
The equation above for the orbital speed of an object is specifically for a circular orbit. Planetary orbits around the Sun are not circular but are elliptical, so we must keep in mind that the actual speed of the planet varies as it revolves around the Sun. For a nearly circular orbit like the Earth, with an eccentricity e of 0.017, the deviation from the circular orbit is only a few km/s, but you can imagine that this breaks down for a highly eccentric object like that for Halley's comet. An exact speed can be found for elliptical orbits by taking the eccentricity into account.
One final note is that any satellite orbiting another object -- be it a weather satellite orbiting the Earth, a moon orbiting a planet, or a planet orbiting a star -- obey these laws. Kepler's and Newton's laws are universal.
Free Fall, Weight and Surface Gravity
Free Fall and Weightlessness
An object that only has the force of gravity acting upon it is in free fall. This can be a confusing concept, as it certainly looks like the astronauts on the International Space Station (ISS) are in an environment with no gravity, as they are floating around - but there is in fact gravity at the height that the ISS orbits. What is happening? The astronauts are experiencing the sensation of weightlessness; you may have felt this sensation if you have been on a ride at an amusement park that lifts you up out of your seat momentarily. But the astronauts still have weight, just as you still do on a roller coaster ride. With the astronauts on the ISS, they are in free fall around the Earth, not to Earth. As the ISS is pulled to the Earth's surface due to gravity, the motion (speed) of the ISS is fast enough to prevent it from actually falling to the Earth...and it stays in orbit. This is shown in Figure 3(a) above.
Mass, Weight and Surface Gravity
You may have heard that you weigh less on the Moon than you do on Earth. This is true! How can that be? The key here is that mass and weight are not the same. Your mass (measured in kilograms, usually) is the same no matter where you are; your weight depends on the surface gravity of where the scale you are standing on is located. And the Moon has a lower surface gravity than the Earth.
Using Newton's laws of motion and gravity, we can show that the surface gravity g on a world is:
[latex]g = \frac{GM}{R^2}[/latex]
where M is the mass of the world and R is its radius. We can look up the mass and radius of the Earth (MEarth = 5.97×1024 kg; REarth = 6.38×106 m) and the value of the constant G (6.67×10-11 m3 kg-1 s-2) and find that:
gEarth = 9.8 m/s2
Note that the units for the radius and mass need to be consistent with those for the constant G for the equation to give the correct result.
We are interested in knowing the surface gravity of planets orbiting other stars to assess the habitability of the planet. We can find this quickly if we know the mass and radius relative to Earth, as shown in the example below.
Worked Example: Surface Gravity of an Exoplanet
The exoplanet Proxima b is of interest to astrobiologists as it is orbits in the "habitable zone" around its star. Proxima b has a mass that is 1.07 times that of the Earth (MProx = 1.07 MEarth) and a radius that is 1.03 times the radius of the Earth (RProx = 1.03 REarth). Note that this means that Proxima is almost the same size as the Earth but has a slightly larger mass (7% larger than the Earth's mass) and radius (3% greater than the Earth's radius). If we take the ratio of the surface gravity of the Earth to that of Proxima b, the gravitational constant G cancels out and we are left with the following ratio:
[latex]\frac{g_{P}}{g_{E}} = \frac{GM_{P}/R_{P}^2}{GM_{E}/R_{E}^2} = \frac{M_{P}}{M_{E}} \sqrt{\frac{R_{P}}{R_{E}}}[/latex]
[latex]g_{P} = \frac{1.07 M_{E}}{M_{E}} \sqrt{\frac{1.03 R_{E}}{R_{E}}} g_{E} = 1.07 \sqrt{1.03} g_{E} = 1.08 g_{E}[/latex]
The surface gravity on Proxima b is very close to that on the Earth's surface and is 8% higher. In other words: gP = (1.08) gEarth = 1.08 (9.8 m/s2) = 10.6 m/s2
Data source: https://exoplanets.nasa.gov/eyes-on-exoplanets/#/planet/Proxima_Cen_b/
Once you know the surface gravity of a world, you can easily calculate how much you would weigh if you were standing on a scale on its surface. From Newton's second law, we know that force is equal to mass times acceleration. Standing on the surface, your acceleration is that due to gravity:
Weight = (mass)×(surface gravity) = mg
Worked Example: Weight
The surface gravity on the Moon is 1.62 m/s2, which is about one-sixth the value on Earth's surface. How much would you weigh if you stepped on a scale on the Moon?
We can use the relationship between weight, mass and surface gravity to solve this. Let's assume a weight of 100 kg. We can quickly show the weight on Earth's surface for a person with this mass:
WEarth = mgEarth= (100 kg)×(9.8 m/s2) = 980 newtons = 980 N
Notice that the units of weight are in newtons. This is a unit of force, named in honor of Sir Isaac Newton, that is abbreviated as N. In the U.S., many scales show weight in pounds, and 1 pound is equal to 4.45 N. Therefore,
(980 N)×(1 pound/4.45N) = 220 pounds = 220 lbs
Now, let's do this calculation for the Moon:
WMoon = mgMoon= (100 kg)×(1.62 m/s2) = 162 N
(162 N)×(1 pound/4.45N) = 36.4 pounds = 36.4 lbs
Another way to solve tis problem is to take the ratio of your weight on the Moon to your weight on Earth; doing this leaves the simple formula:
WMoon = (gMoon/gEarth)×WEarth
WMoon = (1.62 m/s2/9.8 m/s2)×220 lbs
WMoon = 0.1653×220 lbs = 36.4 lbs
This way of solving the problem avoids the need to convert the units for the weight.
Calculate the weight for this same person (with a mass of 100 kg) on the surface of Proxima b.
Show Answer
We found in the previous example that the surface gravity on Proxima b is 10.6 m/s2. Using this value:
WProxb = mgProxb= (100 kg)×(10.6 m/s2) = 1060 N
(1060 N)×(1 pound/4.45N) = 238 pounds = 238 lbs
General Relativity
In 1915, Einstein published his General Theory of Relativity, treating gravity as a warping of the space-time continuum and an attribute of mass rather than a fundamental force. Einstein's description of gravity employs mathematically sophisticated metric tensors, while Newtonian gravity uses more commonly accessible algebra or calculus. On the scales that humans are accustomed to working with (and certainly for the physics included in this course), general relativity converges to the Newtonian description, so we are justified in defaulting to the Newtonian description of gravity.
Key Concepts and Summary
Galileo demonstrated that heavier, more massive objects fall at the same rate as light objects. This can seem counter-intuitive because light objects often experience more wind resistance than heavier ones, but was beautifully demonstrated by astronauts on the airless moon. Kepler used data from his mentor, Tycho Brahe, to demonstrate three laws of planetary motion: planetary orbits are ellipses (not circles), the speed of planets was fastest during the closest approach to the Sun, the orbital distance (a) and orbital period (P) are mathematically related by [latex]P^2 = a^3[/latex]. Isaac Newton developed the branch of mathematics known as calculus to describe gravitational forces and showed that this matched Kepler's Third Law. Although gravity is now understood to be a property of mass that is more completely described by Einstein's General Theory of Relativity, Kepler's Law and Newton's Law of Gravity are accurate descriptions for most observations of orbital motion.
Review Questions
Summary Questions
- How did Galileo show that objects all fall at the same rate, regardless of their mass?
- Summarize Newton’s Laws of Motion and give a simple example that illustrates each law.
- Explain each of Kepler’s Laws of Planetary Motion.
- What does Kepler's Second Law say about the speed of a planet as it orbits the Sun?
- Explain in words Kepler's Third Law. Give an example of a problem we can solve using Kepler's Third Law. Now solve the problem!
- Explain Newtonian gravity and how gravity depends on mass.
- What does it mean to say an object is "in free fall"?
- What is the difference between mass and weight? Do your mass and weight change on the Moon? Explain why or why not.
- Explain what the surface gravity of a world means. Give an example of two planets or Moon's with different surface gravities and explain how they differ.
- Briefly explain why we do not need to use Einstein's laws of relativity to study the orbits of planets.
Exercises
- Planetary Orbit Simulator. Open the simulator here.
- The default is set to the planet Mercury. Click on "show center". How close is the Sun to the center? Now switch to planet Earth. How close is the Sun to the center? Note the difference in eccentricities for Mercury and Earth.
- Click on the "Kepler's Second Law" tab.
- Gravity and Orbits. Open the Gravity and Orbits simulation here.
- To start, select the To Scale option in the simulation as we would like to have an experiment that is as close as possible to the way things are in reality. This option adjusts the physical sizes of objects so that they take up the correct amount of space relative to their orbital motions. Because the scale of orbits is so much larger than the physical size of the stars, planets, moons, and satellites, in the To Scale option, you won't be able to see many of the objects beyond tiny points.
- Enable the "Mass", "Path", and "Grid" options. You will notice that the system we are simulating is the Earth-Sun system. Note the position of the Earth at the start of the simulation. It is at the intersection of a particular set of grid points.
- Now start to run the simulation. You will see the planet (Earth) begin to orbit the star (the Sun). Try to time it so that you can determine the amount of time it takes for the planet to complete one revolution around the Sun. You should note that it takes about 365 days for the planet to return to that initial grid point. This means the simulation is working since that is indeed the amount of time it should take a planet that is the distance from the Sun of one astronomical unit (AU) to make a complete orbit!
- If the Earth suddenly gained mass, what do you think would happen to the length of a year? Run the simulation for a more massive Earth to see if your intuition was correct.
- What if the Earth suddenly lost mass?
- If the Sun suddenly gained mass, what do you think would happen to the length of a year?
