2 Energy and Light
Life needs a source of energy to thrive. This energy can come in different forms, from sunlight to energy released when chemicals react. Light is a type of pure energy, and coded into the light and other kinds of radiation that reach us from objects in the universe is a wide range of information about what those objects are like and how they work. If we can decipher this code and read the messages it contains, we can learn an enormous amount about the cosmos without ever having to leave Earth or its immediate environment.
Learning Objectives
By the end of this chapter, you will be able to:
- Understand that there are different types of energy and that energy is conserved
- Explain the wavelength, frequency and energy of a wave or particle of light
- Discuss the different parts of the electromagnetic spectrum
- Explain how and why the light emitted by an object depends on its temperature
- Explain the difference between the luminosity and brightness of an object
- Explain how the total energy emitted differs for hot and cold objects
Energy
Different types of energy are all around us — the electrical energy that powers our technology, the chemical energy that is stored in the food we eat, and the heat energy we feel when when walking in sunlight. These different types of energy can be changed, or converted, from one type to another. For example, the chemical energy in food is converted to energy that allows us to think and move around. We will see other examples of energy transformations in astrobiology, such as the gravitational energy that is converted into heat when a giant cloud of gas and dust collapses and eventually forms stars.
The amount of the energy in the universe is always the same and it is continuously being changed from one form into another. This is the essence of the law of conservation of energy. Other quantities in nature, such as mass and momentum, are also conserved.
Though energy cannot be created or destroyed, it can be transformed into different forms. The two main forms of energy are kinetic energy and potential energy. Kinetic energy is the energy of motion. When an object is moving more quickly, it has more energy. A fast-moving car has more energy than a slow moving car. Thermal energy is actually a form of kinetic energy since higher temperature is really a measure of the average speed of atoms and molecules — the higher the temperature, the greater the kinetic energy of the atoms and molecules.
Potential energy is the energy that is associated with different positions in space. When you throw a ball high into the air, it has more gravitational potential energy than when it is held in your hand. When an object moves from an area of high potential energy to low potential energy, that energy will be transformed into another form. For example, when an apple falls to the Earth, it will speed up gaining kinetic energy. But potential energy does not need to be related just to gravity. For example, the energy stored in chemicals is in the form of chemical potential energy which can be determined based on the position of different atoms bonded to each other by electric forces of attraction.
A more recently discovered form of energy is the energy associated with mass itself. Einstein’s famous equation [latex]E=mc^2[/latex] tells us, that mass-energy equivalence is a fundamental feature of the universe. Any object that has mass therefore also contains energy — this type of energy is called rest-mass energy. Inside the core of stars, nuclear fusion converts some of the rest-mass of two protons into energy. This process occurs an astounding 1038 times every second and is the source of the energy from the Sun that we receive on Earth.
Light
A great deal of the energy that life on Earth uses comes in one way or another from the Sun’s light, although geothermal energy from inside the Earth can also be harnessed. Light from the Sun, or any star, is an example of electromagnetic radiation. Here, the words light and radiation are synonymous, and both are a form of energy. Radiation can sometimes be thought of as dangerous and some types are (for example, gamma rays and X rays), but radiation is a neutral term and is synonymous with energy.
One of the more bizarre aspects of light is the way that it acts, specifically the fact that it can behave like a wave and a particle. In the 17th century, the nature of light was debated and both Isaac Newton and Christiaan Huygens tried to explain it. Newton experimented with lenses and prisms and believed that light was a stream of particles, which he called corpuscles. Huygens, on the other hand, believed that light was a wave that traveled outward in all directions from a source, much like the ripples on a pond that expand outward through the water after a stone is dropped into it. Building upon pioneering work by James Clerk Maxwell and Max Planck, Albert Einstein proposed in 1905 that light can indeed behave both ways, thus solidifying the concept of wave-particle duality, one of the tenets of quantum mechanics. The wave and particle nature of light has now been experimentally verified countless times.
Light as a Wave
Light carries energy and information from one place to another, and this energy is carried in the form of electromagnetic (EM) waves. Other familiar types of waves in nature include sound waves and water waves. All three of these types of waves have some differences and some similarities.
Water and sound waves are mechanical waves and require a medium to travel in. For sound waves, the medium is air and the medium is water for water waves. If you screamed on the surface of the Moon, which has no atmosphere, nobody would hear you as the sound waves have no medium to travel through. (The director Stanley Kubrick got it right in the film 2001: A Space Odyssey.) EM waves do not require water or air or any medium to travel though – they can travel through empty space. This was such a disturbing idea to nineteenth-century scientists that they actually made up a substance to fill all of space—one for which there was no evidence—just so light waves could have something to travel through: they called it the aether. Today, we know that there is no aether and that EM waves have no trouble at all moving through empty space (as all the starlight visible on a clear night must surely be doing).
The speed of a sound wave depends on the medium through which it is traveling. A sound wave moves faster through water than it does through air, for example. However, all electromagnetic waves move at the same speed in empty space (the speed of light—approximately 300,000 kilometers per second, or 300,000,000 meters per second, which can also be written as 3×108 m/s), which turns out to be the fastest possible speed in the universe.
Now for some similarities. All waves are a kind of repeating phenomenon. Whether it is the up-and-down motion of a water wave or the changing electric and magnetic fields in a wave of light, the pattern of disturbance repeats in a cyclical way. Thus, any wave motion can be characterized by a series of crests and troughs. Moving from one crest through a trough to the next crest completes one cycle. The horizontal length covered by one cycle is called the wavelength (λ). Ocean waves provide an analogy: the wavelength is the distance that separates successive wave crests. An example of water waves created when a frog leaps into a pond is shown in Figure 1.
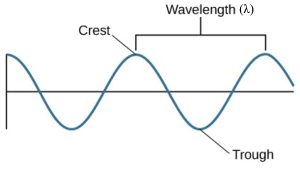
We can also characterize different waves by their frequency, which is the number of wave cycles that pass by per second. If you count 10 crests moving by each second, for example, then the frequency is 10 cycles per second (cps). In honor of Heinrich Hertz, the late nineteenth physicist who, inspired by physicist James Clerk Maxwell’s work, discovered radio waves, a cps is also called a hertz (Hz). Take a look at your radio, for example, and you will see the channel assigned to each radio station is characterized by its frequency, usually in units of kHz (kilohertz, or thousands of hertz) or MHz (megahertz, or millions of hertz).
Concept Check: Wavelength and Frequency
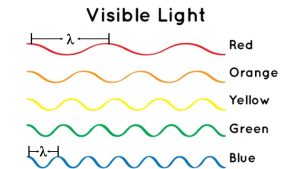
Figure 3 is a schematic showing the wavelengths and frequencies for different colors of light. Red light is at the top and its wavelength (λ) is shown as the distance between two peaks, where the peaks are marked by the vertical black lines. Blue light is on the bottom; notice that it has a shorter wavelength than red light (the length between the two peaks is noticeably shorter).
The frequency of a wave is a measure of how many waves pass by in one second. Let’s imagine that the amount of time that elapsed for each of the waves in Figure 3 is 1 second. Looking at red light, two full waves can pass by in this 1 second period, so we say the frequency is 2 cycles per second, or 2 Hz. (Actually, a bit more than two red light wave cycles can pass by, about 2.5, but we will say 2 full waves to keep this example simple.)
- Which color of light has the highest frequency? How about the lowest frequency?
- Which color of light has the shortest wavelength?
Show Answer
- Looking at Figure 3, the most crests pass by in one second for blue light (6 Hz) while the fewest pass by for red light. Thus, blue light has the highest frequency and red light has the lowest.
- Since blue light has the highest frequency, it also has the shortest wavelength. It is easy to see in Figure 3 that λ is shortest for blue light.
Wavelength (λ) and frequency (f) are related because all electromagnetic waves travel at the same speed. The formula for this relationship can be expressed as follows: for any wave motion, the speed at which a wave moves equals the frequency times the wavelength. Waves with longer wavelengths have lower frequencies. Mathematically, we can express this as
[latex]$$c = \lambda f $$[/latex]
where the Greek letter for “l”—lambda, λ—is used to denote wavelength and c is the scientific symbol for the speed of light.
The electromagnetic wave model of light (as formulated by James Clerk Maxwell) was one of the great triumphs of nineteenth-century science. In 1887, when Heinrich Hertz actually made invisible electromagnetic waves (what today are called radio waves) on one side of a room and detected them on the other side, it ushered in a new era that led to the modern age of telecommunications. His experiment ultimately led to the technologies of television, cell phones, and today’s wireless networks around the globe.
Light as a Photon
By the beginning of the twentieth century, physicists had to reluctantly accept that sometimes light behaves more like a “particle”—or at least a self-contained packet of energy—than a wave. We call such a packet of electromagnetic energy a photon.
A photon carries a specific amount of energy. How much energy a photon has depends on its frequency. We can use the idea of energy to connect the photon and wave models. How much energy a photon has depends on its frequency. A low-energy radio wave has a low frequency, while a high-energy X-ray at your dentist’s office is a high-frequency wave. Among the colors of visible light, violet-light photons have the highest energy and red-light photons have the lowest.
Test whether the connection between photons and waves is clear to you. In the above example, which photon would have the longer wavelength as a wave: the radio wave or the X-ray? If you answered the radio wave, you are correct. Radio waves have a lower frequency, so the wave cycles are longer
The Electromagnetic Spectrum
Objects in the universe send out an enormous range of radiation, or light. Scientists call this range the electromagnetic (EM) spectrum, which are divided into a number of regions. The spectrum is shown in Figure 4, with some information about the waves in each part or band.

Looking at the EM spectrum in Figure 4, we see that:
- Gamma rays have the highest energy and radio waves have the lowest energy
- Radio waves have the longest wavelength and gamma rays have the shortest wavelength
- Radio waves have the highest frequency and gamma rays have the lowest frequency
These properties of light are summarized by the beautifully simple equation that relates the energy of a photon to its frequency (or wavelength), where h is Planck’s constant:
[latex]E=hf[/latex]
This relationship shows the wave-particle duality of light, as the energy of photon (a particle of light) is directly related to its frequency (a wave property). Since h has a constant value, you can immediately get the energy of a particular color of light simply by knowing its frequency (or wavelength, which can be expressed as [latex]\lambda = c / f[/latex]).
Another property of light that has already been mentioned but is worth re-emphasizing is that all types of light travel at the speed of light. Since the speed of light is constant, all light travels at the same speed.
Worked Example: Frequency and Wavelength
Red light has a wavelength of about 650 nm and blue light has a wavelength of about 450 nm. Recall that nm is the abbreviation for nanometers.
What is the frequency of red light?
The frequency of any type of light is related to its wavelength as [latex]f = c / \lambda[/latex], where c is the speed of light.
To use this equation, we must be sure that the units are all consistent. If we use 3×108 m/s for the speed of light, then the wavelength must be in units of meters and the frequency will be in units of Hz (where 1 Hz = 1 cycle per second). So, we must first convert the wavelength from nanometers into meters. One nanometer is one-billionth of a meter: 1 nm = 10-9 m so it follows that 650 nm = 650×10-9 m. Expressed in scientific notation, the wavelength of red light is 6.50×10-7 m.
[latex]f = c / \lambda[/latex] = (3×108 m/s) ⁄ (6.50×10-7 m) = 461,538,461,538,461 Hz
That’s a huge number of cycles in one second! Expressing this in scientific notation, f = 4.62×1014 Hz.
The wavelength of visible light (like red and blue) is often reported in THz, where T is the prefix one trillion, or 1012.
Extra 1: Show that the frequency can also be expressed as 462 THz.
Show Answer
The frequency 4.62×1014 Hz can also be written as 4.62×102×1012 Hz
4.62×102 = 462 and 1012 Hz = 1 THZ, so f = 462 THz
Extra 2: Show that the frequency of blue light (with a wavelength of 450 nm) is 666 THz.
Show Answer
[latex]f = c / \lambda[/latex] = (3×108 m/s) ⁄ (4.50×10-7 m) = 6.66×1014 Hz = 666 THz
Types of Electromagnetic Radiation
Throughout our study of astrobiology, we will encounter all types of light. When we collect light using a camera or sensor on the Earth’s surface, that light must first travel through the Earth’s atmosphere before it reaches the ground. Depending on the type of light, some of it may be partially or completely absorbed by molecules in different parts of the Earth’s atmosphere. This means that some types of telescopes need to be above the Earth’s atmosphere in order to detect any light. Also, we will see that this absorbed light will show up as a kind of set of Earth’s chemical fingerprints in any observations that contain the Earth’s atmosphere; this is the basic idea behind biosignatures for life, and we will probe it more deeply in the SETI chapters.
The way that light is absorbed in Earth’s atmosphere for each part of the EM spectrum is shown in Figure 5.
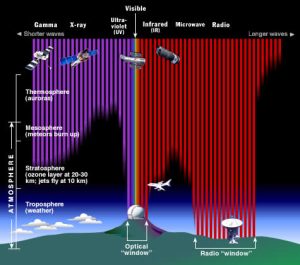
We highlight a few properties of each type of light that are of relevance to astrobiology, as well as what types of telescopes are used to study the universe in each type of light.
Radio Waves
Radio waves have the longest wavelengths of any type of radiation — they can range from a few millimeters all they way up to hundreds of kilometers (for reference, Switzerland is about 300 km across). Radio waves have very low energies and are all around us in our everyday lives. On Earth, cell phones, radio and TV transmissions, satellites and radar all emit radio waves and these pass right through our bodies. Radio waves are also produced in nature by a number of astrophysical objects, including stars and pulsars. The most abundant element in the cosmos — hydrogen — also naturally emits radio waves at a very specific wavelength of 21 cm (which corresponds to a frequency of 1420 MHz). As we will see later in the chapter on SETI, astronomers search for signals from advanced extraterrestrial civilizations that are close to the 21 cm radiation that hydrogen produces.

Most radio waves reach the ground, as seen by the “radio window” in Figure 5. The lowest frequency radio waves do not make it to the Earth’s surface and this region of the EM spectrum remains unexplored. Because radio waves are long, in general the telescopes (in the case of radio astronomy, these are called dishes or antennae) need to be very large. Some of the first radio observations made to look for signs of intelligent life were carried out by Frank Drake in 1960 using the 85-foot Green Bank Telescope. There is another way to work around the large size needed for dishes through a technique called interferometry. Using this technique, a number of small radio dishes can be made to work in concert and achieve the same precision as a larger dish. The Hat Creek Radio Observatory in northern California, for example, has 28 dishes that are each 6 meters and can all point to the same target on the sky and collectively function as a 40 m dish.
Microwaves
Microwaves are also low energy radiation and have sizes that range from about 1 mm up to 300 mm. The most familiar source of microwaves on Earth is probably microwave ovens. Microwaves are used extensively by satellites to monitor weather on the Earth (Doppler radar maps use microwaves) and for remote sensing of the Earth’s surface. The ancient radiation left over from the Big Bang also happens to fall into the microwave part of the EM spectrum. This Cosmic Microwave Background (CMB) radiation was discovered serendipitously in 1965 and has a wavelength of 1.9 mm. The CMB is literally everywhere on the sky and will appear as “background noise” in any observations that include this wavelength.
As seen in Figure 5, some microwave radiation makes it to the ground (the telescope used to detect the CMB in 1965 was on the ground in New Jersey, USA) but some parts are also absorbed by the Earth’s atmosphere. The COBE, WMAP, and Planck missions all studied the CMB in more detail and were space-based missions.
Infrared
Infrared light is given off by anything with a temperature. This discovery was made in 1800 by the astronomer William Herschel. Herschel studied the rainbow created when white light was sent through a prism and he found that the invisible region beyond the red edge of the rainbow was hotter than the temperature of the rainbow! Herschel called this type of radiation “calorific rays”, or heat rays, and today we refer to these heat rays as infrared (IR) light. Our eyes are only sensitive to visible light (some animals, such as vampire bats and goldfish, can see into the infrared), although we can still “see” this type of light by using an IR camera or night vision goggles. These types of sensors pick up differences in infrared intensity. Since most IR light gets absorbed by the Earth’s atmosphere, many IR telescopes are in space.

IR light is of great importance in astronomy because it can penetrate, or travel through, dust that is opaque to visible light. This idea is best shown with a comparison of the same picture taken in visible light and infrared light. Figure 7 shows pictures of the Carina Nebula taken by the Hubble Space Telescope (HST) in visible light (left) and infrared light (right). You can see an enormous amount of stars and other objects in the infrared that are not seen in the visible, as infrared light travels right through the dust while visible light is absorbed by the dust.
The James Webb Space Telescope (JWST), which launched in 2021 and has a mirror 2.7 times larger than the HST (meaning it can collect over 7 times as much light), detects IR light. IR light covers the range of about 1-1000 micrometers, where micrometers are abbreviated as μm and are often referred to as microns; for reference, E. Coli bacteria are 2 microns and a human hair is 100 microns. JWST can sense wavelengths in the range of 0.6-28 microns. One of the main goals of JWST is to study planetary systems and the origin of life. One way JWST is doing this is by studying the atmospheres of exoplanets to see if any molecules needed for life, as we know it, are present. This will be discussed in more detail in the chapters on exoplanets.
Visible Light
Human eyes evolved to detect wavelengths spanning the visible part of the EM spectrum, which covers 400 nm to 750 nm. Stars emit visible light and life on Earth would not exist without the light from the Sun. Microscopes and optical telescopes both take visible light and focus it into an image — the study of visible light is essential to astrobiology. For example, detailed pictures of the surface of Mars that show evidence for past liquid water are taken with visible cameras like Mastcam-Z on the Perseverance rover.
Visible light is not absorbed by the Earth’s atmosphere but it does get distorted as it passes through, thus causing images to become blurry. Stars as viewed from the Earth’s surface appear to twinkle for this reason. However, optical (visible) telescopes on the Earth’s surface can use techniques such as adaptive optics to correct for the atmospheric distortion of visible light. The Hubble Space Telescope does not need to worry about this when it collects visible light.
Some searches for intelligent extraterrestrial life in the universe are carried out using optical telescopes; these searches typically scan the sky and look for anomalous pulses, perhaps from lasers being used by a distant civilization.
Ultraviolet
Ultraviolet (UV) light has a shorter wavelength than visible light and ranges from about 10-400 nm. Stars hotter than the Sun emit primarily UV light but the Sun emits some UV light, too. This is probably most apparent when you are outside on a sunny day and forgot to bring some sunblock — your skin will absorb some of the UV (specifically, UVA) light. The fact that stars emit UV radiation is important for many aspects of life, in addition to protecting your skin. UV light can actually break the bonds between the hydrogen and oxygen atoms in a water molecule in a process called photolysis and this can create ozone in the atmosphere, which in turn protects life from dangerous radiation that can damage cells.
UV light is emitted from a range of astrophysical sources, including sites of star formation and planetary aurorae. As seen in Figure 5, nearly all UV radiation is absorbed by the Earth’s atmosphere so UV telescopes are almost always in space, although some telescopes on high mountain tops, like the Keck telescopes atop Mauna Kea in Hawaii, have UV instruments. NASA’s SWIFT satellite is actively studying the universe in UV light, and the Hubble Space Telescope has been probing a wide range of UV sources since 1990.
X Rays
X rays are a high energy type of radiation, with short wavelengths of just 0.01-10 nm, and they can be absorbed by tissue and bones in our bodies. They can destroy DNA so great care is taken when X ray machines are used to take medical images. Fortunately for life, X rays are absorbed by the Earth’s atmosphere so they are not a concern on Earth’s surface (but are a great concern for astronauts traveling above the Earth’s atmosphere).
X rays are generated by high energy astrophysical phenomena such as supernova as well as the Sun’s corona. During a total solar eclipse, the very hot gas in the Sun’s corona can be seen. The composition of soil on Mars is studied using X ray instruments on Martian rovers, such as Spirit and Opportunity and the active Perseverance mission.
Gamma Rays
Gamma rays are the most energetic type of radiation in the cosmos and have wavelengths on the order of the size of the nucleus inside an atom. On Earth, gamma rays are produced naturally by lightning and radioactivity. Gamma rays are also created when two neutron stars merge, in addition to the gravitational waves that these events create. Gamma rays produced in neutron star mergers produce many of the heavy elements on the periodic table, such as gold and platinum.
Gamma rays do not make it to the Earth’s surface so gamma ray observatories need to be in space. The Fermi Space Telescope has been studying gamma rays on the sky since 2008 and has created a complete map of the sky in gamma rays. The surface composition of a planet can be studied using gamma ray instruments — the MESSENGER mission to Mercury carried a gamma ray spectrometer.
Multiple Wavebands
To fully understand an object, we ideally want to look at in every type of light that it emits. For many object, this can include all types of radiation, from radio waves to gamma ray. An example of this is shown in Figure 8 for the Crab Nebula:

Understanding Radiation
Some astronomical objects emit mostly infrared radiation, others mostly visible light, and still others mostly ultraviolet radiation. What determines the type of electromagnetic radiation emitted by the Sun, stars, and other dense astronomical objects? The answer often turns out to be their temperature.
At the microscopic level, everything in nature is in motion. A solid is composed of molecules and atoms in continuous vibration: they move back and forth in place, but their motion is much too small for our eyes to make out. A gas consists of atoms or molecules that are flying about freely at high speed, continually bumping into one another and bombarding the surrounding matter. The hotter the solid or gas, the faster the motion of its atoms or molecules. The temperature of something is thus a measure of the average motion energy of the particles that make it up.
This motion at the microscopic level is responsible for much of the EM radiation on Earth and in the universe. As atoms and molecules move about and collide, or vibrate in place, their electrons give off EM radiation. The characteristics of this radiation are determined by the temperature of those atoms and molecules. In a hot material, for example, the individual particles vibrate in place or move rapidly from collisions, so the emitted waves are, on average, more energetic. And recall that higher energy waves have a higher frequency. In cooler materials, the particles have lower energy atomic and molecular motions and thus generate lower energy waves.
Blackbody Radiation and Wien’s Law
To further understand the relationship between temperature and light (EM radiation), we consider a type of ideal object called a blackbody. A blackbody absorbs all light that hits it; none of the incoming light is reflected away or passes through the object. The object heats up and gains energy; the object then loses this energy by emitting light at all wavelengths (recall that light is a type of energy). In other words, the object cools off until it reaches the same temperature as its surroundings — this is called thermodynamic equilibrium — and it does this by converting the energy it absorbed into energy of motion that is radiated in a specific way (this radiated energy is called thermal or blackbody radiation). A glowing ember of coal cools by radiating energy until it reaches the same temperature as its environment.
Any dense, solid object that has a temperature emits blackbody radiation; this includes people, animals, stove tops, light bulbs, stars and planets. For example, the Earth absorbs EM radiation from the Sun, heats up, and then emits radiation as mostly infrared light. Note that any objects that reflect light, such as a book with a red cover, are not blackbodies. Similarly, if light passes through the object, as with a glass table, it is also not a blackbody. In that respect, the Earth is not a perfect blackbody, since clouds and other particulate matter do reflect some sunlight.
No object in nature is a perfect blackbody but many opaque objects behave like a blackbody so it is a very good approximation and we can use some fairly simple math to learn more about the object. As mentioned above, blackbody radiation is not emitted at just one wavelength or one part of the EM spectrum, but covers all wavelengths. At first this may sound strange — since humans act like blackbodies, does that mean that our bodies emit dangerous X rays and gamma rays? No, that is not the case (I don’t have X ray eyes) and any blackbody emits the most intense radiation at one particular wavelength. Humans have a typical temperature of 98.6°F (or 310 K) and emit the most intense radiation at 9.3 microns (an infrared wavelength, meaning we radiate heat!). The peak wavelength of the radiation that a blackbody gives off depends only on its temperature. This means two very different objects with the same temperature emit identically with the same wavelength of peak intensity. The Earth is just a little bit cooler than a human at 288 K, and its most intense radiation is at 10.1 microns. This relationship between the temperature of a blackbody and its peak wavelength is called Wien’s Law and is:
[latex]$$ {\lambda_{\rm max} = \frac{ 0.0029 }{T} \rm{~m ~K}$$[/latex]
where the wavelength is in meters and the temperature is in K (the constant 0.0029 has units of m × K). You can easily verify λmax for a human at 310 K: (0.0029 m K)/(310 K) = 9.3×10-6 m = 9.3 microns.
The thermal radiation emitted by any blackbody shows a similar shape in the intensity of light at different wavelengths. These shapes are called blackbody curves or thermal energy curves. Figure 9 shows this general shape for blackbody curves for objects of different temperatures. The shape is similar for all temperatures but notice that the intensity for each blackbody curve peaks at a different maximum wavelength.
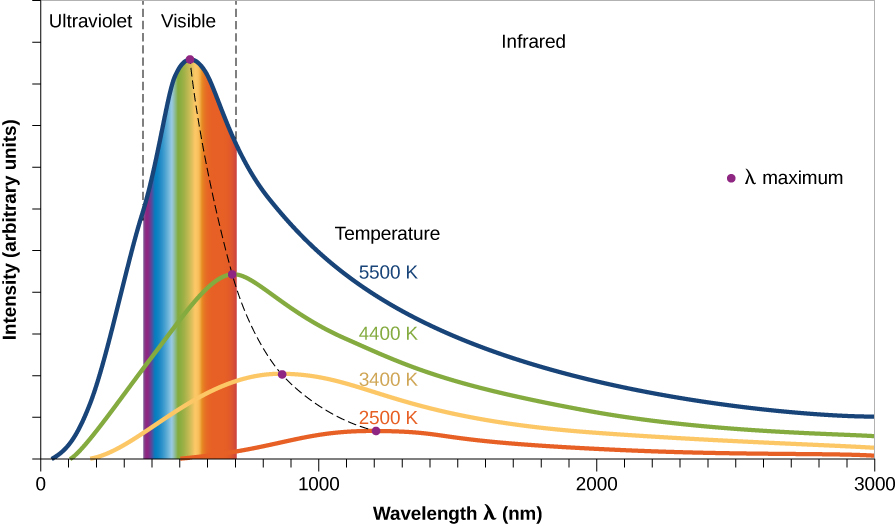
Notice in Figure 9 that the curves show that, at each temperature, the blackbody objects emit radiation at all wavelengths (all colors) but that the most energy is emitted at a peak wavelength. Physically, this peak corresponds to the average speed of atoms or molecules inside the object, which is a manifestation of its temperature.
The hotter the object, the shorter the peak wavelength — the object at 5500 K has a shorter λmax (530 nm) than the object at 2500 K (which has λmax of 1160 nm and is in the infrared portion of the EM spectrum). It makes sense, then, that hot objects give off a larger fraction of their energy at shorter wavelengths (higher energies) than do cool objects. You may have observed examples of this rule in everyday life. When a burner on an electric stove is turned on low, it emits only heat, which is infrared radiation, but does not glow with visible light. If the burner is set to a higher temperature, it starts to glow a dull red. At a still-higher setting, it glows a brighter orange-red (shorter wavelength). At even higher temperatures, which cannot be reached with ordinary stoves, metal can appear brilliant yellow or even blue-white.
We can use these ideas to come up with a thermometer for measuring the temperatures of stars. Because many stars give off most of their energy in visible light, the color of light that dominates a star’s appearance is an indicator of its temperature. If one star looks red and another looks blue, which one has the higher temperature? Because blue is the shorter-wavelength color, it is the sign of a hotter star. (Note that the temperatures we associate with different colors in science are not the same as the ones artists use. In art, red is often called a “hot” color and blue a “cool” color. Likewise, we commonly see red on faucet or air conditioning controls to indicate hot temperatures and blue to indicate cold temperatures. Although these are common uses to us in daily life, in nature, it’s the other way around.)
What about the Sun? The Sun has a surface temperature of 5800 K so Wien’s law immediately tells us that λmax is 500 nm. Which corresponds to green light. But the Sun doesn’t look green, it looks yellow or white! What’s going on?! This makes sense when you consider that the Sun is also emitting red light and blue light; these all mix together as a nearly white color. Pure purple stars are also never seen for similar reasons — the blue and violet mix into a more deep blue color.
C0lor Temperature
Different wavelengths (or frequencies) of light correspond to different colors. But what exactly is color? Is it a property of an object, like its size, or is it something that our brains perceive? Our eyes receive light, which is sent to the brain for processing. When we look at an object, we are seeing the light that is reflected off that object. If there is no light in the room, then we do not see anything at all. When light strikes an object, some of the light is reflected and some of it is absorbed. Human eyes have evolved to see visible light; some other animals, such as birds, can see ultraviolet light! Photoreceptors called cones in the retina of our eyes are sensitive to red, blue, and green light. In that sense, every color can be broken down into a combination of red, blue, and green. This is why television only needs those three colors to accurately simulate reality. In low light conditions, rods in the retina take over and are only sensitive to one color; hence, we see shades of gray.
The Sun emits white light, which contains all colors. As an example, let’s consider what happens when sunlight strikes a house painted red. The white light hits the red house, and only red light is reflected to our eyes; all of the other colors are absorbed by the paint molecules. Pigments are substances that selectively absorb very specific wavelengths of light, leaving only the desired wavelength of light reflected.
How does the color emitted by an object relate to its temperature? Wien’s law gives a mathematical relationship for this and shows that the temperature of a blackbody is inversely proportional to the wavelength of the light emitted. As a more visual example, consider a piece of metal being heated up. First it will turn a dull red color, then orange to white, and eventually it becomes blue when it is hottest. The scale is shown in Figure 10, where the temperatures are in Kelvin.

Light bulbs are designed with color temperature in mind. This is likely a familiar concept to photographers when selecting back lighting for a shoot. For a “candlelight” type background, a bulb of around 2000 K will be best, while a “natural daylight” background is best achieved with a bulb at 4500 K. Most fluorescent light bulbs in classrooms are around 5000 K while those in a library will be closer to 3000 K.
Luminosity and Brightness
Wien’s Law shows that blackbodies, like stars, emit the most intense radiation at a specific wavelength, λmax. What exactly is this intensity a measure of?
Luminosity is the total amount of energy that an object (like a star) puts out each second. It has dimensional units of energy per second. In the same way that a 100 W bulb will always put out 100 Watts whether we are standing close or farther away, the luminosity of a star does not depend on our distance from it.
However, astronomers do not measure luminosity directly with a telescope; they measure brightness: the luminosity that is intercepted by a detector such as a photographic plate or a digital camera. If you imagine a spherical surface – a bubble – around a star, then the luminosity is the integrated (total) light from the surface of that bubble. The brightness, which is the luminosity per unit area, decreases as the surface area of the spherical volume increases. This is the same phenomenon that happens with expanding balloons. The balloon has a certain amount of material, usually latex or rubber. Analogous to luminosity, that amount of material is constant, no matter how much air is in the balloon. However, as the balloon expands, that constant amount of material is stretched over a larger surface area. The walls of the balloon get thinner and the amount of material per unit area decreases. The luminosity of a star is constant. The brightness that we measure depends on whether we are “up close” or far away from the star.
This is shown in Figure 11, where the light from a star with luminosity L spreads out into spheres of increasing surface area as it travels away from the star. At a distance d from the star, we can measure the brightness ($B$) by dividing the total power emitted by the star (L) by the surface area of the sphere that the light has now spread into:
[latex]B = \frac{L}{4 \pi d^2}[/latex]
This idea—that the apparent brightness of a source (how bright it looks to us) gets weaker with distance in the way we have described—is shown in Figure 11 below. At point 1, the light is concentrated into one box. By the time the light reaches point 2, which is twice as far as point 1, it is now spread out into four squares.
Concept Check: Brightness and distances of stars
You observe two stars, named Sol-2 and Sol-3, that have the exact same luminosity as the Sun (this means they have the same temperature, radius, and luminosity as the Sun). You measure the brightness of both stars with the same instrument and find that the light from Sol-2 is twenty-five times brighter than the light from Sol-3. Which star is closer to the Earth and by how much? Explain your reasoning.
Show Answer
Ans: Sol-2 is five times closer than Sol-3. Brightness drops as the distance squared, so the ratio of the distances to Sol-2 and Sol-3 is given by [latex]\sqrt{B_{Sol2}/B_{Sol3}}[/latex] or [latex]\sqrt{25}[/latex] = 5.
Let’s consider the luminosity of the Sun and the amount of energy from the Sun that reaches the Earth. This will be important to know when we study exoplanets and want to know how much light from the host star reaches the exoplanet. The luminosity of the Sun is 3.9×1026 W — in other words, it emits the same amount of power as 3.9×1024 100 W light bulbs (or 39 trillion trillion 100 W bulbs!). As the light travels away from the Sun, it is spread out more and more, as all of that light needs to cover spheres (bubbles) that have greater surface area. The distance from the Earth to the Sun is 151 million km, or 1.51×1011 m. Putting this value into the brightness equation, we find that we receive 1360 W/m2 of sunlight on the Earth. That means every 1 m2 patch on the Earth, which is about the size of a standard chess board, receives 1360 Joules of energy every second. Venus is closer to the Sun than the Earth and receives more energy for every square meter, 2600 W/m2, while Mars is further and receives only 600 W/m2.
Worked Example: Calculating the energy received from the Sun
How much radiation from the Sun is received at Saturn’s moon Titan? You can assume that Titan and Saturn are at the same distance from Earth.
We can find the value by using the relationship for brightness, luminosity and distance:
[latex]B = \frac{L}{4 \pi d^2}[/latex]
Here, L is the luminosity of the Sun and d is the distance of Titan from the Sun. The distance from the Sun to Titan (Saturn) is 1.45 billion km (or 1.45×1012 m).
B = (3.9×1026 W)/(4 π (1.45×1012 m)2) = 14.8 W/m2
This makes sense — Saturn is almost 10 times further from the Sun than the Earth (Earth is 1 AU and Saturn is 9.57 AU), so the value should be significantly lower than Earth’s. [In fact, you could also find this value by taking the ratio (1/9.57)2 and multiplying by 1360 W/m2]
Show mathematically that the Earth receives 1360 W/m2 from the Sun.
Show Answer
The only difference here is the distance: now it is the distance from the Earth to the Sun, which is 151 million km.
B = (3.9×1026 W)/(4 π (1.51×1011 m)2) = 1361 W/m2
Stefan-Boltzmann Law
It is also apparent from Figure 9 that an object at a higher temperature emits more power at all wavelengths than does a cooler one. In a hot object (the taller blackbody curves in Figure 9), for example, the atoms have more collisions and give off more energy. In the world of stars, this means that hotter stars give off more energy at every wavelength than do cooler stars.
We can also describe our observation that hotter objects radiate more power at all wavelengths in a mathematical form. If we sum up the contributions from all parts of the electromagnetic spectrum, we obtain the total energy emitted by a blackbody. What we usually measure from a large object like a star is the energy flux, the power emitted per square meter. The word flux means “flow” here: we are interested in the flow of power into an area (like the area of a telescope mirror). It turns out that the energy flux from a blackbody at temperature T is proportional to the fourth power of its absolute temperature. This relationship is known as the Stefan-Boltzmann law and can be written in the form of an equation as
[latex]F = \sigma T^4 [/latex]
where F stands for the energy flux (in units of watts per square meter), T is given in Kelvins, and σ (Greek letter sigma) is a constant number (5.67×10-8 W/m2 K-4).
Notice how impressive this result is. Increasing the temperature of a star would have a tremendous effect on the power it radiates. If the Sun, for example, were twice as hot—that is, if it had a temperature of 11,600 K—it would radiate 24, or 16 times more power than it does now. Hot stars really shine away a tremendous amount of energy.
Key Concepts and Summary
The energy of light is our messenger about the universe. Different colors of light are simply different wavelengths and different wavelengths of light contain different amounts of energy. The longest wavelengths in the electromagnetic spectrum are radio waves and these have the lowest energy. The shortest wavelengths are high energy gamma rays. Unsurprisingly, the visible band of light (where our brain interprets different wavelengths as different colors) matches the key energy output of the Sun – we evolved to optimally navigate this range of energies. By observing the universe with detectors that are sensitive to different energies of light, we can learn about the energy output and the peak temperatures of the objects we detect. Because the brightness of a star or other celestial object decreases with distance, a measurement of distance is needed to back out luminosity (energy per second).
Review Questions
Summary Questions
- What is energy? Describe two different kinds of energy and give examples of each.
- What does it mean to say the energy is “conserved”?
- How are the frequency and wavelength of light related to each other?
- What is a photon?
- Which property of light determine how much energy a photon has?
- What are the seven main parts of the electromagnetic spectrum? For each band (part), give an example of a source of that type of radiation.
- How does the type of light emitted by an object depend on its temperature?
- What is the difference between the brightness of an object (such as a star) and its luminosity?
- How does the total amount of energy emitted differ for hot and cold objects?
Activities
- Understanding blackbody radiation. Open the simulation at https://phet.colorado.edu/sims/html/blackbody-spectrum/latest/blackbody-spectrum_en.html.
- The default is set to the temperature of the Sun. Click on the “labels” box to show different parts of the EM spectrum (UV, visible, and infrared). What part of the EM spectrum has the most intense light from the Sun.
- Now set the thermometer to the temperature of the star Sirius. The y-axis now needs to be rescaled to see the value for the peak intensity, Adjust this by using the zoom out button. Once you can see the peak, click on the “Graph Values” box. What is the wavelength of the peak intensity light for Sirius?
- Energy flux. Calculate the solar flux (in W/m2) at the planet Mercury.
ability to do work
electromagnetic radiation
the general law that total energy is constant in any process; energy may change in form or be transferred from one system to another, but the total remains the same
energy of motion
stored energy associated with a position in space
a measure of the average kinetic energy of many atoms or molecules
energy associated with different positions near a gravitating body
energy stored in chemicals due to bonds between atoms
energy associated with the mass of an object according to Einstein's equation E = m c^2
the reaction between two nuclei fusing together to become a heavier nucleus
radiation consisting of waves propagated through regularly varying electric and magnetic fields and traveling at the speed of light
The speed at which all types of light travel; 300,000 km/s
a particle of light that carries energy
