Appendix C: Units of Measurement
In Appendix A we looked at a new way to count and think about numbers and in Appendix B we learned how scientific notation that can represent numbers big and small. Soon, we will use this system to aid us in calculation, but attention is best paid now to the practical uses for these numbers. We have already seen the utility of being able to characterize the amounts of rabbits or stars that we may end up with in our new counting system, but this leads us to a more profound question: what are the things that are possible to count?
This is the place where pure mathematicians and scientists part ways. Mathematicians sometimes prefer not to worry too much about what can be counted or calculated, instead, it is the patterns, calculations and the numbers themselves that interest them. Scientists tend to be more interested in the idea of counting or assigning numbers to something. This begs the question, “What are the somethings that are possible to count?”
For a scientist a number is somewhat meaningless when devoid of context. Science teachers scold their pupils to “remember to label your units” for this reason. Five hundred and twelve is not enough; the value should instead read 512 rabbits. The numeral 512 indicates what quantity of rabbits you have. "Rabbits" is the unit of measurement and they have well-known properties that we can argue over, but hopefully we come to the consensus as to how many of them we have. This is the fundamental feature of measurement: a sharing of information that, with enough care, can be regenerated by anyone who has the right tools. Later we might measure (count) 1022 stars.
Hopefully, we can agree without too much controversy that we can measure rabbits and stars, but if we start to make an exhaustive list of all the possible things that we can count, we’ll never make any progress. That’s why over hundreds of years and continuing to the present day, the community of scientists has worked on a system to exhaustively describe the basic building blocks of reality that we can observe and measure. As with many community endeavors, there is an institution we can point to which sets the standard who collectively decides what these basic building blocks of all of reality (as far as we can tell) are. This is the obscure, but monumentally powerful group known as the International Bureau of Weights and Measures who curates the standard agreed-upon “Système International d’Unités” (SI) measurement system. This measurement system is based on the more general, and more famous, metric system that emerged in France during its Revolution.
What are the basic SI building blocks of reality? One way to answer this question might be to ask a chain of questions modeled after a child’s stereotypical curiosity. Find a thing and ask “What is that made out of?” When you get an answer, ask, “And what is that made out of?” Repeat.
Starting with rabbits or stars, for example, we will eventually happen upon the fact that both of these wildly different things are made out of the same stuff: atoms. Remarkably, there is a pretty limited variety of atoms available in the universe, so it is natural to think about how we might go about measuring, that is, counting these things.
How do we count atoms? Chemists do it by recognizing that typically an unfathomably gigantic number of them have to be in close proximity before we as human beings can recognize their existence. Coincidentally, the number required is relatively close to the order of magnitude of the number of stars in the observable universe we quoted earlier. The name for this gigantic number is the mole. This number was first estimated by the French chemist Amedeo Avogadro, and is therefore sometimes called after him, “Avogadro’s Number”. It is approximately
1 mole = 6 × 1023
which is only 60 times larger than the number we quoted for the stars in the observable universe. There are some scientists who dedicate their lives to making as precise as possible a measurement of this number, the only SI unit that is merely a number. You as you can have any number of rabbits, stars, etc., it’s possible to conceive of a mole of rabbits, stars, etc., but considering it is such a huge number, usually people only talk about moles of atoms or molecules since anything much bigger than that rapidly becomes intractable for human consideration (or absurdly non-existent — to have a mole of rabbits would imply having a population of rabbits with roughly the same mass as the entirety of planet Earth).
The word mole derives from a Latin word referring to a small amount of “mass” as it is meant to describe a quantity of things like atoms or molecules that have such tiny masses that you need a molar level of them in order to measure them. What exactly is a quantity of “mass”? Answers to this question are subject to ongoing investigation, and there are still deep mysteries as to why and how things in our universe with mass end up with that property. The base unit in SI for measuring mass is the kilogram, but linguistically, it is cleaner for our purposes us to refer to the gram as a fundamental unit of measurement. The reason that SI relies on the kilogram is because it is an amount that is easier for a human being to roughly distinguish, a kilogram being approximately the mass of a large textbook, for example, while a gram is the mass of one to a few paper clips.
The definition of the standard for mass, the kilogram, was actually revised in May 2019. Up until then, the kilogram was arbitrarily defined as the mass of a hunk of metal kept in a vault in Paris. Problematically, the actual mass of that hunk (or, indeed, any hunk of metal) changes over the decades due to natural processes. This means that there have been tiny shifts in the world’s mass measurement system that have added up to increasingly problematic annoyances for scientists trying to make the most precise measurements possible. After May 2019, the kilogram was defined using a technical definition that we will now take some time to explore.
The first step to get to the new SI definition of mass is to accept as fundamentally true Albert Einstein’s most famous equation,
E = mc2
a statement that posits that mass (m) is a form of energy (E) if you take mass and multiply it by the speed of light (c) squared (c2). This is a relationship that has been tested under a wide variety of circumstances, confirmed both on Earth all the way to observations of the furthest reaches of the Universe. We will deal more with the idea of speed of light in a bit, but for now you can treat c2 as a constant value that allows us to translate between mass and energy rather like an automated translator might allow you to convert a word in one language to that of another. Thinking of equations like this as definitions or translations will be an ongoing theme in our development of calculation skills.
With mass and the speed of light on one side, the next question we need to answer is “What is energy?” Unfortunately, this question does not have an easy-to-come-by answer, but fortunately many people have an intuitive sense of what energy is that function fairly well as a stand-in until we can get to a more rigorous foundation. The new SI definition will standardize the amount energy used to define the kilogram by declaring it to be the amount of energy discovered by Maxwell Planck contained in a fundamental particles. What is a fundamental particle? These are the true basic building blocks of matter. Atoms, you are probably aware, can be broken down into smaller subatomic particles. Some of these particles can be broken down even further. But there does seem to be a bottom to this division and that bottom is characterized by the standard model of particle physics which lists a zoo of fundamental particles which cannot be broken down more than they are already broken down. As the rudiments of quantum mechanics were developed, it became clear that fundamental particles seem to behave quite a bit differently from the hunks of matter we see at human scales.
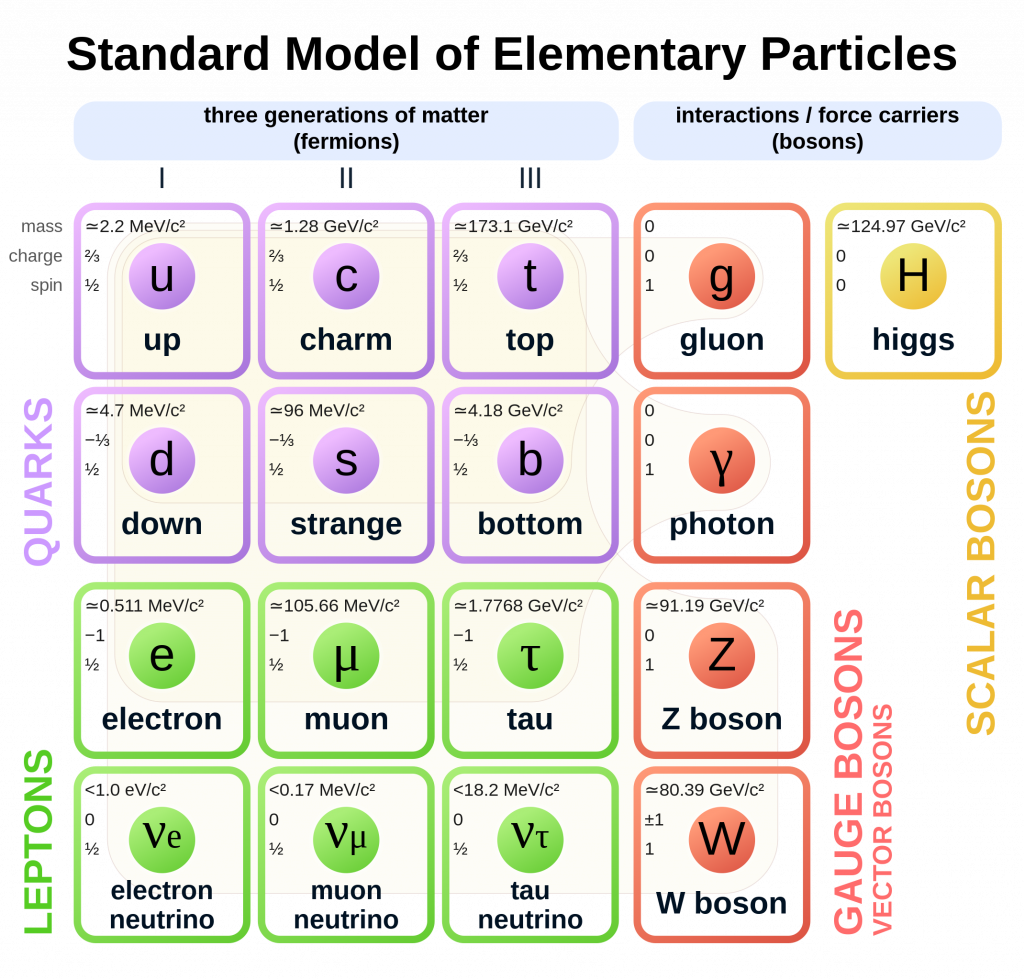
The energy of a fundamental particle is completely defined by a particle’s characteristic frequency, or in simpler terms, an aspect of a particle that exhibits a repetition in time. Mass then is just the equivalent amount of that energy divided by the constant c2. The kilogram is the equivalent mass to the energy contained in approximately 2 × 1035 photons of light that coming from the yellowish sodium vapor lamps still used to light many streets.
The frequency-dependence of phenomena that determine the kilogram give us another basic observable feature of our universe: time. Rather like mass, time is something of an ongoing mystery for scientists as to what precisely it is, and the International Bureau of Weights and Measures maintains a definition that is standardized by the number of repeated events that occur in a particular atom. The assumption is that every atom in the universe is physically identical and the processes that spontaneously occur within them happen with the same frequency regardless of where or when you find them. Lest you think scientists lazy, these assumptions are tested and verified within increasingly precise thresholds of uncertainty. You can, if you wish, even make a career out of scrutinizing this.
This allows us to define the SI base unit of time which is the second. Like the mole and the kilogram, the second is a scale that is easy for a human being to grasp and estimate conceptually.
We also know something about how time interacts with other observable features in our universe, and, in particular, time is intimately connected to space through the surprisingly more fundamental concept of the speed of light. Before exploring this, however, we need to review a simple mathematical definition of speed that we introduced in Chapter 1. In English, we define speed to be the rate at which a distance is traveled in a certain amount of time. This can be rewritten using the language of mathematics as an equation that translates between two concepts. Speed, on the one hand, and distance per time, on the other, are the same thing:
speed = distance/time
For the purposes of our explorations of the universe as whole, there is a very particular speed that we are interested in considering — the speed of light. Einstein made it clear, and it has been subsequently verified, that the speed of light does not change regardless of how we observe it. This is a unique feature that the speed of light has, all other velocities are dependent on how exactly you measure them. For example, the Earth is traveling around the Sun at a certain speed, but if you try to measure this speed by observing the distance the ground beneath your feet has traveled, you will measure the speed of the Earth to be precisely zero. This is a perfectly legitimate measurement because you are traveling along with the Earth, and the speed you measure depends on the speed you are traveling. If you could step outside of spaceship Earth, you could observe and measure the speed the Earth is zipping around the Sun (we will, in fact, calculate this later on). The dependence that a measurement of speed has on the speed of the observer was also noticed by Galileo Galilei contemplating the fact that it did not seem like the Earth was moving even though his telescope observations seemed to indicate otherwise. All motion, Galileo reasoned, was relative and different measurements of the same object taken from so-called “reference frames” moving at different speeds will measure different speeds. By contrast, the speed of light is observed to always be the same regardless of how, when, where, or who is doing the measurement. This is why we were able to treat c2 in Einstein’s most famous equation as being a constant. The International Bureau of Weights and Measures also uses the constancy of the speed of light to define the standard length, as we will now demonstrate.
Consider using some of the skills you may have happened upon in an algebra class to rewrite our last mathematical statement as
speed × time = distance
This kind of game is played all the time by people who hope to do novel calculations. The procedure is roughly as follows:
- Take a known definition (equation)
- Manipulate it using rules of algebra
- Use the newly manipulated statement to provide a new insight.
In the case of our rewriting the definition of speed, what we have done is discover a way to define distance. If we have a known time (e.g., second) and a known speed (e.g., that of light), we can multiply them together to define a distance. Such units are called light-units and they are worth an exploration before we move on. Light-units can be identified because they always start with the word light- appended with the particular time. This is shorthand for multiplying the speed of light by a time to get a distance. As light travels very quickly (in fact, it is the fastest speed that exists), light-units derived from most human-scale times are enormous. Thus, the light-second ends up being approximately the distance between the Earth and the Moon. Longer stretches of times yield even more monstrous distances. The large number of seconds in a year gives a sense for how much bigger the most famous light-unit, the light-year, is. There are the same number of light-seconds in a light-year as there are seconds in a year. We will spend some time trying to describe this distance later on, but suffice to say that as vast as it is (no spacecraft has ever traveled that far away from Earth), a light-year does not extend even as far to the next nearest star.
The SI system defines its length standard based on a light-unit, but it uses a much shorter time than one second in order to arrive at the standard length: the meter. The meter conforms to our normal goal of finding a base unit that is scaled roughly to sizes accessible to humans. Indeed, most human beings are between one and two meters. This definition of the meter was set in 1983 to roughly conform to historical definitions of the same, for the longest time it was defined using a standard metal rod kept in that same Paris vault alongside the standard kilogram.
The final quantity we will carefully investigate how to measure is temperature. The temperature standard is derived from the commonly used Celsius scale which sets, under the approximate conditions of the Earth’s atmosphere at sea level, zero degrees to be the temperature that water freezes and one hundred degrees to be the temperature that water boils. Most of us are familiar with the possibility for temperatures to go below zero. For those growing up in a cold climate, this is often how children are first introduced to negative numbers. The choice of where zero lies on the scale is arbitrary, and while frozen water at first might seem reasonable, there is actually a temperature that is much more convenient to set to zero. To find it, consider that temperature is really a characterization of the random motions of small particles. As atoms and molecules move faster, the temperature of the substance they make up increases while slower movements correspond to lower temperatures. Given this realization, it becomes possible to calculate a temperature where all particles stop moving entirely. This temperature, that for reasons that are beyond the scope of our discussion here, is impossible to reach in any laboratory environment, is approximately 273 Celsius degrees lower than the freezing point of water.
Since you cannot move more slowly than not moving at all, this is the floor for temperature below which it is impossible to descend. This temperature is called “absolute zero”, and it is mathematically convenient to start our temperature scale at this point. If we do this, we recover the SI definition for temperature: Kelvin (K). Given that a difference of one Kelvin is the same as one degree Celsius, it is straightforward to switch back and forth between them:
Temp in K = Temp in °C 273
Water freezes at 273 K. It boils at 373 K.
The SI system has two more base units which we will not find much occasion to use. Briefly, the standard unit of electric current is known as the ampere, but typically called “amps” by most electricians. Finally, the standard unit of luminous intensity, known as the candela, is now fairly obsolete as most people who measure light are comfortable with measuring how much energy is produced.
You can find a summary of our exploration of base units in Table 1. Notice that there are three greyed out; these are the units that we will not be referring to much from here on out.
Table 1: Base units and abbreviations
| Quantity | Base Unit | Abbreviation |
| length | meter | m |
| time | second | s |
| mass | gram* | g |
| temperature | Kelvin | K |
| number | mole | mol |
| electric current | Ampere | A |
| luminous intensity | candela | cd |
*Although kilogram is the SI base unit, for linguistic purposes it is better to think of the gram as the base unit for the sake of consistency.
At this point, you have enough information to start calculating conversions between many different units. For example, knowing that the prefix c = centi = 10-2, it becomes straightforward to write:
1 centimeter = 1 cm = 10-2 m
= 1 meter/100
All are equivalent statements. Using a bit of algebra, we can multiply both sides of the above equation by 100 yielding the (perhaps more) familiar result:
100 cm = 1 m
This is a fact taught in the science classrooms of grade schools the world over. Many times, teachers will request their students memorize it, but I think that’s the wrong approach. Rather, it is useful to think of the two parts of centimeter as being multiplied by each other, the centi and the meter. After seeing that, the definition becomes something that you can write down with ease, even if you had never heard of such a measurement. This linguistic and mathematical interplay uses the machinery of mathematics to construct quantities at the full range of scales we discussed previously. For example, combining the prefix micro with the base unit meter reveals the new unit micrometer that is, straightforwardly
100 μm = 10-6 m
Or, in plain English, a micrometer is one millionth of a meter. This is the approximate size of many bacteria.
