Optional Supplementary Chapter: An Expanding Universe
The big picture
Hubble's Law
In 1929, Edwin Hubble published a now-famous paper in the Publications of the National Academy of Science titled, "A Relation between Distance and Radial Velocity in Extragalactic Nebulae.'' As mentioned in the previous chapter, this work showed that M31 and M33 were beyond the known boundaries of our galaxy. In this paper he included a Table of data (reproduced below) showing distances, r, and radial velocities, v, to a couple of dozen "extragalactic nebulae,'' objects that we now understand to be other galaxies.
The "radial'' velocity is the component of velocity along our line of sight to an object. We defer a discussion of how the galactic velocities were measured to the chapter on spectroscopy, but for now, trust us... measuring radial velocities of galaxies is bread-and-butter astronomy.

Hubble sorted the galaxies by distance and immediately noticed a correlation: the more distant galaxies generally had larger radial velocities than closer galaxies. It was also clear that most galaxies - especially those at large distances - are moving away from us (by convention, positive velocities recede from us and negative velocities approach us). A few scientists of the day had already predicted this result as a critical test for a Big Bang.
Hubble plotted up his data and derived the best-fit linear velocity-distance relation. There is some scatter in Hubble's diagram. Some of this was the result of errors in the data, particularly the distances to galaxies. However, our Milky Way is one of a few dozen galaxies in what we call the Local Group. Galaxies in clusters are gravitationally bound and have orbital velocities that are larger than velocities from the expansion of the universe. Some of the velocities of galaxies in the Local Group (like the Andromeda Galaxy) are directed toward us -- those galaxies have negative velocities. Hubble's law really applies only to distant galaxies beyond the Local Group.

The speed with which galaxies are moving apart is called the recession speed. Let's think about what this linear relation between distance and recession speed means. Imagine that Galaxy A is initially at a distance d, and Galaxy B is initially at a distance 2d. Now, let enough time pass so that Galaxy A is at a distance 2d. If the expansion of space is constant everywhere, then Galaxy B will have moved to a distance 4d in that same time interval. Speed is distance divided by time; since Galaxy B travels twice the distance of Galaxy A in the same time interval, it must be traveling at twice the speed. When the expansion of the universe is constant, distance is proportional to recession velocity.
Concept Check
Can you think of how it might be possible to deduce the age of the universe from Hubble's data?
At first glance, it is tempting to conclude that the universe is expanding away from us - that we are the center of the universe. In fact, there is nothing special about our place in the universe. From the perspective of observers in every galaxy, most other galaxies seem to be receding. Indeed, alien astronomers in other galaxies have probably already published these same results, showing the relation between the distance and velocity of other galaxies. Like Hubble, they will know that they are not at the center of the universe.
The linear relationship between distance and recession velocity in Hubble's diagram (above) is expressed by a simple equation:
[latex]v = H_0 d[/latex]
The astute reader will immediately recognize this as the equation of a straight line: Here, H0 is the slope of the line and the y-intercept is zero. This equation says that the recession velocity of a galaxy is proportional to its distance. The constant of proportionality, H0, is called Hubble's constant. Mathematically, it is the slope of the line in the velocity-distance relation. The units of H0 are physically meaningful: they have units of speed per distance (typically, km/s per megaparsec, Mpc). Assuming that Hubble's constant is really constant (i.e., not changing over time), then once this value is determined, you can measure the velocity of a galaxy (with spectroscopy) to derive its distance. Galaxies with larger velocities are farther away. So, Equation 1 is a powerful way to estimate distances to other galaxies. But, keep in mind the chicken and egg problem - we had to measure velocities and distances for some galaxies to derive the Hubble relationship. Once that was done, we were able to lean on the linear model to find distances to other galaxies.

The Hubble constant tells us something rather surprising. The units of 1/H0, (or distance / velocity) are time, and this "time'' is none other than the age of the universe. It is incredible that we can calculate the slope of the line in Hubble's data and solve for the age of the universe. The only rookie mistake has to do with the units - make sure that the speed (distance per time - usually km/s) and distance (usually Mpc) are converted to the same units so that distance really cancels out. And then, you will want to convert to more useful units than seconds: years or billions of years.
So, to recap, Edwin Hubble measured distances to the nearest galaxies, proving that they were outside of the Milky Way. He measured the velocities of other galaxies and found a correlation between distance and recession speed, providing observational evidence that the universe is expanding, and yielding an estimate for the age of the universe. This work provided a resolution to Olbers' paradox: the universe is not infinitely old (we can calculate its age), and because it is expanding, the light from stars in the most distant galaxies has been redshifted out of the optical bandpass (a concept we will discuss more in later chapters). Hubble's work changed our perspective of our place in the universe, and astronomers honored his contributions by naming a space observatory after him: the Hubble Space Telescope (HST) has been a workhorse telescope for the community since the mid-1990's.
We started with a presentation of Edwin Hubble's observations of the expanding universe because it was intuitively easy to understand. However, the Belgian priest George Lemaitre deserves a lot of credit for pioneering modern cosmology. In 1927, two years before Hubble's famous paper, Lemaitre published a paper with the rather wordy title: "A homogeneous universe of constant mass and growing radius accounting for the radial velocity of extragalactic nebulae." We now know Lemaitre's model as "Hubble's law" but it was Lemaitre who worked out the theory of the expanding universe with pencil and paper, based on Einstein's theory of general relativity. He proposed that the recession velocity of galaxies (extragalactic nebulae) could be explained by this expansion, and he derived the first estimate for the rate of expansion, which is now known as the Hubble constant, H0. Lemaitre gets extra credit for persisting in the face of a harsh critic; Einstein himself reportedly told him: "Sir, your calculations are correct, but your physics is atrocious." In the 1930's the idea that the universe was expanding was an extraordinary claim, and it would require extraordinary evidence (to borrow a phrase from Carl Sagan) before this theory was accepted.
The Cosmic Microwave Background Radiation
Thirty years later, a surprising observation further cemented the idea that the universe started with a Big Bang and has been expanding ever since. Bell Telephone Labs in New Jersey had built a sensitive radio antenna designed to send signals across long distances. The antenna became obsolete when telecommunication satellites were launched in 1962. Two Bell Lab employees with backgrounds in radio astronomy, Arno Penzias and Robert Wilson, realized that the antenna would be an excellent radio telescope if it were used as a receiver instead of a transmitter. As soon as they began using the telescope, they picked up background noise, like static in a radio, with a specific wavelength of 7.35 centimeters. No matter where they pointed the antenna, they measured the same signal. The isotropy of the signal suggested that the source was extragalactic; but what was causing it?

Meanwhile, just down the road from Bell Labs at Princeton University, four cosmologists (astrophysicists who study the origin of the universe) were thinking about observational tests that could support their theories about the early universe. They reasoned that if the matter-dominated universe started with a Big Bang, it must have been accompanied by a tremendous burst of high energy radiation. As the universe expanded and cooled, that primordial energy would have stretched to longer-wavelength, lower-energy radiation. This radiation should permeate the entire universe so that today it would be a low-energy isotropic cosmic background radiation. The Princeton astrophysicists had already drafted a paper predicting that the cosmic background radiation should be detectable today at microwave energies. The Princeton and Bell Labs scientists worked collaboratively and published side-by-side papers presenting the theory and the observations: "The Cosmic Background Radiation" by Dicke, Peebles, Roll and Wilkinson and "A Measurement of Excess Antenna Temperature at 4080 Megacycles per Second" by Penzias and Wilson. The cosmic microwave background (CMB) radiation has traveled for almost the entire history of the universe. We are immersed in the CMB today - there are about 400 photons from the CMB in every cubic centimeter of the space around us.
The discovery of the cosmic microwave background radiation by Penzias and Wilson was so transformational that it earned them a Nobel prize in physics in 1978. It also motivated the launch of not one, not two, but three space satellites to refine measurements of the CMB. Each new mission provided higher spatial resolution and more precise information about the energy fluctuations in the CMB. The first of these satellites, the Cosmic Background Explorer (COBE) was launched by NASA in 1989 to map the microwave background of the universe. The COBE mission measured energy of the CMB radiation and showed that it was consistent with a blackbody (more about this later, but a blackbody emits a distribution of energy that is characteristic of its temperature) radiating with a peak temperature of 2.73 Kelvin.
The fact that the universe has approximately the same temperature in all directions is profoundly important. It implies that the entire universe was once in thermal contact - the entire universe sprang into existence from a tiny point. Importantly, there are also very subtle deviations from this uniform temperature and that fact is equally profound. This suggests that there were small fluctuations in the spatial map of the CMB temperature that are linked to slight density variations (1 part in 100,000) in the early universe. These density variations were the seeds for the large scale structure of the "normal" matter in the universe: galaxies, galaxy clusters, and vast empty voids. The anisotropy of the CMB is important enough to re-emphasize: if the universe had been perfectly homogenous and smooth, it would not be possible for galaxies, stars, or us to exist today.

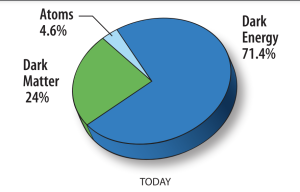
COBE was the precursor for a second NASA mission called the Wilkinson Microwave Anisotropy Probe (WMAP). The map of the sky from WMAP obviously has higher spatial resolution, but it also provided a more precise resolution of temperature variations. By fitting models of expansion to the WMAP image, astronomers were able to nail down the age of the universe as 13.77 billion years, and they quantified the composition of the universe: ordinary atoms (4.6%), dark matter (24%), and dark energy (71.4%).
The European Space Agency (ESA) launched Planck, the third major space probe to study the CMB. Planck provided the most precise image ever of the distribution of matter in the universe on large and small scales. The data from the ESA Planck mission provided a more precise measurement of the age and composition of the universe and showed that the first stars formed 370,000 years after the Big Bang - later than previous estimates. Planck also derived an independent measurement of the Hubble constant, H0 = 67, which disagrees with measurements derived from the recession velocity of galaxies. This suggests that either astronomers are missing some physics in their cosmological models or the data have as-yet unrecognized measurement uncertainties.

The Hubble measurement was so important that it has been re-examined by several astronomers, including Wendy Freedman and her colleagues in 2001. Compare the range of distances and recession velocities from their work, reproduced below, with the original Hubble data. The exact value for the Hubble constant, H0, is still a topic of active research and intense debate.

The Early Universe
Astrophysicists have used observations of the expanding universe and the CMB radiation along with standard models of physics to extrapolate back to roughly 10-43 seconds after the birth of the universe. We do not yet have physical data to tell us what existed before that time, and standard models of physics cannot describe this era. But, it seems likely that the universe existed in a state of extremely high pure energy. Quantum energy fluctuations would have transformed this pure energy into particles with mass. The problem is that those particles should have emerged in equal measures of matter and antimatter: quarks and anti-quarks, electrons and anti-electrons (or positrons). When a matter and antimatter particle come into contact, they destroy each other, producing electromagnetic radiation with the same energy that corresponds to the mass of the particle. The universe might have existed for a very long time before the Big Bang, bubbling back and forth with some equilibrium between pure energy and particle-antiparticle constituents. However, as far as we can tell (and luckily for us), the antimatter counterparts are missing from our universe today except when they are briefly created in particle accelerators. Indeed, understanding what happens to anti-matter is one of the key research questions of physicists working now at the CERN Large Hadron Collider.
Immediately after the Big Bang, the cosmic clock began ticking and all of space popped into existence with a temperature of about 10 billion degrees and with unimaginable pressure. At this stage, the universe was a soup of fundamental particles: electrons, protons, neutrons, and quarks. As the seconds ticked by, protons fused together to form the nuclei of helium and lithium atoms.
The nuclei for all of the hydrogen atoms and most of the helium and lithium atoms that exist in the universe today were formed in the first three minutes after the Big Bang. After three minutes, the universe had expanded and cooled so that the conditions for nuclear fusion no longer existed. The cosmic web of space and time continued to expand and cool, and after 300,000 years, the temperature of the universe was about 3000 Kelvin, cool enough for electrons to pair with the atomic nuclei and form the first three elements in the Periodic Table. As the universe expanded, the density of energy decreased. The number of photons is approximately constant, and the energy of a photon is defined by its wavelength. So in a universe where the energy density has decreased, the wavelength of light stretched from the highest energy gamma rays at the time of the Big Bang, to the low energy microwaves that make up the CMB today.
There are four types of "stuff" in the universe: baryonic matter (you, me and everything we see), radiation (energy), dark matter, and dark energy. Since we don't know what dark matter or dark energy are, how would you characterize our ignorance about the universe? How can energy and mass be mathematically related as "stuff" in the universe?
The density variations that we see in the CMB maps provided the seeds for structure. As higher density pockets began to collapse over the 300,000 years, the first stars formed, and on larger scales, over millions of years, the first galaxies formed. Our model of the CMB allows us to create a model of the earliest moments of the universe that ends with the structure of the universe as we know it today. The CMB observations also help to constrain the fractional mass and energy constituents of the universe. We are in the strange position of knowing that most of the universe is comprised of mass and energy that we can't really describe - we simply call it "dark matter" and "dark energy."
In Caleb Scharf's well-written book "Gravity's Engines," he discusses the idea of a "fair sample of the universe." Imagine that you have a giant bag that contains a representative and proportional sample of all the mass-energy "stuff" in the universe. Shake the bag so that everything is well mixed and then scoop out some of this stuff. What would you be holding? Hydrogen? Photons? Exotic particles like neutrinos? It's a good bet that you would have scooped out dark energy (this is a thought experiment - dark energy is not something that can actually be scooped up) with perhaps a smattering of dark matter. As the pie chart in Figure 8 shows, something like 71% of the universe is comprised of dark energy, and dark matter makes up another 24%. If you study chemistry, you are studying less than 5% of the stuff in the universe. It turns out that the part of the universe that we encounter in our lives is rare stuff.
There are cross checks for the beginning-to-end model that is derived from the Cosmic Microwave Background: it must also agree with the cosmological models that are derived from observations that look back from the present time. In other words, we can start with the CMB observations and model the evolution of the universe forward in time. Or we can start with observations of the local, present-day universe and observe more distant galaxies (i.e., look backward in time) to calculate the Hubble constant and the expansion of the universe. Those two methods: "from the beginning to the present time" and "from the present time to the beginning" should have predictions and postdictions that match.

The agreement is good to about 10%, but when we account for all of the physics that we think we understand, that agreement should be much better. In other words, there is a cosmological controversy. The CMB model predicts a universe with too little matter to match observations today. The resolution to this disagreement is that the Hubble Constant appears to be changing over time. Looking back to a time when the universe was half its current age, the expansion rate was slower - about 80% of the current rate.
Dark Matter and Dark Energy
In discussing the Big Bang and the expansion of the universe, we focused on the formation and evolution of the stuff that we can see. But, as noted above, astronomers have learned that there is more -- so much more -- to the universe. We just don't know what it is. The existence of dark matter was first predicted by Fritz Zwicky - a Swiss physicist working at the California Institute of Technology, who was by all accounts both a prescient thinker, and quite a character. Zwicky obtained photographs of the Coma galaxy cluster and calculated the gravitational mass that must be keeping the cluster bound together -- that calculation suggested that the cluster mass was 400 times greater than the luminous material. His results were not widely accepted at the time.

Then, in the 1960s, Vera Rubin and Kent Ford studied the velocities of stars in spiral galaxies and found that the stars at the outer edges of the galaxy were moving as fast as the stars closer to the center. That observation does not fit with Newtonian physics unless one invents the idea that there is "dark matter" - material that cannot be seen but that exerts a gravitational effect on objects that we do see. Rubin proposed that a spherical distribution of dark matter existed in galaxies - an idea that was initially viewed with great skepticism.
The existence of dark matter was also observed in elliptical galaxies. Sandy Faber and Robert Jackson measured a correlation between the orbital speeds of stars in elliptical galaxies and the mass of the galaxy. Faber and Lin later helped to lift the curtain on the properties of dark matter, ruling out fast-moving neutrinos and concluding that dark matter could still be another type of slow-moving sub-atomic particle. Many candidates for "dark matter" have been proposed, from free-floating planets to weaking interacting massive particles (WIMPS). WIMPS are winning out as the favored candidate for dark matter, but we have not detected them yet. If WIMPS are the answer, their discovery may await detection with a clever new instrument with higher precision. Zwicky deserves credit for proposing the existence of dark matter. Rubin and Faber obtained confirming data that convinced the astronomical community that there really was more to the universe than just the stuff that we see.

We know that the universe is expanding, but is the expansion constant? Was it faster in the past, and decelerating now? Or was it expanding more slowly in the beginning, but now the expansion rate is accelerating? The second possibility, a decelerating universe, would mean that the universe is headed for a big crunch. The third possibility -- an accelerating expansion -- is only possible if there is a mysterious energy driving the expansion. A "mysterious energy source" seems the least likely; yet that is what the empirical evidence suggests. The expansion rate of the universe is increasing and we have no idea why. Astronomers refer to the mysterious energy source that is accelerating the expansion of the universe as "dark energy."
The Future Universe: Expanding Out of Sight
The expansion of the universe is accelerating and most of the universe is disappearing. We can currently observe light that has been traveling for less than 14 billion years. However, the expansion of the universe has carried those distant galaxies away from us during this 14 billion year timespan. As a result, the universe is larger than 14 billion light years in size. Current models of the universe estimate that the universe is 90 billion light years across.
The expansion rate of the universe is so fast that light leaving a galaxy that is more than 14 billion light years away will never catch up to us. Those distant galaxies have disappeared from the observable universe. The size of the observable universe is 14 billion light years but the radius of the actual universe is about 45 billion light years; we have lost the ability to see 97% of the galaxies in the universe.
Want to know more: The Missing Universe
Assume that the universe is spherically shaped. If the density of galaxies is constant throughout the entire universe, then we can calculate the fraction of galaxies that reside in the "observable" universe as the ratio of a sphere with a radius of 14 billion light years to a spherical volume with a radius of 45 billion light years:
[latex]\frac{V_{\rm observable}}{V_{\rm total}} = \frac{\frac{4}{3} \pi (14)^3}{\frac{4}{3} \pi (45)^3} = 0.03 = 3\%[/latex]
Only 3% of the galaxies in the universe are possible to observe. Because of the finite speed of light, the other 97% have forever receded from our view.

The accelerating expansion of the universe means that the fraction of the universe that is unobservable to us in the future will continue to increase. Our local cluster of galaxies will remain gravitationally bound with the Milky Way. However, the rest of the universe is disappearing from sight.
