1 Sizing Up the Cosmos
To approach the subject of astrobiology – specifically, of exploring possibilities that other life exists beyond the Earth – it is worthwhile to ponder the size and age of the cosmos. In this grand scheme, when and where did life on Earth first appear? The moment when the first life appeared is not precisely known, but several lines of evidence provide compelling clues for the timing of the rise of life on Earth.
Learning Objectives
By the end of this chapter, you will be able to:
- Explain the idea of the “cosmic calendar” and the timing of key events for life
- Express small and large numbers using powers of ten
- Describe the range of sizes for objects in the universe
- Explain light units such as light years and light seconds
- Describe how parallax can be used to estimate the distance to an object
Our Place in Time: The Cosmic Calendar
The universe emerged at the moment of the Big Bang, 13.8 billion years ago. This is our starting point for time. Key events since this moment, including the formation of our galaxy and our solar system, can be identified in a memorable way by compressing all of time into one calendar year. This idea for the “cosmic calendar” was first articulated by astronomer Carl Sagan. On this cosmic calendar (Figure 1), each month represents a little over a billion years. Each day covers a span of around 40 million years. The very first stars and galaxies form in late January, and our home galaxy, the Milky Way, forms in early March. Our solar system comes on the scene in early September, and the first life on Earth probably formed by mid- to late-September.
Life starts as very simple cells and gradually evolves into more, with the first multicellular life appearing in November, and the first plants on December 20th. Primates, including humans, appear on December 31. In fact, modern humans show up on December 31, at 11:52 PM, which is on the order of the real-time equivalent of hundreds of thousands of years ago. In the bottom panel of Figure 1, which zooms in on the last 60 seconds on December 31, we see that all of modern science, including the development of both the telescope and microscope in the 17th century, happen in the last second at 11:59 PM.

There are a few ways to think about this time frame. On one hand, technologically advanced humans on Earth are newcomers. Humans have been sending out radio waves for less than one cosmic second. However, considering that the first life to appear on Earth took only a few cosmic weeks to form, perhaps the initial formation of life on other worlds will be a relatively speedy process. When considering just how many planets there are in the cosmos, it is tempting to think that the odds of life existing on at least one other planet are good.
Our Place in Space
Space also emerged at the moment of the Big Bang, and it has been expanding ever since. Contemplating the size of the cosmos can seem mind-bending but we can ground ourselves by starting with some size comparisons of more familiar objects. When comparing the sizes of two objects, a good first step is to be clear as to what is being compared, as the word size can mean different things — length and volume, for example, are do not measure the same thing. Here, let’s compare the length of some different objects, where the length is the distance from one end to the other end. Of course not all objects are symmetric so you may need to be more specific about how you are defining length, depending on what is being compared. For example, bacteria come in different shapes, such as rods, spheres, and spirals. In specifying a bacterium’s size, you would need to be clear about the start and end points of the measurement. In astronomy, galaxies also come in different shapes – ellipsoids, spirals, and irregular shapes – so it is important to know which dimension (say left to right or top to bottom) the length is referring to.

Units of length are important to consider. Lengths and distances are one-dimensional measures and are expressed in units such as meters or miles. Of course, the length of any object can be expressed in any units: what’s important is that the objects being compared have the same units. Let’s compare the size of a grapefruit and a bacterium. The length of a typical grapefruit is around 10 inches, which is the same as 25.4 centimeters (cm), 0.254 meters (m), 0.000254 kilometers (km) or 0.000158 miles. These are all equivalent measures, and it is a matter of convenience when choosing units. When directly comparing two measurements, all that matters is that the units chosen for the grapefruit are the same as those for a bacterium. We know that bacteria are very small, and a typical size is reported in units of micrometers (μm), where the prefix micro indicates 0.000001 meters. So, we can compare a grapefruit and a bacterium using meters (m): a grapefruit is 0.254 m and a bacterium is 0.000001 m. Clearly, the grapefruit is larger than the bacterium, and we can find exactly how much larger by dividing the two sizes: (0.254 m)/(0.000001 m) = 254,000. Dividing the two sizes (or taking the ratio) shows that the grapefruit is 254,000 times larger than the bacterium. We could still use a way to simply our notation, as it’s easy to accidentally leave off one of the zeroes in the size of the bacterium. That’s where “powers of ten” notation becomes useful.
Powers of Ten
Scaling to the largest sizes we will consider, a galaxy is a vast collection of stars that are held together by gravity. The length of a typical spiral galaxy, like the Milky Way, is about 1,000,000,000,000,000,000,000 meters (m), or a billion trillion m. This is a huge number, with 21 zeros after the one (this length is called a sextillion meters). The number may seem more intuitive when expressed as one billion trillion, as billion and trillion are familiar values that show up in our daily life (for example, billionaires are often in the news, and although no trillionaires yet exist, we intuitively know how much money they would have). When writing these numbers the prefixes M and G are sometimes used, where M stands for a million or the prefix “Mega” and G for a billion or the prefix “Giga”.

One additional way to express these number is by using powers of ten. A million expressed in powers of ten is 106, since there are 6 zeros. Similarly, the Milky Way’s size can be written as 1021 m. There is also a prefix for 1021, called zetta and abbreviated by a Z. The Milky Way’s size can be expressed as 1021 m, 1 Zm or 1 sextillion m. This link to the National Institute of Standards and Technology lists the common prefixes that we use. In this table, we see that a yoctosecond is a very small measure of time – it is a mere septillionth of a second or 10-24 s. We will make regular use of powers of ten notation in this course, as we will be dealing with immensely large and small numbers.
In the context of comparing such a wide range of phenomena as this subject warrants, a good first step is to estimate the order of magnitude of the scale of an object. The easiest way to do this is to write the measurement in scientific notation and consider only the exponent. Notice that we need to identify the units of measurement as well as the order of magnitude to avoid ambiguity.
To get a better feel for very large and very small numbers in nature, the following film, created by Charles and Ray Eames in the 1970s, explores the very largest and very smallest numbers using powers of ten. Note that since the creation of this film, scientific advances have aided in the more complete understanding of the largest and smallest scales so that we now have more exacting probes of the largest scales and the smallest scales shown in the film. Our maps of galaxy clusters and investigations to the observable limits of our universe have improved to the extent that we can accurately identify the distribution of millions of galaxies while our understanding of the standard model of particle physics has been confirmed down to the centers of atomic nuclei.
Copyright © Eames Office, LLC. All rights reserved.
The smallest measurable sizes bring us inside the nucleus of an atom, where subatomic particles called protons, with a size of just 10-15 m, are found. On the largest scale, the size of the observable universe is estimated to be about 1026 m. These are such vastly different sizes it is hard to even imagine comparing them, but it can be done very simply. The question of “how many times larger” one object is compared to another object can be found by dividing the two numbers: 1026 m/10-15 m = 1041 (for a review on working with powers of ten and scientific notation, please see Appendix B). The answer tells us that the observable universe is 1041 times larger, or “41 powers of ten,” larger than a proton. This can also be stated by saying that the universe is 41 orders of magnitude larger than a proton.
This type of analysis is powerful. Compared to the entire size of an atom, the nucleus is about 10,000 times smaller (104, or 4 orders of magnitude). This tells us that an atom – the fundamental building block of matter – is mostly empty space. The universe, it turns out, is also filled with huge voids of empty space.
Concept Check: Exponential sizes
Storage devices come in different sizes, and a small flash drive might have 64 MB of space and a large drive could have 500 GB. The small flash drive has 64 million bytes of space, where a million is 1,000,000 – one with six zeros. The “M “in MB stands for the prefix Mega, meaning million, and “B” is the abbreviation for bytes. Note that G is the prefix Giga, meaning billion.
To compare the size of a 512 MB flash drive to a 64 MB flash drive, this can answered in one step by dividing the two sizes: 512 MB/64 MB = 8. The 512 MB is eight times larger than the 64 MB drive. To state it another way, you would need eight 64 MB drives to equal one 512 MB drive. Notice that the answer, eight, has no units (or, we say is “dimensionless”). This makes sense – since both sizes are in MB, we compared “apples to apples”.
If the question asked how many times larger a 512 GB drive is compared to a 64 MB drive, you would need to make the units agree before dividing the numbers. Do this!
Show Solution
There are a few different ways to approach this: you could convert from GB to MB, from MB to GB, or convert both units into B. Let’s convert 512 GB into MB, so that both quantities will have the same units:
512 GB × (103 MB/1 GB) = 512×103 MB
Now, we can divide the two quantities since they are both in MB: (512,000 MB/64 MB) = 8000
It takes eight thousand 64 MB flash drives to equal one 512 GB drive.
If the conversion directly from GB to MB was not clear, we can do this in two steps:
512 GB × (109 B/1 GB) × (1 MB/106 B) = 512×109×10-6 B = 512×103 MB = 512,000 MB
Stars
The power of a star can be measured in Watts (W), just like light bulbs. The Sun’s power output is 3.8×1026 W and the power of the star Arcturus is 6.5×1028 W.
(a) How many times more powerful is Arcturus than the Sun? (b) How many times less powerful is the Sun than Arcturus?
Show Answer
(a) We can simply divide the power of Arcturus by the power of the Sun to find this:
(6.5×1028 W)/(3.8×1026 W) = 171
(b) 0.0058 or (1/171)
Density
Another important measure in the context of life and other worlds is density. The density of a planet, for example, will be important in assessing whether that planet has a rocky surface, like Earth, or an entirely gassy composition, like Jupiter.
The density of an object tells us how much stuff fits into its available space. Or, to be more specific, how much mass fits into its volume. You cannot tell the density of an object just by its mass or just by its volume – you need to consider both quantities together. For example, two planets could have the exact same volume and have the same size and shape in a picture, but their densities depend on what kind of matter is inside. A tennis ball and a billiard ball have roughly the same volume, but the tennis ball is filled with air and is much less dense than a billiard ball of the same size. By definition, the density ($\rho$) of an object is found by dividing its mass by its volume and is often reported in units of g/cm3 (since mass can be measured in grams and volume is three-dimensional and is measured in cubic units, such as cm3): $$\rho = \frac{M}{V}$$
Table 1 lists some common densities:
| Substance | Density | Astronomical Object | Density |
| hydrogen | 0.00009 g/cm3 | Earth | 5.5 g/cm3 |
| air | 0.001 g/cm3 = 1 kg/m3 | Sun | 1.4 g/cm3 |
| water | 1 g/cm3 | Saturn | 0.7 g/cm3 |
| iron | 8 g/cm3 | white dwarf | 700,000 g/cm3 |
| lead | 11 g/cm3 | neutron star | 7 × 1014 g/cm3 |
| gold | 19 g/cm3 | Universe | 9 × 10-30 g/cm3 |
Concept Check: Density
(a) Looking at Table 1, how many times more dense is a neutron star compared to the planet Saturn?
(b) Of the elements shown in Table 1, gold has the highest density. Is gold the heaviest element? Look this up!
(c) Which object has a higher density (or do they have the same density): a 1 milligram piece of gold or a 50 milligam piece of gold?
Show Answer
(a) 1015 or 1 quadrillion
To find how many more times dense a neutron star is compared to Saturn, take the ratio of the two densities:
(density of neutron star)/(density of Saturn) = (7 × 1014 g/cm3)/(0.7 g/cm3) = 1015
(b) osmium is the densest element
(c) They have the same density! Density is an intrinsic property of an element and doesn’t change with the size of the piece.
Light Units and Speed
To explore the chemistry and possible biology of other worlds, ideally we would send humans there to run experiments. Humans have been to the Moon to collect rocks, and there are currently several rovers that are controlled from Earth analyzing rocks and soil on the surface of Mars. There are plans to send humans to Mars in the next decade or two. Why not send humans sooner? There turn out to be many challenges to physically traveling beyond the Earth, but the distances involved are foremost.
We are familiar with long distances on Earth. The distance from NYC to Sydney, Australia is about 10,000 miles (16,000 km) and a typical jet flies at a speed of 575 mph, so this flight takes over 17 hours. How about the distance from Earth to the Moon or Mars? The Moon is around 240,000 miles (384,000 km) away and Mars is over 200 million miles from Earth. In 2020, the Perseverance spacecraft travelled at 24,600 mph to Mars and still took about 7 months to get there. The amount of time it takes to travel somewhere is the distance divided by the speed you are traveling, or:
time = (distance)/(speed)
If you are traveling to a place 30 miles away at a steady speed of 60 mph, then it takes you (30 miles)/(60 mph) = 0.5 hour to get there.
Concept Check: Distances, speed and time
If it takes 18 days for a rover moving at a steady speed to travel a distance of 6 km, how fast was the rover moving?
Show Answer
speed = (distance)/(time)
speed =(6 km)/(18 hours) = 1/3 km/hr = 0.33 km/hr
In fact, this is the maximum speed that the Perseverance rover can reach.
Perhaps you can just travel at faster speeds to get someplace far, like Mars, more quickly? While this idea works well for speeds on Earth (and hence we have supersonic jets and bullet trains), there is a limit to how fast anything can travel. This cosmic speed limit is called the speed of light, and nothing can travel faster. In fact, only light, which has no mass, can travel at the speed of light; any object with mass can never reach this speed due to the effects of Einstein’s theory of special relativity. So, the fastest possible way to reach a distant world is to send light. This may not seem very helpful at first, but light can contain information – think about radio or TV signals – so this is a potential way to send communications to distant worlds.
How long would light take to reach Mars? The speed of light, which is denoted by the symbol c, can be expressed in any units, such as km/hr, mph, or feet/s. Two common choices are m/s and km/s:
c = 300,000 km/s = 3×105 km/s = 3×108 m/s
(For comparison, a variety of speeds that we may encounter in astrobiology are listed in Table 2.) The distance to Mars when it is closest to the Earth is 55 million km. Using the simple relationship for time, distance, and speed, we arrive at an answer of 183 seconds. That’s fast – only about 3 minutes! And definitely faster than the 7 months the Perseverance spacecraft took. This way of thinking about distances, times, and the speed of light is so useful, in fact, that astronomers often use light units to express distances. The Sun is 93 million miles away from Earth. If we do the same calculation for how long light from the Sun takes to reach us on Earth, it is 8 minutes. That’s about three times as long as light takes to get to and from Mars. We can now express the distances d to the Sun and Mars, in light units: dSun = 8 light minutes and dMars = 3 light minutes
| Scenario | Speed | Scenario | Speed |
| Drift speed of the continents | 3 × 10-9 m/s | Orbital speed of the Earth around the Sun | 30 km/s |
| Growth speed of human hair | 5 × 10-9 m/s | Escape speed from the Solar System (at the distance of Earth) | 40 km/s |
| Automobile | 100 km/hour = 28 m/s | Fastest human-made object | 110 km/s |
| Rotational speed of the Earth at the Equator | 1700 km/hour = 480 m/s | Orbital speed of the Sun around the Galaxy | 220 km/s |
| Orbital speed in low-Earth orbit | 8 km/s | Escape speed from the Galaxy (at the location of the Sun) | 310 km/s |
| Escape speed at Earth’s surface | 11 km/s | Speed of light = c | 3 × 105 km/s |
Worked Example: Light Units
Show that 1 light year is equal to 9.46 trillion km.
Recall that a light year is the distance that light travels in 1 year. We can use the relationship between time, distance and speed, along with unit conversions, to show this.
distance = (speed)×(time)
Here, we know the speed–the speed of light–and can express it in any units…let’s use km/s, since the answer is in units of km. In the equation below, we use 3×105 km/s for the speed. For the time, we use 1 year and convert this to seconds.
distance = (3×105 km/s)×(1 year)
distance = (3×105 km/s)×(1 year)×(365 days/1 yr)×(24 hours/1 day)×(60 min/1 hr)×(60 sec/1 min) = 9.46×1012 km
Recall that a light year is the distance that light travels in 1 year. We can use the relationship between time, distance and speed, along with unit conversions, to show this.
distance = (speed)×(time)
Here, we know the speed–the speed of light–and can express it in any units…let’s use km/s, since the answer is in units of km. In the equation below, we use 3×105 km/s for the speed. For the time, we use 1 year and convert this to seconds.
distance = (3×105 km/s)×(1 year)
distance = (3×105 km/s)×(1 year)×(365 days/1 yr)×(24 hours/1 day)×(60 min/1 hr)×(60 sec/1 min) = 9.46×1012 km
This is equal to 9.46 trillion km.
How long does it take light from the Sun to reach Saturn, in minutes?
Start with the average distance from the Sun to Saturn in km, which is 1.4 billion km.
Show Answer
Light from the Sun is traveling at the speed of light, or 3×105 km/s.
time = (distance)/(speed) = (1.4×109 km)/(3×105 km/s) = 4,667 seconds
(4667 sec)(1 min/60 sec) = 78 minutes
We can thus say that Saturn is 78 light minutes away from the Sun.
How about the closest star to the Sun? That’s a red star named Proxima Centauri, and it is staggering 40,208,000,000,000 km (40 trillion km or 4×1013 km) away. In light units, however, this distance is 4 light years. It takes light 4 years to reach Proxima Centauri. The distances in light units to some nearby astronomical objects are shown in Figure 4. Light units are very convenient for expressing distances to stars that have intriguing planets orbiting them, as this tells us how long a radio signal would take to arrive at the star system. Also, light units remind us that we have a way of looking into the past! Notice in Figure 4 that the Andromeda galaxy is 2.5 million light years away. This means that light from Andromeda takes 2.5 million years to reach us, and that consequently we are seeing Andromeda as it looked 2.5 million years ago. This gives astronomers a way to see how the oldest galaxies in the universe, that are more than 13 billion light years away, looked when they were very young!
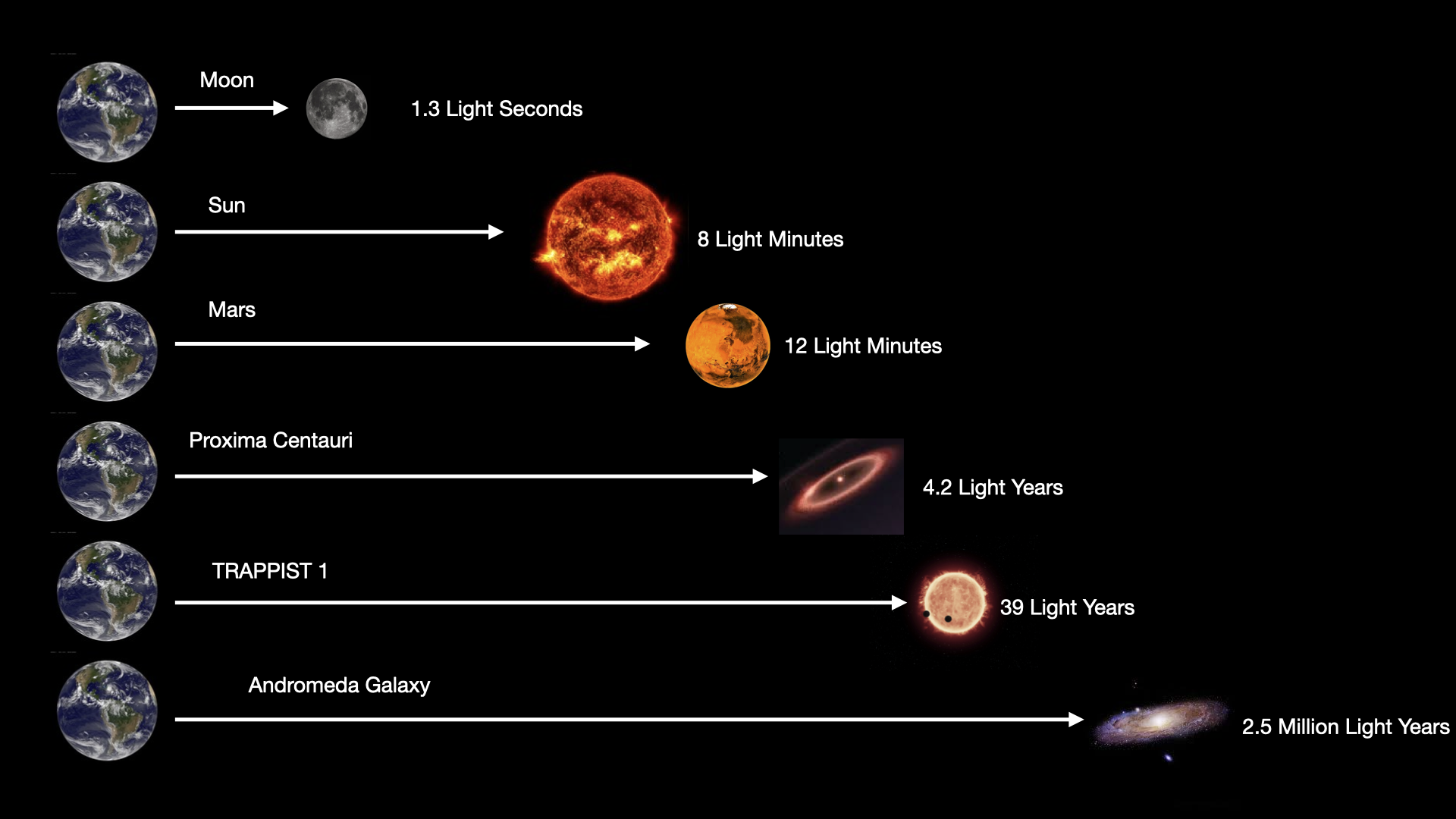
Concept Check: Distances
In Figure 4, the distance of 12 light minutes from Earth to Mars is actually the average, as the distance from Earth to Mars varies from 3 light minutes to 22 light minutes (at the furthest distance, it is on the opposite side of the Sun compared to Earth). When Mars and the Earth are at their closest distance, how long does it take light from the Sun to reach Mars?
It may help to make a sketch of the alignment of the Sun, Mars and Earth when Mars and Earth are closest to each other.
Show Sketch and Answer

The left panel shows the alignment of the Sun, Earth, and Mars when Mars is closest to the Earth. The time for sunlight to reach the Earth is 8 light minutes and the time for light to travel from Earth to Mars is 3 light minutes at closest approach. Thus, the total time is 8 light min + 3 light min = 11 light min
Other units of distance in astronomy
If you look up the distance to an astronomical object, the units will vary. For example, the distance to the star Vega might be reported in light years or parsecs — it is 25 light years away which is the same as 7.8 parsecs. The Oort cloud surrounding our solar system is 50,000 AU away. Let’s introduce these units as well.
Astronomical Units
When reporting distances within solar systems, astronomical units (AU) are typically used. One AU is defined to be the average distance from the Earth to the Sun. Mercury and Venus are closer to the Sun than the Earth and thus have distances in AU that are less than 1 AU. Saturn is at about 10 AU from the Sun and Neptune is at 30 AU.

When you read about the distance of an exoplanet from its host star, these are also reported in AU and have the exact same meaning as in our solar system. The exoplanet Proxima b orbits the red star Proxima Centauri, and Proxima b is an average distance of 0.0485 AU away from Proxima Centauri. This means Proxima b is very close to its star: it is nearly 2 orders of magnitude closer to Proxima Centauri than the Earth is from the Sun.
Parsecs
Parsecs (abbreviated pc) and light years have similar values:
1 pc = 3.26 light years
It is usually a matter of context in deciding which units to use although it is usually more intuitive for students to use light units.
The word parsec is a portmanteau of the words “parallax” and “arcsecond” and is defined as “the distance at which we have a parallax of one second.” Parallax is an angular measure, meaning it has units of degrees or radians (or arcminutes and arcseconds). The apparent shift in the direction of an object as a result of the motion of the observer is called parallax. We call the shift in the apparent direction of a star due to Earth’s orbital motion stellar parallax. The Greeks made dedicated efforts to observe stellar parallax, even enlisting the aid of Greek soldiers with the clearest vision, but to no avail. The brighter (and presumably nearer) stars just did not seem to shift as the Greeks observed them in the spring and then again in the fall (when Earth is on the opposite side of the Sun). In reality, stellar parallax angles were too small to measure with scientific instruments until the 19th century.
Concept Check: Angular Units
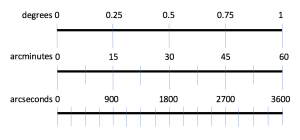
The basis for angular units is that there are 360° or 2$\pi$ radians in a full circle. Arcseconds and arcminutes are simply divisions of a degree into smaller units, where 1 degree contains 60 arcminutes (abbreviated as 60$’$) and 1 arcminute contains 60 arcseconds (abbreviated as 60$”$).
The best way to visualize parallax angles is to hold up something like a pencil at a distance of just a few inches from your nose. Now, hold up another pencil at the greatest distance that you can reach (as demonstrated below). If you wink your eyes (left then right), you’ll see that the pencil that is closest to your face appears to have a much larger shift (right to left) than the distant pencil.

We use the same principle to measure distances to stars. Stars that are close to us will have larger parallaxes than more distant stars. Winking our eyes won’t work for this measurement because the baseline (the distance between our eyes) is too small. Instead, we use the baseline of the Earth’s orbit to see apparent position of the foreground stars jump relative to the background stars.

The parallax angle is abbreviated as p . It can be shown using simple trigonometry that the distance to a star is inversely proportional to its parallax angle:
$$d = \frac{1}{p}$$
where $p$ is reported in arcseconds and $d$ is given in parsecs.
Key Concepts and Summary
The scale of space and time in the universe is so enormous that we need strategies to organize a basic understanding of where and when. The cosmic calendar re-scales the 13.8 billion year age of the universe into a “cosmic year”, effectively capturing the timing for the rise of life and the very recent appearance of modern humans. The exponential spatial scale of the universe is captured as powers of ten, to compare the smallest and largest sizes and distances. A common unit for distances is light travel time: light could travel the circumference of the Earth seven times in just one second. It takes light 8 minutes to travel from the Sun to the Earth; 4.3 years to travel from Earth to the nearest star system, alpha Centauri, and 2.5 million years to travel to the closest spiral galaxy, Andromeda. Another important distance scale in astronomy is the distance from the Sun to the Earth: 1 Astronomical Unit or 1 AU. As we look out into the universe, determining the distances to other stars is accomplished with high school level trigonometry: measuring the shift of foreground stars relative to more distant stars.
Review Questions
Summary Questions
- How does the “cosmic calendar” help in understanding when key events happened for the development of life on Earth?
- How do you compare the size (or any property) of two objects using powers of ten?
- How does the smallest size we can observe compare with the largest size? Give an example of two objects that vary by 8 orders of magnitude. How about 17 orders of magnitude?
- What are light units? Why is it convenient for astronomers to use light units when expressing distances?
- How many light years are there in 1 parsec? Describe the unit parsec and why it is named the way it is.
- How can parallax be used to estimate the distance to an object?
Exercises
- Using the speed in Table 2, how long will your hair grow in one month?
- The Voyager 1 spacecraft is traveling at a speed of 38,000 miles per hour (17 km/s). Express this speed in light years per second (ly/s). How long would it take Voyager 1 to reach the closest star to the Sun, Proxima Centauri, which is 4.3 light years away?
- There are some additional exercises using powers of ten and scientific notation here (with solutions).
the study of life in the context of astronomy, especially as it pertains to searching for life beyond the Earth.
the entirety of the physical extent of reality especially considering very distant locations
the entirety of all that exists, sometimes limited specifically to that which can be observed, or, the "observable universe".
an event that occurred 13.8 billion years ago when the universe began expanding from an extremely hot and dense primordial state
an assemblage of stars, gas, dust, and dark matter that are held together gravitationally and, as units, make up the structure of the cosmos
Objects in our local planetary system that are gravitationally bound, including the Sun, the eight planets and their moons, asteroids, comets, and other debris.
(1934-1996) astronomer and science communicator who worked on solar system science, the search for extraterrestrial intelligence, and skepticism
first identified as bright points of light in the night sky, stars are highly concentrated balls of matter, mostly hydrogen, that emit tremendous amounts of energy similar to our own Sun
the galaxy where we live
considered by many biologists to be a key feature of life, a cell contains biological material separated by a membrane
organism with more than one cell
multicellular lifeform that uses photosynthesis as its primary metabolism
class of mammals including humans, apes, monkeys, tarsiers, lemurs, and lorises often noted for their opposable thumbs
optical device used to see very distant and faint light sources
optical device used to see very small objects
The longest wavelength, lowest frequency, and lowest energy forms of electromagnetic radiation.
Fundamental force that acts between two massive objects causing them to be attracted to each other.
The size of a number to within a factor of ten. When using scientific notation, the order of magnitude can be quickly estimated by considering the exponent while the coefficient is less important.
the largest sized gravitationally bound objects in the universe
The current best understanding for how the subatomic particles are composed and interact.
The central portion of atoms composed of protons and neutrons confined by the strong nuclear force.
Positively charged subatomic particle composed of two up quarks and one down quark.
The speed at which all types of light travel; 300,000 km/s
