The Habitable Zone

Debra Fischer; Allyson Sheffield; Joshua Tan; Lily Ling Zhao

19 The Habitable Zone

In assessing the possibility that life could exist on another world, one of the first questions to ask is: “Is it in the habitable zone?”. The habitable zone around a star is the region in which the temperature on the surface of the planet would be in the proper range to allow liquid water to exist. If a planet does fall into the habitable zone around its host star, we cannot immediately conclude that life exists but it is a useful starting point in looking for other worlds that contain life.

Learning Objectives

By the end of this chapter, you will be able to:

Discuss the concept of the habitable zone around a star
Describe the habitable zone around the Sun
Explain the difference between the equilibrium and surface temperature of a planet
Compare the surfaces and atmospheres of Earth, Venus and Mars
Explain the concept of a continuous habitable zone

Defining the Habitable Zone Around a Star

One of the mantra’s in Astrobiology is “Follow the water!”. This makes sense from our Earthly perspective, since absolutely all life on Earth requires liquid water. On Earth, where there is water, there is life. Of course, other liquids could serve this same purpose in other environments, but we stay focused on liquid water for defining the habitable zone around a star.

The habitable zone around a star is the region where the temperature is appropriate for liquid water to exist on the surface of a world. Sometimes this region is called the “Goldilocks Zone,” an analogy to the fairly tale Goldilocks and The Three Bears and the “just right” temperature for porridge (not too hot or too cold – Figure 1).

NASA — Figure 1 – The habitable zone is sometimes referred to as the “Goldilocks” zone, as it is the region where the temperature is not too hot and not too cold for liquid water to exist.

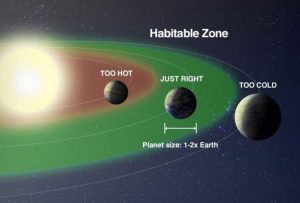
Strictly speaking, this means that a planet in the habitable zone has a temperature in the range between the freezing point and the melting point of water: 273-373 K (which is 0-100°C, or 32-212°F). While this may seem simplistic, as the presence of liquid water depends not only on temperature but on the surface pressure of a world and whether there is an atmosphere, it is a good way to begin the process of identifying potentially habitable exoplanets around another star. Other factors can then be considered to rule out the world as being habitable. For example, the Moon is in the habitable zone around the Sun but it is not a habitable world; the Moon is much smaller than the Earth and has lost all of its internal heat. While we tend to mainly think of rocky worlds as places that can harbor life — as life on Earth likely began at the liquid water-land boundary — many exoplanets that are gas giants fall into the habitable zone around their star. The first exoplanet detected around a Sun-like star, 51 Pegasi b, is actually a gas giant.

Let’s start by looking at the habitable zone in our own solar system, as shown in Figure 2. Currently, the Sun is about halfway through its life, with an age of about 4.6 billion years. Over time, the Sun will get hotter and the habitable zone around it will shift further away from the Sun — we discuss this point further in the Continuous Habitable Zone section below. Today, the Earth and Mars fall into the Sun’s habitable zone; Venus is too close to the Sun for liquid water oceans to exist on its surface — any previous liquid water has completely evaporated. The Earth is at a distance of 1 AU from the Sun. What are the inner and outer boundaries of the Sun’s habitable zone?

Cornell University/NASA. — Figure 2 – The Habitable Zone around the Sun is a distance where planets might have the right conditions for liquid water to exist on their surfaces. **Which solar system planets are currently in the Sun’s habitable zone?**

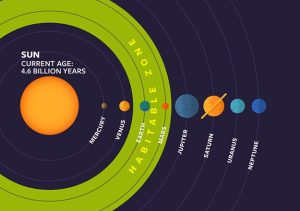
Two ranges for the habitable zone are often quoted: one is a conservative estimate, with a more narrow range of distances, and the second is the optimistic estimate, which is wider. The conservative estimate accounts for changes due to water in a planet’s upper atmosphere that can lead to a “moist” greenhouse effect, which sets in earlier than the “runaway” greenhouse effect. For the Sun, the conservative range is 0.95 – 1.37 AU, while the optimistic range extends the borders to 0.85 – 1.7 AU. Figure 2 shows the optimistic habitable zone around the Sun; the conservative estimate would not include Mars, which is 1.5 AU from the Sun.

The box below shows an example of how to estimate the boundaries for the habitable zone around any star.

Worked Example: The Boundaries of the Habitable Zone Around a Star

To approximate the inner boundary of the habitable zone around a star, we can calculate the distance from the star where the temperature is equal to the boiling point of water. The outer boundary of the habitable zone is calculated as the distance from the star where the temperature would equal the freezing point of water.

Recall from the Stefan-Boltzmann law that the luminosity (total power output) of a star is:

$L = \sigma T^4 4 \pi d^2$

where is the distance d from the star. By taking the ratio of these values and using the conservative inner and outer habitable zone boundaries for our solar system (d_inner,Earth= 0.95 AU and d_outer,Earth = 1.37 AU), we obtain the following relationships:

$d_{inner,star} = 0.95 \sqrt{L_{star}/L_{Sun}}$ AU

$d_{outer,star}= 1.37 \sqrt{L_{star}/L_{Sun}}$ AU

For example, let’s calculate the habitable zone boundaries around the star TRAPPIST-1. A quick search shows that the luminosity of TRAPPIST-1 is less than just one-thousandth of the luminosity of the the Sun: L_T-1= 0.00052 L_Sun. In one step, we can put this luminosity into the relationships above and find that the inner and outer boundaries for the habitable zone around TRAPPIST-1 are d_inner = 0.022 AU and d_outer = 0.032 AU. In our solar system, Mercury is 0.39 AU, so the habitable zone for TRAPPIST-1 is extremely close to the star compared with our habitable zone.

Questions

Calculate the inner and outer boundaries of the habitable zone around the star Pegasi 51 (this is the star that 51 Pegasi b orbits).
Calculate the optimistic habitable zone boundaries around Pegasi 51.

Show Answers

d_inner = 1.08 AU, d_outer = 1.56 AU
0.97 – 1.94 AU. Note that a luminosity of 1.3 L_Sun was used for these calculations.

Comparing Venus, Earth & Mars

Although they are very different places today, the planets Venus, Earth and Mars all started out with very similar conditions. They all formed at the same time from materials in the solar nebula, meaning that they all started off with the same compositions mixed together in a hot liquid. As these molten planets cooled, their interiors differentiated and their early atmospheres and oceans formed. The materials in the atmosphere came primarily from volcanic outgassing with some contributions possibly from impacts from comets (all three planets experienced many impacts during the Late Heavy Bombardment from 4.1 – 3.8 Gyr ago). Some materials that were outgassed include a mix of CHONS: sulfur dioxide (SO₂), hydrogen sulfide (H₂S), carbon dioxide (CO₂), and ammonia (NH₃). Note that there was no free O₂ in these early atmospheres, as oxygen will quickly bond with other elements once it enters the atmosphere. Oxygen in Earth’s atmosphere is a byproduct of life.

ESA — Figure 3 – Venus, Earth, and Mars. The planets are shown to scale, with Mars having about half the radius of Earth.

Today, the Earth’s atmosphere is dominated by molecular nitrogen (N₂) and oxygen while both Mars and Venus have atmospheres almost entirely dominated by CO₂. These differences can be explained by considering both the size and distance from the Sun of Venus and Mars.

Table 1: Comparison of Venus, Earth, and Mars. Values in the first five rows are relative to the Earth’s value.
	Venus	Earth	Mars
Mass	0.82	1	0.11
Radius	0.95	1	0.53
Distance from the Sun (AU)	0.72	1.00	1.52
Surface gravity	0.91	1	0.38
Atmospheric pressure	90	1	0.007
Main atmospheric gas(es)	CO₂	N₂, O₂	CO₂

Venus and the Earth are very close in size while Mars is significantly smaller. Table 1 summarizes the data. In terms of radius, Venus has nearly the same radius (95% Earth’s size) while Mars has about half — 53% — the radius of Earth. This means that Mars likely has already lost most or all of its internal heat while Venus may still retain internal heat to this day that can drive geological activity. The surface gravity of Venus is very close to the Earth’s (at 91%) while Mars has only 38% the surface gravity of Earth. This means that it is much easier for any atmosphere Mars had in the past to be lost to space, and this is consistent with the extremely thin atmosphere that Mars holds onto today. We devote an entire chapter to exploring the possibility of water (and life) on Mars.

It is quite possible that for the first billion years after it formed, Venus had a moderate temperature atmosphere, surface water, and perhaps even life. However, because Venus is closer to the Sun, it intercepts more energy than the Earth. Liquid water would have gradually evaporated, forming a potent greenhouse gas that trapped more solar energy, leading to a positive feedback loop that further warmed the planet, driving water out of the crust of Venus.

Ultraviolet radiation dissociates water molecules into its component atoms of hydrogen and oxygen. The Venus Express spacecraft, launched in 2005 by the European Space Agency (ESA), has measured the escape of hydrogen and oxygen (roughly in a ratio of 2:1) from the upper atmosphere of Venus. Over the 4.56 billion year lifetime of the planet, Venus has lost its water. Carbon dioxide is chemically bound in the crust of Earth rocks. However, in the presence of a hot, dry Venusian climate, carbon dioxide would evaporate out of the mantle of the planet, producing the heavy CO₂ atmosphere observed today. The current condition of Venus is the fate of an Earth-like planet that is too close to its star to retain liquid surface water.

Equilibrium Temperature

Considering that the amount of power from the Sun received by a planet should be equal to the amount of power emitted by the planet, we can calculate the equilibrium temperature of a planet (see Box 2 below for details). The equilibrium temperature of Venus and Earth are T_eq,Venus= 260 K and T_eq,Earth= 255 K. How does this compare with the actual measured values at the surface of Venus and Earth? The actual temperature at the surface of Venus is 730 K (457°C)! Venus experienced a runaway greenhouse effect, with all of its CO₂ now baked out of rocks and in the atmosphere.

The Earth’s actual surface temperature is 288 K (15°C), putting it right into the habitable zone range for liquid water. The Greenhouse effect is often portrayed in a negative way, as the increase of greenhouse gases in the Earth’s atmosphere causes the global temperature to rise and exacerbates climate change– and this is a real concern if Earth is to avoid the fate of Venus prematurely. However, keep in mind that without a Greenhouse effect the Earth would be an ice ball!

Worked Example: Calculating the Equilibrium Temperature of a Planet

To find the equilibrium temperature of a planet, we can consider the power that reaches the planet from its star and is absorbed by the planet, and the power that is emitted by the planet. This planetary energy budget is in balance so we can set them equal to each other: $P_{in} = P_{out}$

The power reaching the surface of the planet is the product of the amount of energy reaching the planet, the cross-section of the planet that receives this energy, and the fraction of this light that is absorbed by the surface. This can be written:

$P_{in} = (L_{star} / 4 \pi d_{p}^2) \times (\pi R_{p}^2) \times (1-a)$

where $L_{star}$ is the luminosity of the star, $d_{p}$ is the distance from the star to the planet, $R_{p}$ is the radius of the planet, and $a$ is a variable called the planetary albedo. The planetary albedo is a measure of how much light is reflected back by the planet, meaning it doesn’t reach the surface. This can be due to ice on the surface or in clouds. In our solar system, $a_{Earth}$ = 0.32 and $a_{Venus}$ = 0.75; Mercury has the lowest albedo at 0.12. The luminosity of the star can be written using the Stefan-Boltzmann law as $L_{star} = \sigma T_{star}^4 4 \pi R_{star}^2$ .

The power emitted by the planet is the produce of the energy flux radiated by the planet (in W/m²) multiplied by the total surface area of the planet:

$P_{out} = (\sigma T_{p}^4) \times (4 \pi R_{p}^2)$

where $T_{p}$ is the temperature of the planet.

Setting $P_{in} = P_{out}$ and solving for $T_{p}$ , we obtain the following equation for the planetary temperature:

$T_{p} = T_{star} \sqrt{R_{star}/(2 d_{p})} (1-a)^{(1/4)}$

We can rescale this relationship so that the input units are AU for $d_{p}$ and we use the Stefan-Boltzmann law to rewrite $T_{star}$ and $R_{star}$ in terms of $L_{star}$ :

$T_{p} = 278.1 (L_{star}/L_{Sun}) \sqrt{1/d_{p}} (1-a)^{(1/4)}$

Example 1: Equilibrium temperature of Venus

For Venus, we just need the distance from the Sun in AU and Venus’ planetary albedo: $d_{V}$ = 0.72 AU and a = 0.75. For the luminosity of the star, since it is the Sun, $L_{star} = L_{Sun}$

$T_{Venus} = 278.1 (L_{Sun}/L_{Sun}) \sqrt{1/0.72} (1-0.75)^{(1/4)}$ = 260 K

This is much cooler than the actual surface temperature of Venus, which has undergone a runaway greenhouse effect. To calculate the adjusted temperature that factors in the greenhouse effect, an extra term ge must be factored into the equation, which appears as (ge)^-1/4. This term varies from 0 to 1, where 1 means no greenhouse effect. Try recalculating the temperature of Venus with different values for the ge term. Which gives a good match to Venus’ actual surface temperature of 730 K? [Ans: about 0.15]

Question: Calculate the equilibrium temperature of Mars.

Show Answer

The equilibrium temperature of Mars can be found in the exact same way as for Venus: now we need the average distance of Mars from the Sun and its planetary albedo. Looking these up, we find: $d_{M}$ = 1.52 AU and has an albedo of a = 0.16 (reference: https://astronomy.swin.edu.au/cosmos/a/Albedo). For the luminosity of the star, since it is the Sun, $L_{star} = L_{Sun}$

$T_{Mars} = 278.1 (L_{Sun}/L_{Sun}) \sqrt{1/1.52} (1-0.16)^{(1/4)}$ = 217 K

Exoplanetary Habitable Zones

The discussion of the habitable so far has focused on the Sun. However, we can intuitively imagine how the habitable zone would differ for stars that are hotter and cooler than the Sun.

Thought Question: How do you expect the habitable zone to change for a star that is hotter than the Sun? Will it be closer, further, or the same distance away from the star as the Sun’s habitable zone? Will it be narrower or wider, or the same width as the Sun’s habitable zone? Now answer the same question for a star that is cooler than the Sun.

Show Answer

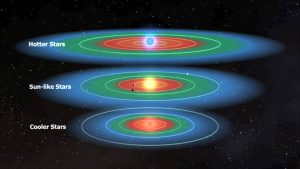
NASA/Kepler Mission/Dana Berry — Figure 4 – The habitable zone around a hot, average (Sun-like) and cool star. **What types of stars have habitable zones that are wider and extend to greater distances than the HZ for the Sun?**

As seen in Figure 4, a star hotter than the Sun (such as those with spectral types OBAF) has a wider habitable zone that is further away from the Sun. This makes sense, as a hotter star on the Main Sequence has a higher luminosity and thus more energy reaches the planet than from a cooler star. Because there is more of it, this energy can spread further before the temperature dips below the freezing point of water, so the habitable zone is wider. The same logic can be applied to the cooler star, which has a narrower habitable zone that is closer to the star.

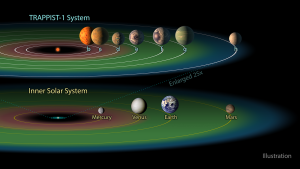
Let’s look at the habitable zone around the star TRAPPIST-1, which we considered above. You can see a nice animation of the habitable zone for TRAPPIST-1 here. The inner and outer boundaries of TRAPPIST-1’s habitable zone were estimated to be from 0.022-0.032 AU (see Box 1 above). The closeness of TRAPPIST-1’s habitable zone to the star is exemplified by seeing that the TRAPPIST-1 system needs to be zoomed in 25-times for it to be compared on the same image as our solar system.

NASA/JPL-Caltech — Figure 5 – The habitable zone around the star TRAPPIST-1. Note that we have magnified the TRAPPIST-1 system, which would entirely fit inside the orbit of Mercury in our solar system.

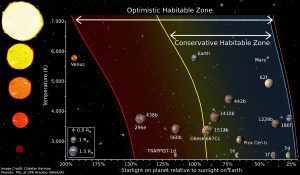
Another way to visualize the habitable zone around stars of different types (temperatures) is to calculate how much light is received at a planet. Figure 6 below shows how the intercepted starlight varies with the temperature of the host star. The brightness percentages on the x-axis are shown relative to the Earth (by definition, the Earth is 100%, so a planet with a percentage greater than 100% receives more light from its host star than the Earth does). Some known exoplanets that are around the same size as the Earth are plotted for comparison. The boundaries for the habitable zones are shown; why does the width of the HZ increase as the temperature of the star increases?

Chester Harman — Figure 6 – The amount of intercepted starlight is shown relative to that of Earth for different mass (temperature) stars. The horizontal x-axis could also be shown as distance from the star. Earth-sized exoplanets are shown for comparison.

The Continuous Habitable Zone

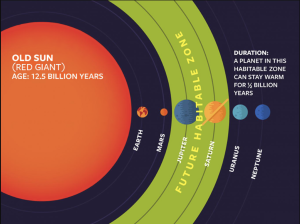
The Sun is getting more luminous as it ages. This means that over time the habitable zone around the Sun will be pushed further away, and eventually Earth will be in the “too hot” zone. This is true of all stars on the Main Sequence. A star’s brightness increases by about 0.7% every 100 million years. Since forming 4.5 billion years ago, the Sun is now 30% brighter today than it was when it started shining continuously. In about 2 billion years from now, the Sun’s optimistic habitable zone’s inner edge will be out past 1 AU, so Earth will no longer fall into this zone. Figure 7 shows how far the Sun’s habitable zone will extend once the Sun becomes a red giant star, in about 8 million years from now. Notice that Mercury and Venus have been swallowed up by the Sun at this point.

Cornell University — Figure 7 – The Sun’s HZ in 8 billion years. The HZ will no longer contain Earth and the Sun will completely engulf Mercury and Venus.

Key Concepts and Summary

The Habitable Zone is the region around a star where it is “not too hot” and “not too cold” for liquid water to exist. The boundaries of the habitable zone are set by the luminosity of the host star. For billions of years, this luminosity will be constant as hydrogen is being fused into helium in the core of the star. However, after the star burns all of the hydrogen in its core, it will evolve and begin burning an outer layer of helium. When this occurs, the luminosity of the star increases and the boundaries of the habitable zone move out. In addition to the luminosity of the star, the atmosphere of a planet can trap radiation, further warming the planet. In our solar system, the Earth, our Moon and Mars reside in the habitable zone – since we have not found life on the Moon or Mars, this shows that the concept of a habitable zone is an idealization, perhaps necessary but not really sufficient to infer the existence of life as we know it.

Review Questions

Summary Questions

What is the habitable zone around a star?
What property (or properties) of a star determine the location of its habitable zone?
What are the optimistic and conservative boundaries for the habitable zone around the Sun?
Which planets are in the Sun’s habitable zone?
What is the difference between the equilibrium temperature of a planet and its actual (measured) surface temperature? What causes these two temperatures to vary, especially in the case of Venus?
How do the atmospheres of Earth, Venus and Mars vary? What led to these differences?
How does the habitable zone around a star change as the star evolves?

Exercises

Generate the habitable zone around another star. Choose an exoplanetary system that you think could have some habitable planets. [Try http://astro.twam.info/hz/ or https://ccnmtl.github.io/astro-simulations/circumstellar-habitable-zone-simulator/]
Greenhouse effect PHeT sim: https://phet.colorado.edu/en/simulations/greenhouse-effect

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Astrobiology Copyright © by Debra Fischer; Allyson Sheffield; Joshua Tan; and Lily Ling Zhao is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.