Transit Method

By 1999, about a dozen planet candidates had been detected with the Doppler technique, and most were similar to the hot Jupiter 51 Peg b, with minimum masses of about one Jupiter mass and orbits of just a few days.  Even the astronomers working with the Doppler method were deferential in calling these objects planet “candidates” in those early days because the true mass of the orbiting companion could not be determined with this detection technique.

However, astronomers knew that if these really were planets (and not face-on stellar binary systems), about one in ten of the short-period 51 Peg b type objects would have an orbit that was oriented so that the planet would “transit” or cross our line of sight to the star. When that happens, the planet blocks some of the starlight for the few hours that it transits.

Measuring the brightness of stars is relatively straightforward, and each of the stars with 51 Peg b type exoplanets were being monitored for a possible transit. While the Doppler technique cannot determine the inclination, the data do predict when a planet will transit if the inclination is viewed nearly edge-on. If a planet transits, we know that must be close to 90° and, therefore, . In this case, the Doppler measured mass is no longer just the minimum mass; it is the total, true mass of the planet.

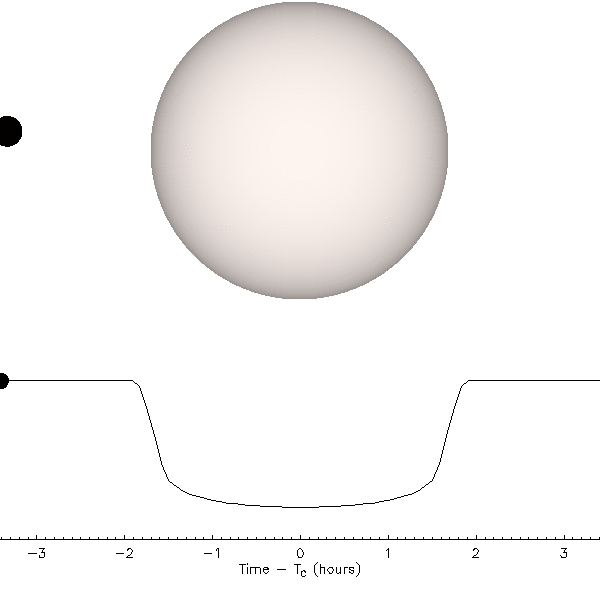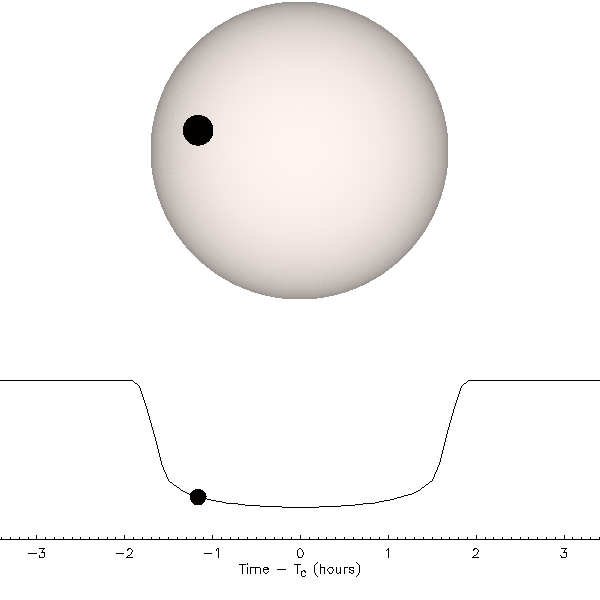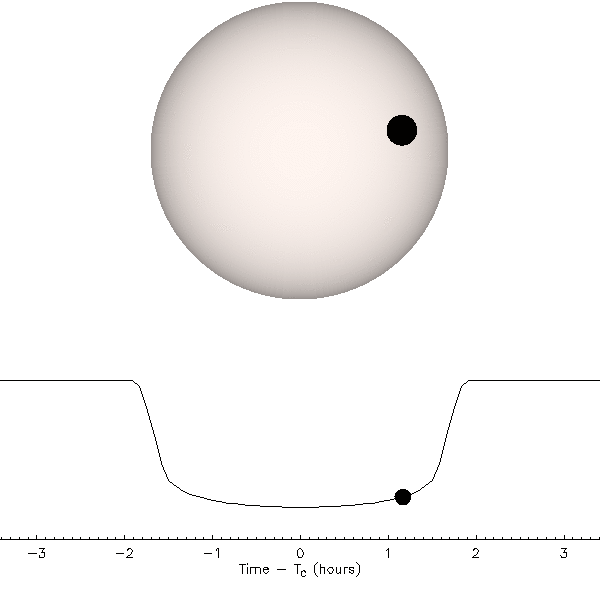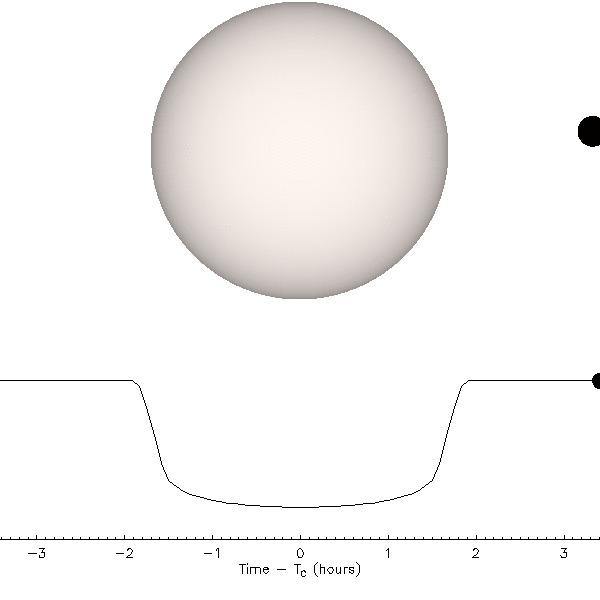
Figure 14 above illustrates what is happening. During a transit the planet passes in front of the star (top animation), and as this happens the brightness of the star decreases (bottom animation). We do not actually have pictures like the top animation because stars are point sources of light, not resolved objects. The data that we have are the time series photometry (brightness measurements) depicted in the lower animation that show a regular and periodic decrease in the brightness of the star at precisely the putative transit time (predicted by the Doppler velocity measurements). Because we cannot resolve the image of the planet (or the star), this is still an indirect detection technique. However, even astronomers sometimes take some poetic license here and say that we are seeing the shadow (or the silhouette) of the planet.

There is only one case where we can resolve the physical extent of star, and that is for our Sun. If the Earth is in the right position on our orbit around the Sun, we can see the inner planets, Mercury and Venus, transiting the Sun. This fortuitous alignment happens about 13 times a century for Mercury and fewer than 2 times per century for Venus. The video below shoes a simulation of the 2012 the transit of Venus. You will have to wait until Dec 10, 2117, to see the next transit of Venus. Can you estimate the transit depth for Venus crossing the Sun?

The first transiting exoplanet

HD 209458 b was the first star where astronomers observed a transiting exoplanet. The planet had a mass similar to Jupiter’s with a short orbital period of just a few days, and was independently detected by two teams using the Doppler method in the summer of 1999. HD 209458 b was the twelfth example of a hot Jupiter (a 51 Peg b analog) — recall that about one in ten close-in planets was expected to transit — and the planet hunters were anxiously awaiting the validation of “planet” status that a transit would bring.

In August and September 1999, the team led by Harvard graduate student David Charbonneau and Dr. Tim Brown, observed a transit at the time predicted by the Doppler velocity data. Their published data are shown in Figure 15. The ground based photometry (brightness measurements) is good enough that you can unambiguously see the transit event, but “blurring” caused by the Earth’s atmosphere caused some of the starlight to be scattered. This blurring effect is what causes stars to appear to twinkle on the night sky. The team was able to combine data from multiple transits to reduce their errors to 0.015%. This precision is very impressive, but not high enough to detect a transiting planet like the Earth with a radius that is one tenth of Jupiter. A second team, led by Greg Henry, measured a partial transit in November of that same year, and the two discovery papers were published back-to-back in The Astrophysical Journal.

(area of planet)/(area of star) =

The transit depth equation above says that the fractional change in brightness () of the star is proportional to the radius of the planet () to the star () . We measure the brightness of the star without a transit and the decreased brightness during transit. So, if we know the radius of the star, we can solve this equation to derive the radius of a planet that we cannot even see. Science is amazing!

In our everyday lives, we have a lot of experience with what artists call perspective. Objects that are closer to us look larger than objects that are farther away.  This sometimes lead to an incorrect intuition that transit depth is related to the star-planet separation since the more distant planet are “closer” to us. However, the incredible distances to the stars that we observe mean that the difference in star-planet distances within a given planetary system are negligible.

The Transit Simulator

Let’s use the NAAP transit simulator from UNL to understand how transiting exoplanets are detected with time series photometric data. The default shows a gas giant planet (see the Planet Properties box and note that the mass and radius are relative to Jupiter) orbiting a star slightly more massive than the Sun; the inclination of the system is 86.9°. Jupiter has a radius that is 11.2 times larger than the Earth’s, meaning that the Earth’s radius is 0.089 times the radius of Jupiter. What happens to the light curve (upper right) when you change the radius of the planet to Earth’s size? You can quantify the difference by looking at the value for the eclipse (transit) depth reported to the lower right of the light curve. How do you expect the light curve to change, if at all, if you lower the mass of the exoplanet?

Now let’s look at the data for the first exoplanet detected with the transit method, HD 209458 b. In the Presets box, choose this planet from the drop-down menu and click “set”. What is the eclipse depth? What is the inclination of this system? At what inclination would you no longer be able to measure the transit? The eclipse depth will show (no eclipse)” when there is no transit observed. (add show answer here, it’s 82.7°) [will also add longer activities at end of chapter]

The Kepler Mission

A decade before the first exoplanet was discovered, William Borucki, a scientist at NASA Ames Research Center in Mountain View CA, wrote a paper “The Photometric Method of Detecting Other Planetary Systems” (Borucki & Summers 1984) where he made the case for a space mission to detect planets orbiting other stars using the transit technique. It took more than twenty years of advocacy, but Borucki’s persistence paid off. The first exoplanets were discovered in the mid-1990s, heating up interest, and after the first ground-based transit discovery in 2000, the exoplanet community rallied behind Bill Borucki’s plan.

The first question in deciding whether to go forward with a space mission is: can this be done from the ground? If so, then the mission is a no-go. The justification for the space-based Kepler transit mission was the need to reach higher precision. Ground-based transit surveys could detect only 1% (0.01) changes in the brightness. The important limitations to the precision of ground-based photometry (brightness measurement) were blurring from the Earth’s atmosphere and the limited number of dark nighttime hours when the telescopes point away from the Sun. From space, the atmospheric blurring is limited and the telescope can always point away from the Sun. The higher photometric precision was demonstrated by the Hubble Space Telescope, which measures 0.1% (0.001) changes in brightness. However, a special purpose telescope was really needed that could reach even higher precision with continuous monitoring of stars.

In 2009, NASA launched the Kepler Mission, which measured 0.01% or (0.0001) changes in the brightness of the host star. Figure 16 below shows that Kepler was remarkably successful in detecting a range of exoplanets with radii down to a couple times the radius of Earth.

The specific science goal for Kepler was to determine the occurrence rate of Earth-sized planets. The HAT-P-7 light curve in Figure 17 below compares a light curve from a ground-based transit survey for the planet HAT-P-7b with data from the Kepler space mission. What a difference the higher precision made!

In 2011, the first rocky exoplanet was discovered with the Kepler mission, known as Kepler-10 b. The lead author on the discovery paper, Natalie Batalha, was also the Deputy Scientist for the space mission, and her collaborative leadership style helped to make the NASA mission an incredible success. You can participate in the hunt for transiting planets in the Kepler data on the Zooniverse Planet Hunters website.

Multi-planet Transiting Systems

So far, we’ve only considered cases where there is just one transiting planet. In our solar system, the planets are nearly co-planar. What if there is more than one transiting planet in the time-series light-curve data? Would we be able to disentangle the different signals? If the planets are different sizes, then the transit depths will also differ. A second important parameter is the orbital period. Kepler’s third law says that the orbital period is related to the semi-major axis of the orbit so that more distant planets have longer period orbits. With longer period orbits, the time interval between transits is also longer. So there are two important pieces of information that go into a model of a transiting system: the spacing between transits (i.e., the orbital period) and the depth of the transits.

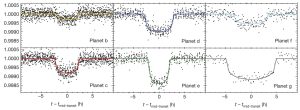
A good example of what actual data looks like for a system with more than one planet is shown in Figure 18 below for the Kepler 11 system. The six planets in this system all orbit closer than the distance to Mercury in our solar system.

After detrending the light curve to remove instrumental errors in the photometry, transits of the individual planets are phase-folded and shown below.

Astrometry

Astrometry is one of the oldest methods that astronomers have for studying the motion of stars. The name says it all: astrometry is the process of measuring the positions of objects in the sky. This technique has been used to measure parallax (distances) to stars and proper motions (motions in the plane of the sky) and to detect binary star orbits. More recently, astronomers have tried to detect exoplanets with this technique. This technique has not been very successful from ground-based telescopes because distortions from the atmosphere (“twinkling” of stars) blurs out the spatial position of stars and therefore does not permit precise enough measurements. However, astrometry as a planet detection technique is about to explode onto the scene with the launch of the space-based Gaia spacecraft in 2013 by the European Space Agency. The Gaia mission is still collecting data and, as we’ll see, it takes many, many years of data to detect exoplanets using astrometry, so any new detections with Gaia may take some time. So far, Gaia has found one exoplanet.

To date, only three exoplanets have been found using this method: DENIS-P J082303.1-491201 b, GJ 896 A b and HIP 66074 b. The first two exoplanets are gas giants that were found using ground based instruments, while the third exoplanet is the exoplanet found with Gaia.

How It Works

The basic idea behind astrometry for exoplanet detection is depicted in the animation below. Astronomers obtain a series of pictures over time (a “time series”) and use at least three reference stars (which have nearly constant positions) to measure the changing position of the host star in the plane of the sky.

Because astrometric measurements are made in two dimensions (x, y in the plane of the sky), the astrometric orbital model measures the true mass of the planet; it does not suffer from the unresolved inclination of orbital models from the radial velocity method.

It is straightforward to show that distance between the star and planet from the center-of-mass () and their masses are related by:

where

is the mass of the star

is the mass of the star

is the distance of the star from the center-of-mass

is the distance of the planet from the center-of-mass

Notice that even if you know the mass of the star (from its spectral type) and the distance between the star and the center of mass with astrometry, there are still two unknowns in the equation above: the mass of the planet and distance between the planet and the center of mass. However, astrometric observations also reveal the orbital period, so we can use Kepler’s Laws to derive the semi-major axis of the planet (the semi-major axis a is the same quantity as the distance between the planet and the center of mass). Then, if you know the mass of the star and measure the astrometric displacement of the star, you can solve for the planet mass.

Astrometry of Multi-Planet Systems

Consider our solar system. The astrometric motion of the Sun is depicted in Figure 20 below. These positional measurements assume a bird’s eye view looking down onto the orbital plane of the solar system. The larger lighter yellow circle indicates the size of the Sun, so you would need to wait long enough to see motion that is larger than this size.

The star wobble demo below will allow you to add in any planets in our solar system and see the gravitational effect on the Sun that might be observed if we were observing from above the orbital plane. However (this is an important point), to fully model an astrometric orbit, astronomers must observe the star through a large fraction of one complete orbit. This would require about 12 years of observations to detect Jupiter or 30 years for Saturn!

Gravitational Microlensing

Gravitational Lensing Basics

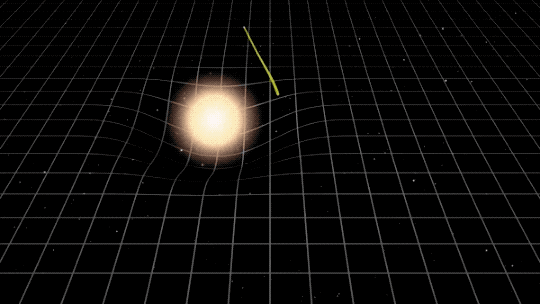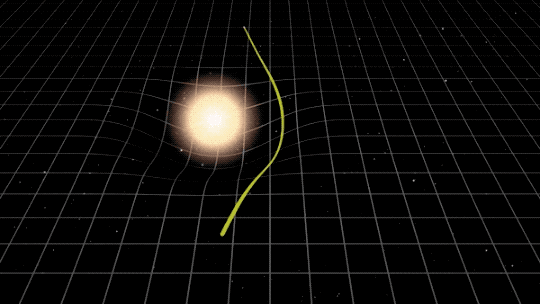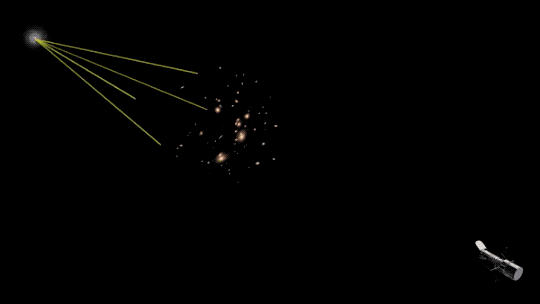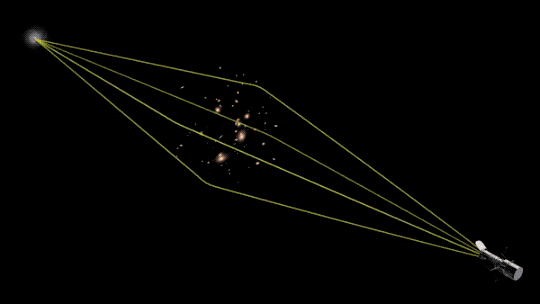
Stars emit light in all directions. When we observe a distant star we see only the few rays of light from the star that are directed straight toward us, as shown in Figure 21. However, if a foreground star passes very close to our line of sight of the more distant source star, the light from the distant background star will be gravitationally focused. To understand this idea, remember that we are the observer. The distant star is the source. The intervening star is the lens, and it bends light from the source toward us. Figure 22 below show the light path from a distant source star with an intervening “lens” star. How does the path of light from the source star differ in Figures 21 and 22?

The bending and focusing of the light from the source star in Figure 22 is caused by the gravity of the lens star. To fully understand why light is bent, gravity needs to be considered as described by Albert Einstein. In 1915, Einstein published his General Theory of Relativity, treating gravity as a warping of the space-time continuum and an attribute of mass rather than a fundamental force. Einstein’s description of gravity employs mathematically sophisticated metric tensors, while Newtonian gravity uses more commonly accessible algebra or calculus. On the scales that humans are accustomed to working with, general relativity converges to the Newtonian description, so we are justified in defaulting to the Newtonian description of gravity. More details are given in the box below.

Want to know more: General Relativity and Space-Time

Sir Isaac Newton considered space and time to be completely independent, and that continued to be the accepted view until the beginning of the twentieth century. But Albert Einstein showed that there is an intimate connection between space and time, and that only by considering the two together—in what we call spacetime—can we build up a correct picture of the physical world. We examine spacetime a bit more closely in the next subsection.

The gist of Einstein’s Theory of General Relativity is that the presence of matter curves or warps the fabric of spacetime. This curving of spacetime is identified with gravity. When something else—a beam of light, an electron, or the starship Enterprise—enters such a region of distorted spacetime, its path will be different from what it would have been in the absence of the matter. As American physicist John Wheeler summarized it: “Matter tells spacetime how to curve; spacetime tells matter how to move.”

Spacetime is four-dimensional: three space dimensions and one time dimension (the time dimension is also warped but will do not discuss that further here). The warping of the space dimensions is sometimes shown as a 2-D grid, as in the part of the animation below that shows light bent around a single star. The light is following the shortest path it can take as it encounters the warped space.

The amount of distortion in spacetime depends on the mass of material that is involved and on how concentrated and compact it is. Terrestrial objects, such as people and buildings, have far too little mass to introduce any significant distortion.

Every object with mass has a gravitational field. We can think of objects with spherical symmetry, like stars or planets, as point sources. The strength of the gravitational field for a star is spherically symmetric. The strength of the gravitational field for a star is spherically symmetric. When we consider gravitational lensing, the relevant geometry is a slice through the sphere – a disk perpendicular to our line of sight.

Qualitatively, the gravitational field at small radii on this disk (i.e., closest to the lensing object) is strongest, and light from the source is bent so strongly that it converges closer to the lensing object and does not reach the observer. Likewise, the gravitational field is weakest at large radii on the disk, and light from the source star focuses at distances beyond the observer. However, there is a ring on the disk where the bending of light from the source is “just right.” Those rays of light from the source are brought to a focus at the position of the observer. This effect is called gravitational lensing, and it was predicted in 1936 by Einstein. The ring of light that is focused at the position of the observer is given the special name of an Einstein ring.

The size of the Einstein ring depends on the mass of the lens star, the distance between the observer and the lens, D_L, and the distance from the observer to the source, D_S. Gravitational lensing occurs even if the lens star is too faint for us to see. Since most of the stars in galaxy are low mass, low luminosity M dwarf stars, this is often the case!

Since lensing is an effect of gravity, it might seem like the amplitude of brightening will depend on the mass of the lens.  While the mass of the lensing star determines the radius of the Einstein ring and the duration of the lensing event, the amplitude of brightening is most sensitive to something called the impact parameter.  When the lensing object precisely lines up with our view to the source star, the impact parameter is zero and the magnification in brightness is a maximum.  If the lensing object is not as tightly aligned with our view of the source – perhaps it just clips our view of the source star, then the impact parameter is larger and the brightening of the source star (the “magnification”) is not as strong. This is depicted in Figure 23 below. The Einstein ring is represented by the dashed circle. The red, yellow, green, and blue lines show the path that the lensing object travels with different offsets from precise alignment with our view of the source. The closer the alignment of the Einstein ring of the lens to our view of the source, the stronger the magnification that we observe. Gravitational lensing from objects as massive as stars typically lasts for several days.

Microlensing

Gravitational lensing generally refers to the bending of light from a background source by a foreground massive object. Gravitational microlensing is a special case where multiple lensing events occur from more than one foreground mass. If the lensing star happens to have orbiting planets that also cross our line of sight to the source star, then a second microlensing event is superimposed during the brightening event. Because the mass of the orbiting planet is smaller than the mass of a star, the duration of the second microlensing event will be shorter, but since the alignment of the lensing planet is essentially the same as the alignment of the host star, the amplitude of the magnification will be similar.

The video below summarizes how microlensing searches are carried out at observatories today this clip highlights the Las Cumbres Observatory Global Telescope Network).

Detecting exoplanets with microlensing.

 

 

Video source: Las Cumbres Observatory CC BY-NC 2.0

Review Questions

Summary Questions

1. How is the transit method used to detect exoplanets? Describe what a light curve is.
2. How does the dip in brightness caused by a transiting planet vary with the size (radius) of the planet? What if there are multiple planets transiting a star at the same time?
3. Why don’t each of the eight planets in our solar system induce identical astrometric movements of the Sun? Which planet causes the largest “wobble” of the Sun? Why?
4. What is gravitational lensing and microlensing?
5. How can gravitational microlensing be used to detect exoplanets?

Exercises

1. Consider the three methods for detecting exoplanets discussed in this chapter and make a chart listing the advantages of each method and what type of exoplanet it is best at finding.
2. Transit simulator activities