9 Factor Analysis Overview
You can load this file with open_template_file(“factoranalysis”).
Background: https://usq.pressbooks.pub/statisticsforresearchstudents/part/factor-analysis/ https://advstats.psychstat.org/book/factor/efa.php for an overview, though there are many introductions that cover the same general territory.
Sage: Kim, J., & Mueller, C. W. (1978). Factor analysis. SAGE Publications, Inc., https://doi.org/10.4135/9781412984256
Finch, W. (2020). Exploratory factor analysis. SAGE Publications, Inc., https://doi.org/10.4135/9781544339900
We have seen that the scales in the ethics1 data set are at list minimally internally reliable, but the weakest ones are DS_OD and DS_ID.
ggplot(data = ethics1, aes(x= DS_OD, y= DS_ID)) +geom_jitter() +geom_smooth(method = "lm", se = FALSE)
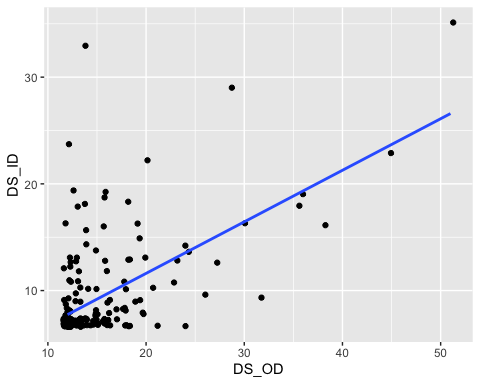
Clearly they are positively associated, but there are some high values
for both scales that are possibly very influential and making
the line seem steeper than it might be if they weren’t there.
Remember that DS_ID was constructed from 7 items and DS_OD used 12 items. If you look at the ethics vignette you can see the specific items.
Looking at the correlation matrix for the original 19 variables we can see that these vary quite a bit.
# This creates a data frame with just our variables of interest.ethics1[complete.cases(ethics1) == TRUE,] |>select(starts_with("DS_ID_") | starts_with("DS_OD_")) |> haven::zap_labels() -> DS_data# This creates a correlation matrix for those variables. DS_data |> cor() -> DS_cor# Rounding will make it easier to read.round(DS_cor, 2)
## DS_ID_1 DS_ID_2 DS_ID_3 DS_ID_4 DS_ID_5 DS_ID_6 DS_ID_7 DS_OD_1## DS_ID_1 1.00 0.47 0.43 0.49 0.42 0.46 0.28 0.22## DS_ID_2 0.47 1.00 0.57 0.46 0.51 0.62 0.44 0.31## DS_ID_3 0.43 0.57 1.00 0.43 0.33 0.46 0.20 0.34## DS_ID_4 0.49 0.46 0.43 1.00 0.47 0.38 0.17 0.24## DS_ID_5 0.42 0.51 0.33 0.47 1.00 0.20 0.52 0.16## DS_ID_6 0.46 0.62 0.46 0.38 0.20 1.00 0.43 0.35## DS_ID_7 0.28 0.44 0.20 0.17 0.52 0.43 1.00 0.28## DS_OD_1 0.22 0.31 0.34 0.24 0.16 0.35 0.28 1.00## DS_OD_2 0.33 0.32 0.23 0.22 0.20 0.21 0.23 0.27## DS_OD_3 0.06 0.14 0.43 0.06 0.06 0.15 0.13 0.39## DS_OD_4 0.43 0.36 0.30 0.28 0.23 0.42 0.25 0.46## DS_OD_5 0.31 0.22 0.27 0.24 0.16 0.29 0.25 0.28## DS_OD_6 0.30 0.37 0.30 0.28 0.35 0.30 0.38 0.32## DS_OD_7 0.34 0.57 0.45 0.32 0.24 0.50 0.31 0.29## DS_OD_8 0.38 0.43 0.26 0.18 0.16 0.38 0.34 0.40## DS_OD_9 0.35 0.43 0.42 0.29 0.15 0.51 0.31 0.55## DS_OD_10 0.13 0.10 0.13 0.08 0.09 0.10 0.14 0.50## DS_OD_11 0.36 0.47 0.25 0.18 0.20 0.37 0.29 0.39## DS_OD_12 0.28 0.36 0.37 0.34 0.26 0.38 0.37 0.67## DS_OD_2 DS_OD_3 DS_OD_4 DS_OD_5 DS_OD_6 DS_OD_7 DS_OD_8 DS_OD_9## DS_ID_1 0.33 0.06 0.43 0.31 0.30 0.34 0.38 0.35## DS_ID_2 0.32 0.14 0.36 0.22 0.37 0.57 0.43 0.43## DS_ID_3 0.23 0.43 0.30 0.27 0.30 0.45 0.26 0.42## DS_ID_4 0.22 0.06 0.28 0.24 0.28 0.32 0.18 0.29## DS_ID_5 0.20 0.06 0.23 0.16 0.35 0.24 0.16 0.15## DS_ID_6 0.21 0.15 0.42 0.29 0.30 0.50 0.38 0.51## DS_ID_7 0.23 0.13 0.25 0.25 0.38 0.31 0.34 0.31## DS_OD_1 0.27 0.39 0.46 0.28 0.32 0.29 0.40 0.55## DS_OD_2 1.00 0.16 0.60 0.40 0.41 0.38 0.58 0.31## DS_OD_3 0.16 1.00 0.08 0.22 0.34 0.37 0.22 0.19## DS_OD_4 0.60 0.08 1.00 0.46 0.38 0.34 0.60 0.51## DS_OD_5 0.40 0.22 0.46 1.00 0.41 0.40 0.41 0.42## DS_OD_6 0.41 0.34 0.38 0.41 1.00 0.57 0.54 0.48## DS_OD_7 0.38 0.37 0.34 0.40 0.57 1.00 0.52 0.52## DS_OD_8 0.58 0.22 0.60 0.41 0.54 0.52 1.00 0.42## DS_OD_9 0.31 0.19 0.51 0.42 0.48 0.52 0.42 1.00## DS_OD_10 0.19 0.25 0.22 0.28 0.11 0.10 0.29 0.43## DS_OD_11 0.48 0.12 0.46 0.43 0.53 0.50 0.62 0.46## DS_OD_12 0.38 0.29 0.38 0.38 0.44 0.41 0.39 0.67## DS_OD_10 DS_OD_11 DS_OD_12## DS_ID_1 0.13 0.36 0.28## DS_ID_2 0.10 0.47 0.36## DS_ID_3 0.13 0.25 0.37## DS_ID_4 0.08 0.18 0.34## DS_ID_5 0.09 0.20 0.26## DS_ID_6 0.10 0.37 0.38## DS_ID_7 0.14 0.29 0.37## DS_OD_1 0.50 0.39 0.67## DS_OD_2 0.19 0.48 0.38## DS_OD_3 0.25 0.12 0.29## DS_OD_4 0.22 0.46 0.38## DS_OD_5 0.28 0.43 0.38## DS_OD_6 0.11 0.53 0.44## DS_OD_7 0.10 0.50 0.41## DS_OD_8 0.29 0.62 0.39## DS_OD_9 0.43 0.46 0.67## DS_OD_10 1.00 0.38 0.60## DS_OD_11 0.38 1.00 0.46## DS_OD_12 0.60 0.46 1.00
A visualization can be helpful for seeing patterns.
#notice that the figure size is adjusted.corrplot::corrplot(DS_cor, method = 'color')
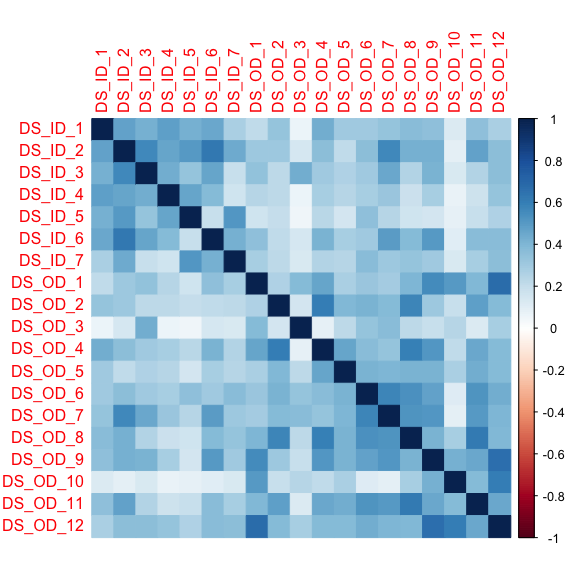
corrplot::corrplot(DS_cor, order = 'AOE')
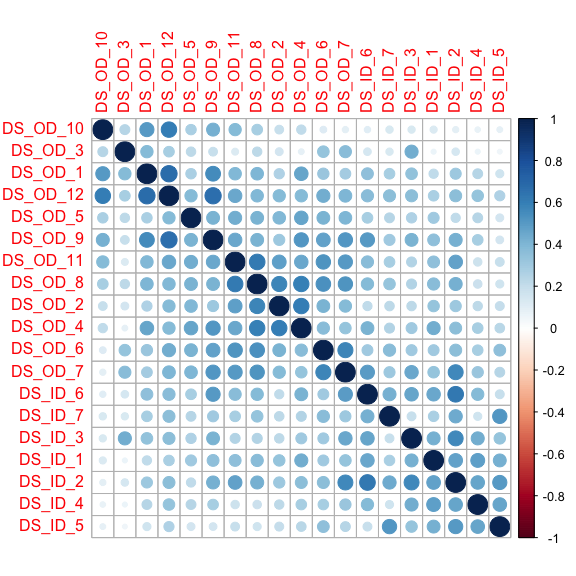
corrplot::corrplot(DS_cor, order = ‘hclust’, addrect = 5)
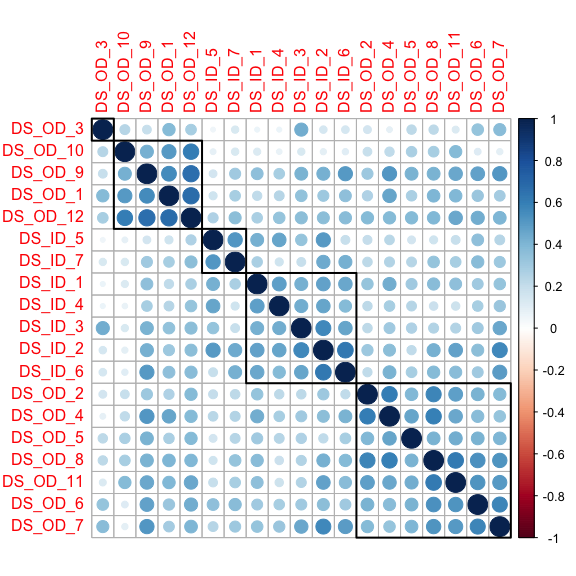
There are many other options for displaying the correlation matrix, which you can see here: https://cran.r-project.org/web/packages/corrplot/vignettes/corrplot-intro.html
How many factors are there?
ev <- eigen(DS_cor) # get eigenvaluesev$values
## [1] 7.3216335 1.8875037 1.4382953 1.1918764 1.0513941 0.9402367 0.7320710## [8] 0.6899644 0.6261405 0.5065023 0.4623007 0.4337202 0.3475235 0.3164977## [15] 0.2865786 0.2289359 0.2207224 0.1679963 0.1501070
psych::scree(DS_data)
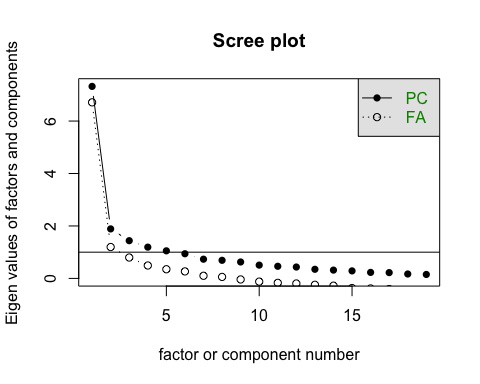
psych::fa.parallel(DS_data, fa = "fa")
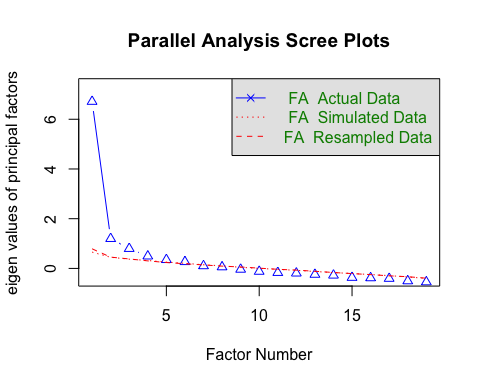
## Parallel analysis suggests that the number of factors = 6 and the number of components = NA
In this case it seems like there are actually 5 factors, not two.
DS_data |> factanal( factors = 6, scores = "Bartlett") -> fa5fa5
## ## Call:## factanal(x = DS_data, factors = 6, scores = "Bartlett")## ## Uniquenesses:## DS_ID_1 DS_ID_2 DS_ID_3 DS_ID_4 DS_ID_5 DS_ID_6 DS_ID_7 DS_OD_1 ## 0.591 0.288 0.430 0.609 0.005 0.371 0.624 0.379 ## DS_OD_2 DS_OD_3 DS_OD_4 DS_OD_5 DS_OD_6 DS_OD_7 DS_OD_8 DS_OD_9 ## 0.497 0.005 0.005 0.659 0.439 0.346 0.337 0.346 ## DS_OD_10 DS_OD_11 DS_OD_12 ## 0.469 0.392 0.173 ## ## Loadings:## Factor1 Factor2 Factor3 Factor4 Factor5 Factor6## DS_ID_1 0.248 0.459 0.301 0.202 ## DS_ID_2 0.320 0.695 0.350 ## DS_ID_3 0.610 0.156 0.186 0.349 ## DS_ID_4 0.474 0.135 0.367 ## DS_ID_5 0.202 0.970 ## DS_ID_6 0.241 0.730 0.151 0.118 ## DS_ID_7 0.271 0.256 0.177 0.452 ## DS_OD_1 0.187 0.226 0.659 0.213 0.228 ## DS_OD_2 0.587 0.155 0.113 0.338 ## DS_OD_3 0.153 0.207 0.959 ## DS_OD_4 0.445 0.246 0.210 0.826 ## DS_OD_5 0.449 0.155 0.244 0.204 ## DS_OD_6 0.622 0.186 0.181 0.258 0.199 ## DS_OD_7 0.576 0.496 0.102 0.224 ## DS_OD_8 0.735 0.195 0.171 0.225 ## DS_OD_9 0.337 0.448 0.559 0.163 ## DS_OD_10 0.152 0.702 ## DS_OD_11 0.684 0.222 0.279 ## DS_OD_12 0.278 0.256 0.809 0.161 ## ## Factor1 Factor2 Factor3 Factor4 Factor5 Factor6## SS loadings 3.057 2.717 2.321 1.673 1.212 1.054## Proportion Var 0.161 0.143 0.122 0.088 0.064 0.055## Cumulative Var 0.161 0.304 0.426 0.514 0.578 0.633## ## Test of the hypothesis that 6 factors are sufficient.## The chi square statistic is 230.2 on 72 degrees of freedom.## The p-value is 1.96e-18
For contrast, we can also see what the 2-factor solution looks like.
DS_data |>factanal( factors = 2) -> fa2fa2
## ## Call:## factanal(x = DS_data, factors = 2)## ## Uniquenesses:## DS_ID_1 DS_ID_2 DS_ID_3 DS_ID_4 DS_ID_5 DS_ID_6 DS_ID_7 DS_OD_1 ## 0.605 0.342 0.616 0.695 0.715 0.521 0.728 0.436 ## DS_OD_2 DS_OD_3 DS_OD_4 DS_OD_5 DS_OD_6 DS_OD_7 DS_OD_8 DS_OD_9 ## 0.702 0.862 0.597 0.709 0.599 0.494 0.559 0.408 ## DS_OD_10 DS_OD_11 DS_OD_12 ## 0.474 0.551 0.289 ## ## Loadings:## Factor1 Factor2## DS_ID_1 0.607 0.161 ## DS_ID_2 0.795 0.161 ## DS_ID_3 0.574 0.233 ## DS_ID_4 0.536 0.133 ## DS_ID_5 0.531 ## DS_ID_6 0.648 0.244 ## DS_ID_7 0.465 0.235 ## DS_OD_1 0.207 0.722 ## DS_OD_2 0.402 0.370 ## DS_OD_3 0.154 0.338 ## DS_OD_4 0.459 0.439 ## DS_OD_5 0.337 0.421 ## DS_OD_6 0.504 0.383 ## DS_OD_7 0.641 0.309 ## DS_OD_8 0.491 0.447 ## DS_OD_9 0.408 0.652 ## DS_OD_10 0.722 ## DS_OD_11 0.458 0.489 ## DS_OD_12 0.272 0.798 ## ## Factor1 Factor2## SS loadings 4.450 3.649## Proportion Var 0.234 0.192## Cumulative Var 0.234 0.426## ## Test of the hypothesis that 2 factors are sufficient.## The chi square statistic is 721.19 on 134 degrees of freedom.## The p-value is 3.24e-81
We use rotations to simplify the representation of the factors.
There are many options, let’s use promax as an example.
DS_data |> factanal( factors = 5, scores = "Bartlett", rotation = "promax") -> fa5pprint(fa5p, cut=0.2)
## ## Call:## factanal(x = DS_data, factors = 5, scores = "Bartlett", rotation = "promax")## ## Uniquenesses:## DS_ID_1 DS_ID_2 DS_ID_3 DS_ID_4 DS_ID_5 DS_ID_6 DS_ID_7 DS_OD_1 ## 0.557 0.314 0.553 0.621 0.005 0.330 0.633 0.409 ## DS_OD_2 DS_OD_3 DS_OD_4 DS_OD_5 DS_OD_6 DS_OD_7 DS_OD_8 DS_OD_9 ## 0.461 0.750 0.248 0.654 0.403 0.272 0.338 0.364 ## DS_OD_10 DS_OD_11 DS_OD_12 ## 0.464 0.473 0.193 ## ## Loadings:## Factor1 Factor2 Factor3 Factor4 Factor5## DS_ID_1 0.294 0.431 ## DS_ID_2 0.655 0.216 ## DS_ID_3 0.578 ## DS_ID_4 0.421 0.281 ## DS_ID_5 1.074 ## DS_ID_6 0.895 -0.247 ## DS_ID_7 0.412 ## DS_OD_1 0.729 ## DS_OD_2 0.764 ## DS_OD_3 0.240 0.452 ## DS_OD_4 0.895 -0.290 ## DS_OD_5 0.411 ## DS_OD_6 0.250 0.590 ## DS_OD_7 0.356 0.736 ## DS_OD_8 0.701 0.280 ## DS_OD_9 0.499 0.349 ## DS_OD_10 0.862 -0.244 ## DS_OD_11 0.443 0.307 ## DS_OD_12 0.871 ## ## Factor1 Factor2 Factor3 Factor4 Factor5## SS loadings 2.478 2.441 2.330 1.628 1.544## Proportion Var 0.130 0.128 0.123 0.086 0.081## Cumulative Var 0.130 0.259 0.382 0.467 0.548## ## Factor Correlations:## Factor1 Factor2 Factor3 Factor4 Factor5## Factor1 1.000 0.367 -0.271 -0.568 -0.346## Factor2 0.367 1.000 -0.571 -0.543 -0.559## Factor3 -0.271 -0.571 1.000 0.476 0.543## Factor4 -0.568 -0.543 0.476 1.000 0.470## Factor5 -0.346 -0.559 0.543 0.470 1.000## ## Test of the hypothesisthat 5 factors are sufficient.
## The chi square statistic is 323.4 on 86 degrees of freedom.## The p-value is 3.33e-29
One of the interesting things to notice is that DS_OD_3 is not by itself the way it was when we looked at the bivariate correlation matrix. This is also true for some of the other rectangles that were highlighted. This is because factor analysis is a multivariate method, controlling for many variables at once. When you do that the bivariate relationships can change.
One of the decisions about rotations is whether the factors should be allowed to be correlated or must be uncorrelated (orthogonal) with each other. The promax rotation allows them to be correlated. To see the implications of this we can compare the correlations of the factors created in fa5 and fa5p.
round(cor(fa5$scores), 2)
## Factor1 Factor2 Factor3 Factor4 Factor5 Factor6## Factor1 1.00 -0.11 -0.07 0.01 -0.02 -0.09## Factor2 -0.11 1.00 -0.04 -0.04 0.00 0.01## Factor3 -0.07 -0.04 1.00 0.01 -0.02 0.00## Factor4 0.01 -0.04 0.01 1.00 0.00 0.00## Factor5 -0.02 0.00 -0.02 0.00 1.00 0.02## Factor6 -0.09 0.01 0.00 0.00 0.02 1.00
round(cor(fa5p$scores), 2)
## Factor1 Factor2 Factor3 Factor4 Factor5## Factor1 1.00 0.50 0.46 0.35 0.46## Factor2 0.50 1.00 0.41 0.25 0.47## Factor3 0.46 0.41 1.00 0.54 0.34## Factor4 0.35 0.25 0.54 1.00 0.31## Factor5 0.46 0.47 0.34 0.31 1.00
From a criminology perspective we would probably expect that deviance of different types would be correlated, so it is likely we would use the rotated scores.
We can use these scores for further analysis or we could use summary scales with Cronbach’s α the way we did previously.