Sec. 3.1 – Venn Diagrams, Complement, Intersection and Union
Chapter 3, Section 1
Math Topics – Venn Diagrams, Complement, Intersection and Union
Elementary Education – Sorting and Organizing
Sets
Sets can be used to sort and organize objects and ideas. In this section, you’ll see sets used to describe shapes, numbers, and even children in a classroom.
For a fun icebreaker for this section, try: https://www.setgame.com/set/puzzle. This is a fun sorting game where third graders tend to beat grownups! Try it out yourself. Read the rules first, and look at the previous day’s solutions. Warning: my kid was (and still is) better than me at this! But with the whole class playing together, you can do it!
Some beginning vocabulary:
- A set is a collection of objects.
- The objects in a set are called the elements of that set.
- We can describe a set in words, or we can list the elements inside curly braces { }.
- Venn diagrams are a way to visualize the elements in sets, by putting a circle around all elements in the same set.
- The universal set is all objects currently under consideration. We put a box around all the items in the universal set.
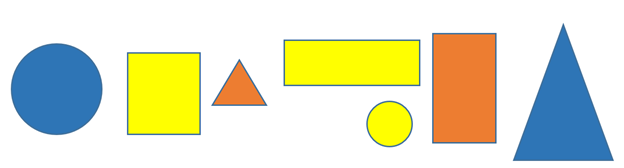
Example 1 Just as children collect different blocks or buttons together to make sets, let’s make our own set from the shapes in the chapter introduction. What is one set you can think of making using common characteristics of some of these shapes? Describe your set idea using words, and then list the elements inside curly braces, then show the elements of your set in a circle, with the other elements outside. There are many possibilities!
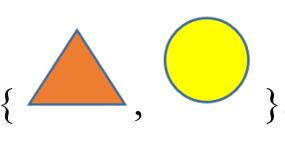
In words, one possible set is all the small shapes. In a list, this would be:
Notice that we write the two elements inside curly braces to show they are a set.
Using a Venn diagram, we would show those two elements inside a circle, with all the other elements outside it. We place a box around all the objects, to show that this is our universal set — all the shapes from the chapter intro.
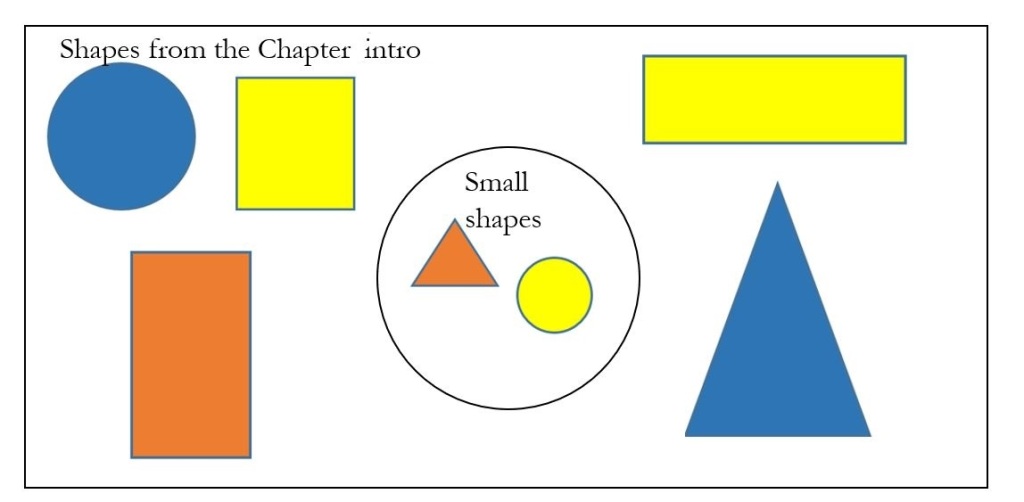
You can probably think of a different set than this one! In the homework, you will share your idea, along with your list and Venn diagram.
Example 2 Suppose we have the integers from 1 to 10. There are many ways we can make sets from those numbers. One set we could make is the multiples of 2. Reminder: the multiples of a number are gotten by multiplying that number by each of the integers. Some multiples of 2 are 2 × 1, 2 × 2, 2 × 3, 2 × 4, etc. How can we show this in list form and in a Venn Diagram? What is our universal set?
In a list, the multiples of 2 between 1 and 10 are: {2, 4, 6, 8, 10}.
In a Venn Diagram, we would have a circle with multiples of 2 inside it, and everything else outside:
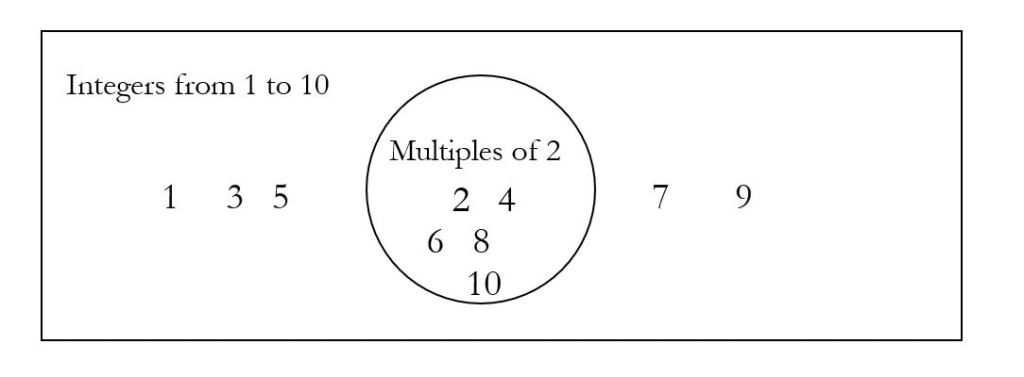
Our universal set is all the numbers from 1 to 10: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Question: Now you try! How would you write the multiples of three between 1 and 10 using first a list and then a Venn diagram? Try it, then check your answer, here.
You might have noticed in examples 1 and 2, we didn’t talk about all the shapes in the world, or all the integers. In example 1, we just talked about the shapes in the chapter 1 intro. In example 2, we just talked about the numbers from 1 to 10. Limiting our set in this way helps us to study it and to see what is in it, and what is not in it, more easily. But sometimes we will also talk about all the integers, or all of some other category, like shapes or animals. That means it’s important to state what our universal set is, what the objects are that we are studying.
Example 3 Guess my Rule! Using the picture below, what is the universal set, U, and what rule describes set A?
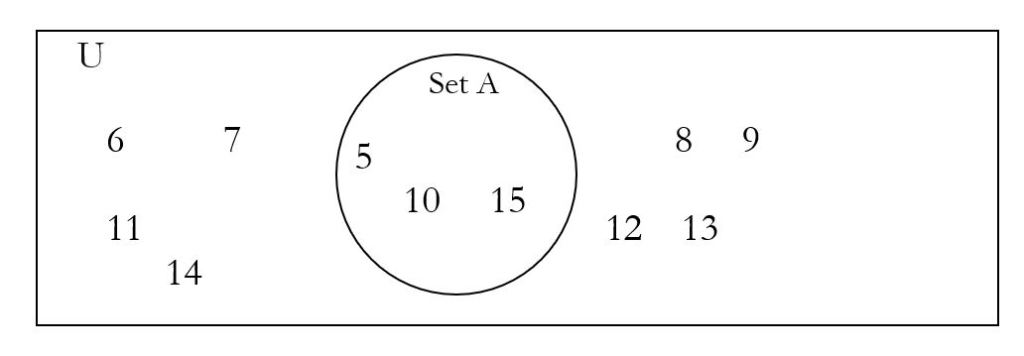
The universal set is the numbers from 5 to 15: {5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}. Set A is the multiples of 5 between 5 and 15: {5, 10, 15}.
Note that the universal set is not the objects outside the circle, but instead, it’s all the objects inside the rectangle – all the objects under consideration.
The Empty Set
Sometimes, a set might have no elements in it. In that case, this set is called the empty set, and it is written as curly braces with noting inside it, { }, or using the symbol ∅. Note that we do not write {∅}, because that’s not an empty set — that’s a set that has a symbol in it!
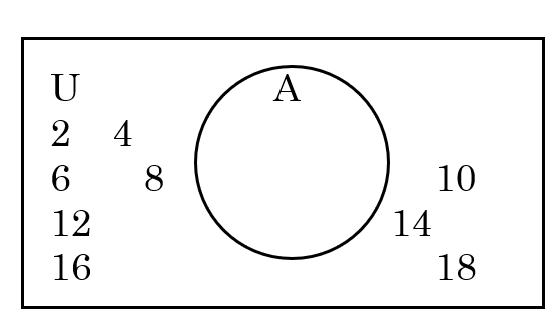
Example 4 Suppose the Universal set, U, is the multiples of 2 from 2 to 18, and set A is the multiples of 11 in U. How would you write each set in a list, and how would you draw the Venn Diagram?
In a list, you would write U = {2, 4, 6, 8, 10, 12, 14, 16, 18} and A = { } (or A = ∅)
Complement
The complement of set A is written A|. It means, all the elements not in A, but still in the universal set. The symbol after the A is a straight quote mark (the straightened version of ‘).
Example 5 Using our previous example 3, with A = multiples of 5 between 5 and 15 = {5, 10, 15}, this would mean that A| is all the numbers from 5 to 15 that are not multiples of 5. These are numbers outside of A, but still in the universal set, shown below, shaded in yellow.
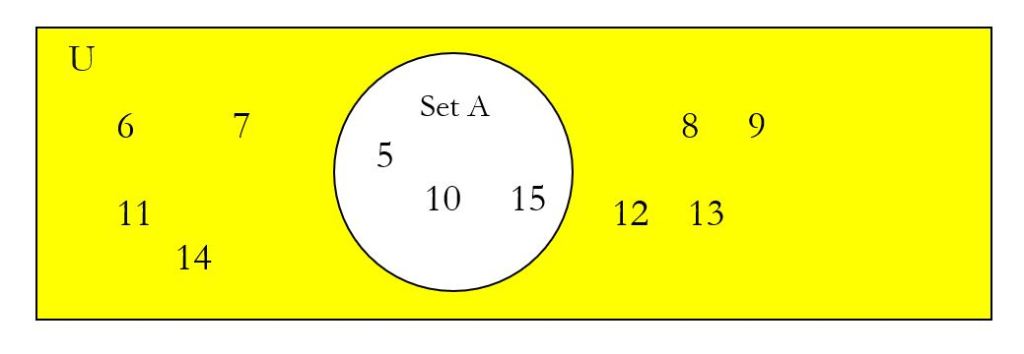
Thus, A| = {6, 7, 8, 9, 11, 12, 13, 14}
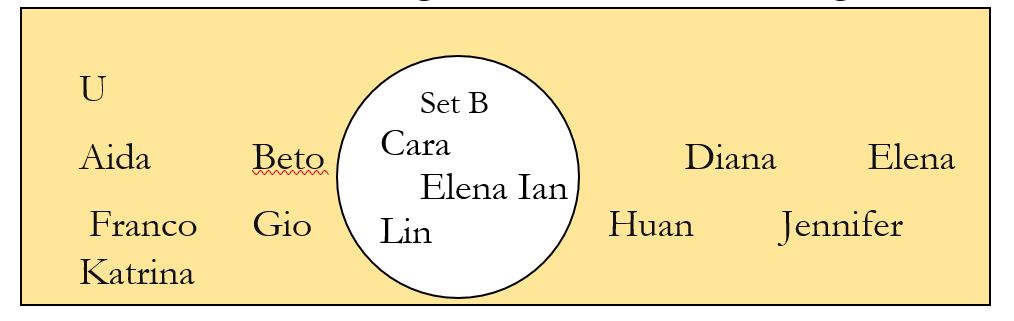
Example 6 Suppose the universal set is all the students in a classroom, and set B is the students in the class who are wearing blue shoes. How would you describe the complement of B, in words?
Imagine that U = {Aida, Beto, Cara, Diana, Elena, Franco, Gio, Huan, Ian, Jennifer, Katrina, Lin} and B = {Cara, Elena, Ian, Lin}. Describe B| in words, in a list, and using a Venn Diagram. B| is the area in the Venn diagram that is shaded in orange.
Combining Two Sets: Intersection, Union and Complement
In the previous example, suppose some of the students in the class like apples. We can call these students, set A.
A = students who like apples = {Beto, Cara, Diana, Ian, Jennifer}.
Recall that B = {Cara, Elena, Ian, Lin} and notice that sets A and B have some of the same students. When we draw the diagram, we put each student in only one place in the diagram.
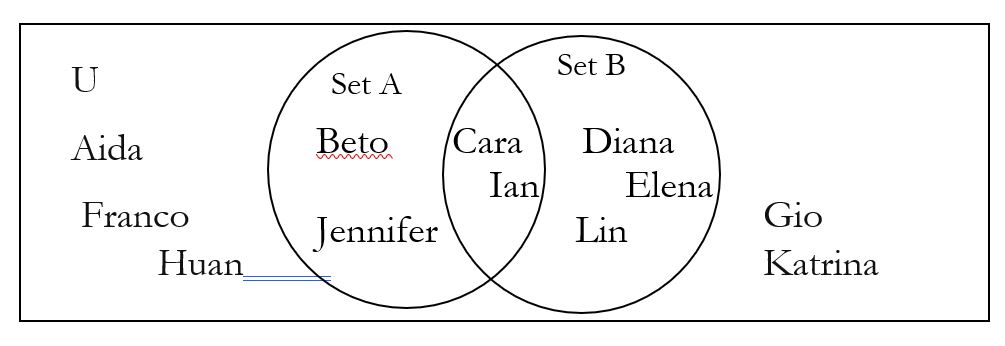
In words, A ∩ B = students who like apples and have blue shoes. In list form, A ∩ B = {Cara, Ian}.
Suppose we want to talk about all the students in both sets. In that case, we use the union of the two sets, A ∪ B.
In list form, A ∪ B = {Beto, Cara, Diana, Elena, Ian, Jennifer, Lin}. In words, A ∪ B = students who like apples or have blue shoes.
Quick Key
| Intersection | Union | Empty Set | Complement | |
| Meaning | The overlap of the two sets | All of the two sets | A set with nothing in it. | The area outside of A. |
| Symbol | A ∩ B | A ∪ B | ∅ | A’ |
| Words | A and B | A or B | empty | not A |
| Picture | 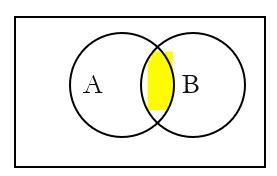 |
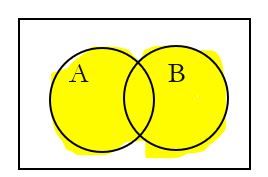 |
a set with nothing in it | 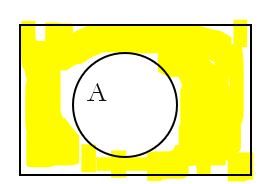 |
| To help you remember | The words intersection, and Both have n as the second letter. The ∩ looks like an n. | The word union starts with the letter U, which looks like the symbol, ∪. | The symbol ∅ looks like a zero, and the set has zero elements in it. | Think always of the word “not,” instead of the fancy word complement! 😊 |
Classroom Activity
In our college math classroom, can we think of two interesting characteristics that might describe some of us? Then we can think of where each of us is in the Venn diagrams we create. Are you in the intersection? Are you outside both circles? How can you describe yourself using the sets we make? Is there an empty set inside our set? (That would be a set that no one goes into.) Caution: as with the children in our future classrooms, we should think of characteristics that are fun and interesting, but that won’t divide or stereotype us.
Example 7 Suppose the universal set is the numbers from 5 to 15, A = the multiples of 5, and B = the multiples of 2. Draw the Venn diagram of these sets, remembering to put each element in only one place. Next, find each of these on the Venn Diagram. Write it in words and in a list.
b. A ∩ B
c. A ∪ B
d. A|
e. B|
[Don’t scroll down until you have tried each one!]
Venn Diagram
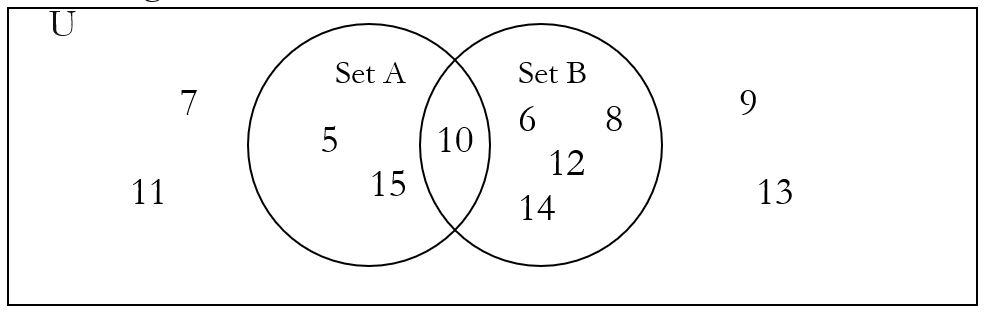
Notice that we only write the number 10 once. We put the number 10 in the middle between sets A and B, because it is in both set A (multiple of 5) and set B (multiple of 2).
a. A ∩ B = the number that is in both set A and B, in the overlap, or intersection.
In words, A ∩ B = numbers that are multiples of 5 and multiples of 2. In a list, A ∩ B = {10}
b. A ∪ B is all of both sets, the union.
In words, A ∪ B = numbers that are a multiple of 5 or a multiple of 2. In a list A ∪ B = {5, 15, 10, 6, 12, 8, 14}, or if you like to write the numbers in order, A ∪ B = {5, 6, 8, 10, 12, 14, 15} (note that these are both the same set, no matter what order you choose to write the elements).
c. A| is shaded in yellow, below. It is all the numbers outside of A, but still in the universal set.
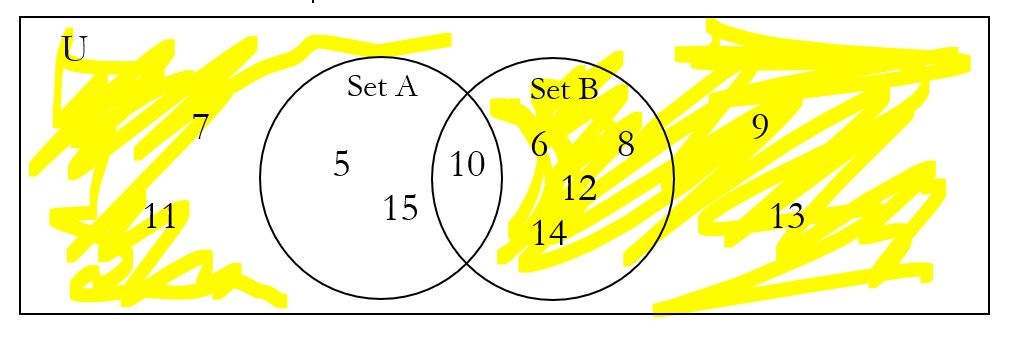
In words, A| = the numbers from 5 to 15 that are not multiples of 5 = {6, 7, 8, 9, 11, 12, 13, 14} just as it was in example 3.
Even though we have added set B to our Venn diagram, A| is still all the numbers that are outside of A, even some that are in B. Notice that when we translate into words, we don’t need to mention set B.
d. B| is shaded in green, below. It is all the numbers outside of B, but still in the universal set.
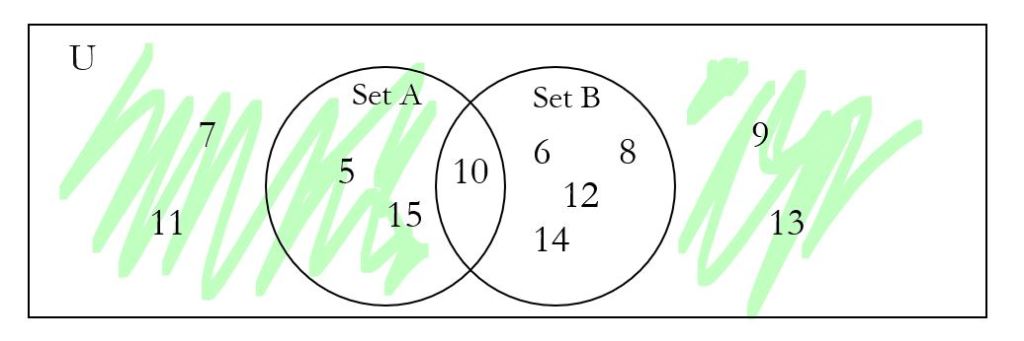
B| = the numbers from 5 to 15 that are not multiples of 2 = {5, 7, 9, 11, 13, 15}
Notice that we don’t worry if some of B| is in A.
B| is everything outside of B.
Combining Intersection and Union with Complement
What happens when we combine our three symbols, intersection, union and complement? For example, how can we find (A U B)| or A| ∩ B? Just as in our previous examples, there are three useful strategies, very similar to the problem solving strategies we talked about in chapter 2.
- Describe the sets in words.
- Shade the Venn diagram.
- List the elements.
Let’s first try using the words that describe the set, remembering that U is or, ∩ is and, | is not.
Example 7 Using the students in example 6, with A = students who like apples, B = students wearing blue shoes, find (A ∪ B)| in words and on the Venn Diagram.
To describe (A U B)| in words, first think of how to describe A U B. These are students who like apples or are wearing blue shoes.
Next, we note that the ( ) group those students together, so the | is for that whole group. We write: the students who do not like apples or wear blue shoes.
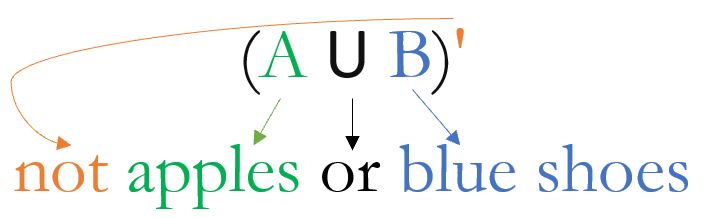
We only write the word “not” once, since there is only one complement symbol. We write “not” in front, to show that it applies to the whole group of students that is in (A ∪ B).
If we look at the Venn diagram, we can first shade all of set A with set B, remembering that for U, we shade all. This is A ∪ B.
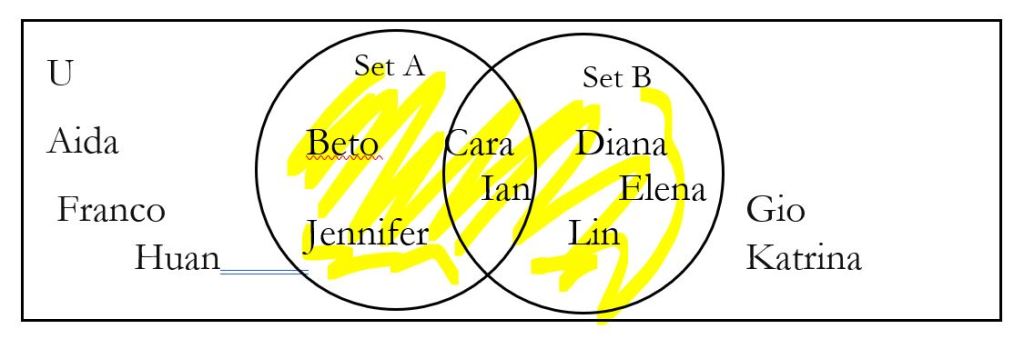
Next, we shade what is outside A ∪ B using a new color. This is (A ∪ B)|.
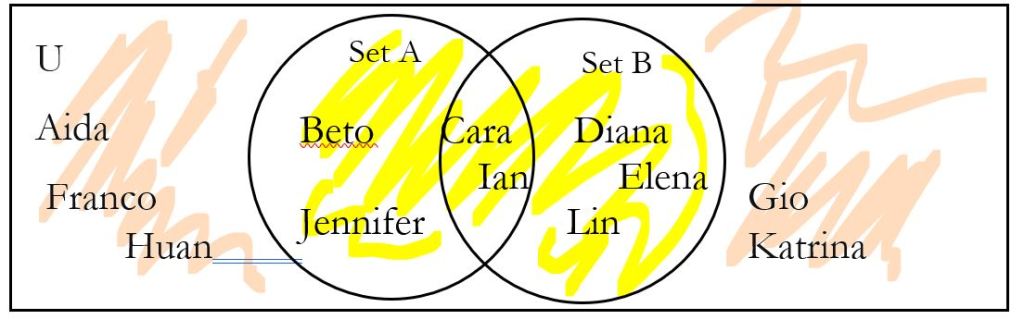
Thus, shaded in orange, (A ∪ B)| = the students who do not like apples or wear blue shoes = {Aida, Franco, Huan, Gio, Katrina}
We have used words and a diagram to find these answers. We will discuss the third method, listing the elements, more in the next section. For now, let’s look at one more example.
Example 8 Again using the same set of students, find A| ∩ B in words and in list form.
We can again use our students to describe A| ∩ B in words. A = students who like apples, so A| = students who do not like apples. The ∩ symbol always translates as the word and. Thus, these are the students who do not like apples and are wearing blue shoes.
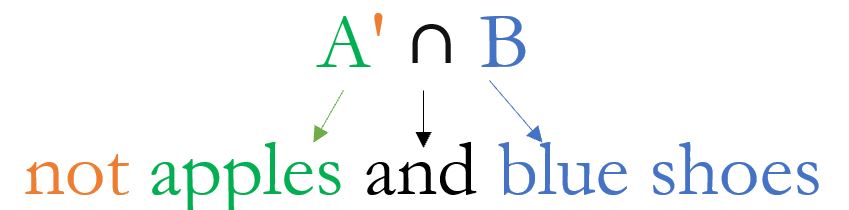
If we look at the Venn diagram, we can first shade what is not in set A, remembering that for |, we shade the outside. This is A|.
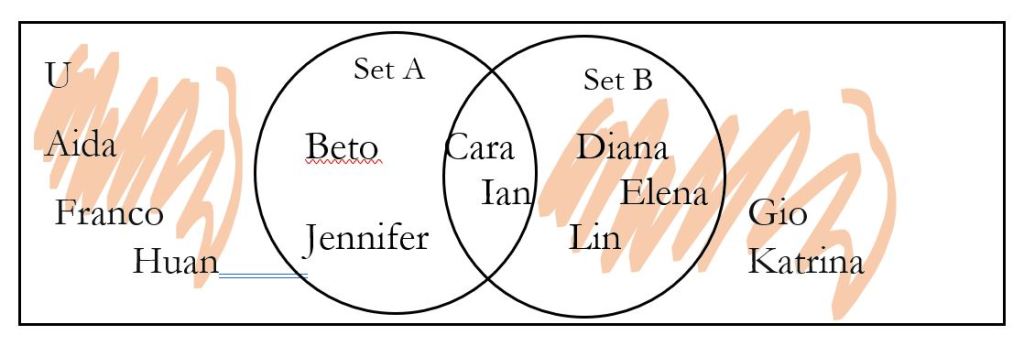
Next, we shade set B in a new color.
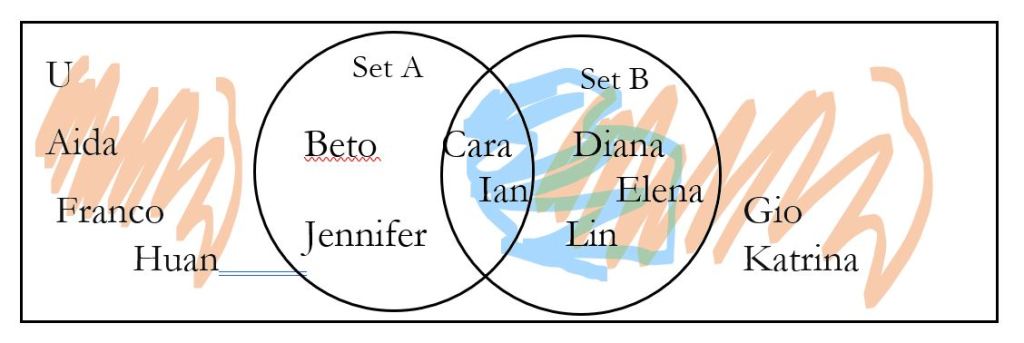
The intersection is where the two shadings overlap, where we have colored both colors. (In the picture, the place where both orange and blue are colored looks sort of green.)
Thus, A| ∩ B = students who do not like apples and are wearing blue shoes = {Diana, Elena, Lin}. To make it sound better, you might say, “do not like apples but they are wearing blue shoes,” but please show the translation with and in the homework.
Now you try: how would you translate A ∩ B| into words, using the same sets as above? What students would be in A ∩ B| ? Check your answer, here.
Think about how organizing sets like this helps you to think logically. This is the way your own students’ brains will grow when they sort more simple things, like buttons and shapes.

What groups do you see? Do you see any overlapping groups? You have now learned that the overlap is what is called the intersection of the two sets.