A 2.7 Solving Quadratic Equations by Graphing and by Factoring
Chapter 2 Section A7
Algebra Topics – Solving Quadratic Equations by Guess and Check, Graphing, or Factoring
Solving Quadratic Equations by Guess and Check and by Graphing
Quadratic equations are equations that have ![]() as the highest power of x. For example,
as the highest power of x. For example, ![]() is a quadratic equation, as is
is a quadratic equation, as is ![]() . To solve these equations, let’s first try the strategy of guess and check to see what will work to make the equation true.
. To solve these equations, let’s first try the strategy of guess and check to see what will work to make the equation true.
Example 1 For the equation 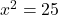 , what numbers will work?
, what numbers will work?
We can see that letting ![]() will make the equation true, because
will make the equation true, because ![]() . But another number will also make this equation true:
. But another number will also make this equation true: ![]() , because
, because ![]() . This means that the equation has two solutions.
. This means that the equation has two solutions.
Example 2 For the equation 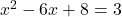 , what numbers will work?
, what numbers will work?
For the equation ![]() , the guessing is more difficult. We might first try guessing an easy number like zero:
, the guessing is more difficult. We might first try guessing an easy number like zero:
![]() , which is not correct, since we are trying to get 3. We can next try guessing higher or lower than 0. Since 1 is the next easiest number to try, let’s try that.
, which is not correct, since we are trying to get 3. We can next try guessing higher or lower than 0. Since 1 is the next easiest number to try, let’s try that.
![]() , which is correct!
, which is correct!
Since the other equation had two solutions, we can try to find a second solution for this equation as well. Some searching will reveal that the second number that works is x = 5.
Our guess and check is similar to making a table of points for the equation ![]() , and looking for when we get y = 3:
, and looking for when we get y = 3:

We see that there are two places (circled) where y = 3.
Example 3 For the equation 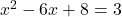 and the equation
and the equation 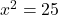 , where can we find the solutions on each graph?
, where can we find the solutions on each graph?
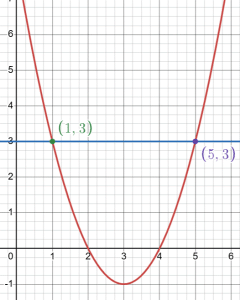
We can graph the equation ![]() using the table of points in the previous example to see where the graph passes through y = 3. Notice that a quadratic equation graphs a parabola shape, not a line, because squaring creates two possible solutions, as we saw from our guess and check work. The graph below shows the solution to
using the table of points in the previous example to see where the graph passes through y = 3. Notice that a quadratic equation graphs a parabola shape, not a line, because squaring creates two possible solutions, as we saw from our guess and check work. The graph below shows the solution to ![]() happens at (1,3) and (5,3). Thus the solutions are x = 1 and x = 5.
happens at (1,3) and (5,3). Thus the solutions are x = 1 and x = 5.
Similarly, a graph of ![]() shows two points where y = 25, at x = 5 and x = -5:
shows two points where y = 25, at x = 5 and x = -5:
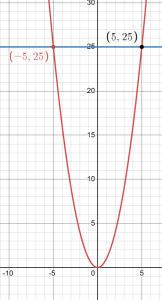
Thus, the solutions are x = 5 and x = -5.
Solving Quadratic Equations Using the Zero Factor Principle
Another way to solve a equation is to use the zero factor principle. Let’s look first at what the zero factor principle tells us.
If ![]() , then what do you know about what
, then what do you know about what ![]() must equal? What about
must equal? What about ![]() ?
?
You know that one of the two variables must be equal to zero. For example, we could have ![]() and
and ![]() , because
, because ![]() , or we could have
, or we could have ![]() and
and ![]() , because
, because ![]() . Or both a and b could equal zero, since
. Or both a and b could equal zero, since ![]()
Thus, if ![]() , then
, then ![]() must be zero, or
must be zero, or ![]() must be zero, or both.
must be zero, or both.
If two things multiply to equal zero, one or both of them must be zero.
Example 4 To use the zero factor prinicple with the equation 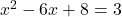 , we subtract 3 from both sides so that the equation is equal to zero:
, we subtract 3 from both sides so that the equation is equal to zero:
![]()
– 3 -3
We get ![]() .
.
Next, to solve, we need to factor the left side so that we have two factors (two things that are multiplied) that equal zero.
Reminder: to factor, set up ![]() because
because ![]()
Next, find two numbers that multiply to get positive 5 and add to get -6. The numbers -1 and -5 multiply to equal positive 5 and add to get -6.
We get
![]()
![]()
This means that either the first factor is equal to zero, or the second factor is equal to zero, or both, so ![]() or
or ![]() , or both.
, or both.
Solve each one:
![]()
+1 +1
![]()
![]()
+5 +5
![]()
These are the same x values we found in the table and on the graph.
To use this same idea with the equation ![]() , we subtract 25 from both sides so that the equation is equal to zero:
, we subtract 25 from both sides so that the equation is equal to zero:
We get ![]() .
.
Next, to solve, we need to factor the left side so that we have two factors (two things that are multiplied) that equal zero.
Reminder: to factor, set up ![]() because
because ![]()
Note: since there is no middle term, it might help to write the equation as ![]() , to show that the middle term is zero. So we are looking for two numbers that multiply to get -25 and add to get 0. The numbers 5 and -5 multiply to equal -25 and add to get 0.
, to show that the middle term is zero. So we are looking for two numbers that multiply to get -25 and add to get 0. The numbers 5 and -5 multiply to equal -25 and add to get 0.
![]() factors to
factors to
![]()
Using the zero factor principle, this means we know that ![]() or
or ![]() . Solve each:
. Solve each:
![]()
+5 +5
![]()
and
![]()
-5 -5
![]()
These are the same x values we found in our guess and check and on the graph.