A 1.1 – Algebra Extension: Introduction to Exponents and Rules for Exponents

Kathleen Offenholley; Fatima Prioleau

A 1.1 – Algebra Extension: Introduction to Exponents and Rules for Exponents

Chapter 1, Section A1

Algebra Topics – Introduction to Exponents and Rules for Exponents

Elementary Education – Connections to Base Ten

Base Ten

So far, we have learned about three base ten number systems: Traditional Chinese, Egyptian, and Hind Arabic (our system). What each of these have in common is that the powers of ten are a basis for the system. In this section, we’ll look at what we mean by “powers of ten” and at patterns of exponents in algebra.

The base ten place values begin with the ones place and continue with tens, hundreds, thousands, and so on. If we place these values in a table, we can begin to see some patterns.

Base ten place values

1

10

100

1,000

10,000

100,000

….

We notice that the number of zeros is increasing by one each time. This happens because each new value is ten times the previous one. Each time you multiply any whole number by ten, this adds on another zero.

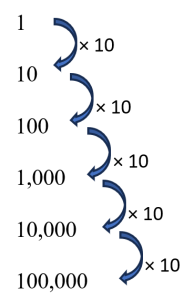
Graphing showing that each new place value is gotten by multiplying the previous one by ten

We can see that, by the time we get to 100,000, we have five factors of ten. That is 100,000 = 10 × 10 × 10 × 10 × 10. We can also write this as 10⁵, where 10 is the base and 5 is the exponent. If we have the number 600,000, we can write it as 6 × 100,000 = 6 × 10⁵. Notice that the 10 is the repeated factor.

A positive exponent means repeated multiplication. Writing this algebraically, $a^n=a\cdot a\cdot a\cdot a\ldots$ , where there are n factors of a. Note that when writing algebra, it is better to use a dot for multiplication, so that we don’t confuse it for the variable x.

Example 1 How can we evaluate 4 × 10³ without a calculator, by first expanding it? What are the repeated factors?

The exponent of 3 only applies to the 10 that it is directly next to, so 4 × 10³ = 4 × 10 × 10 × 10 = 4 × 1,000 = 4,000. Only the tens are repeated factors. Notice that the number of zeros matches the power of ten.

Example 2 How can we evaluate 5 × 2⁶ without a calculator, by first expanding it? What are the repeated factors?

5 × 2⁶ = 5 × 2 × 2 × 2 × 2 × 2 × 2 = 5 × 64 = 320. Notice that 2⁶ is not the same as 2 × 6 = 12. Instead, the 2 is repeatedly multiplied 6 times. The language can be confusing, so we might say “there are six factors of 2,” instead of how many “times” it’s multiplied.

Example 3 How can we evaluate (5 × 2)⁶ without a calculator, by first expanding it? What are the repeated factors?

Now, because we have parenthesis around 5 × 2, it is this whole expression that is repeated, so the repeated factor is 5 × 2. We could write this as:

(5 × 2)⁶ = (5 × 2) × (5 × 2) × (5 × 2) × (5 × 2) × (5 × 2) × (5 × 2) = 100,000. We could also think of this as:

(5 × 2)⁶ = 10⁶ = 100,000

Note that it’s generally fine to use a calculator to get the answers to examples 1 to 3, but we asked you not to on these to examples so that how you thought about them can help you with the algebra in the next example.

Example 4 How can we rewrite 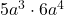$5a^3\cdot 6 a^4$ by first expanding it? Which parts are repeated factors?

Again, the exponent only applies to the variable it is directly next to, so we get $5\cdot a\cdot a\cdot a\cdot 6\cdot a\cdot a\cdot a\cdot a$ . When we have all multiplication, we can reorder it to be any order we like, so we can rewrite our expanded expression to have the two numbers together, and all the variables together. We get $5\cdot 6 \cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a$ . We know that 5 × 6 = 30. We also know how to rewrite the factors of a in exponential form. There are 7 of them, so we now have $30a^7$ . Thus, $5a^3\cdot 6a^4 = 30a^7$ .

Question: Now you try!

In example 4, you may notice a pattern of what happens to the exponents in your answer. We had $5a^3\cdot 6a^4 = 30a^7$ . What could you do with the exponents 3 and 4, to get the exponent of 7 in the answer?

spoiler space…

Also, look at the 5 and the 6 — what do you do to those to get the answer? Is it the same thing?

spoiler space…

Yes, you add the exponents! And the coefficients — the numbers in front of the variables — are multiplied (not added).

This happens because exponents tell you how many times something is being multiplied, which adds up. The coefficients of 5 and 6 are each just being multiplied once, so we multiply them by each other.

This leads us to the following rule for multiplying exponents: when multiplying exponential expressions that have the same base, add the exponents. Written algebraically, we have $a^m\cdot a^n = a^n^+^m$ .

Question: Now you try!

Now if the rule for multiplying exponents with the same base is to add the exponents, what do you think, logically, might be the rule for division? Make your conjecture now (a conjecture is “an educated guess”) and we will use the expanded form to see if your idea is correct!

Example 5 Use your idea for the rule of exponents for division to predict the answer to 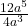$\frac{12a^5}{4a^3}$ , and check by writing the fraction in expanded form.

$\frac{12a^5}{4a^3}=\frac{4\cdot 3\cdot a\cdot a\cdot a\cdot a\cdot a}{4\cdot a\cdot a\cdot a}$

We know that $\frac{4}{4}=1$ . Similarly, $\frac{a}{a}=1$ .

So we can think of every time we have the same number or variable over the same number or variable, as equaling 1.

This gives us 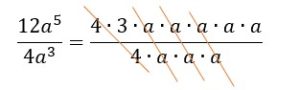$Shows a red line through the 4 on the top of the fractions and the 4 on the bottom, then a red line through a on the top matched with an a on the bottom$

Now we have $\frac{12a^5}{4a^3}=\frac{4\cdot 3\cdot a\cdot a\cdot a\cdot a\cdot a}{4\cdot a\cdot a\cdot a}=3\cdot a\cdot a=3a^2$

Did the answer come out the way you expected?

We ended up subtracting the exponents. But the coefficients of 12 and 4 were divided. You can think of 12 as 4 × 3 and cancel the common factor of 4, or you can think of 12 divided by 4 is 3.

This leads us to to the following rule for dividing exponents: when dividing exponential expressions that have the same base, subtract the exponents. Written algebraically, we have $\frac{a^m}{a^n} = a^n^-^m$ .

Question: Now you try!

For our next example, let’s see what happens when we take an expression that has exponents in it, and raise that whole expression to another power.

Example 6 How can we rewrite 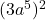$(3a^5)^2$ by first expanding it? Which parts are repeated factors?

First, try your own conjecture. What do you think will happen to the exponent of 5? Will it end up being added to the exponent of 2? Multiplied? Divided? What about the coefficient, 3? What is 3 raised to the second power?

To expand this expression, remember that the parenthesis tell us that the whole expression, $(3a^5)$ is being raised to the second power, which means that $3a^5$ is our repeated factor.

$(3a^5)^2 = 3a^5 \cdot 3a^5$

We can rearrange the factors so that we have $3\cdot 3 \cdot a^5 \cdot a^5$ . At this point, we can keep on expanding, and write out $3\cdot 3 a^5 \cdot a^5 = 3\cdot 3 a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot = 9a^1^0$ .

Now look at how our original problem and answer relate: $(3a^5)^2 = 3a^5 \cdot 3a^5 = 9a^1^0$ .

We notice that the exponent 5 is multiplied by the exponent 2, to get 10, while the coefficient is raised to the power of 2.

This leads us to the following rule for when we have an expression with an exponent, raised to another exponent: multiply the exponents. Written algebraically, we have $(a^m)^n = a^n^m$ .

Question: Now you try!

For these last examples, see if you can tell which rule of exponents you will need to use before you start simplifying. You may wish to refer to the Summary of Rules of Exponents at the bottom of the page.

Example 7 First, look at the summary of rules of exponents, and decide which rule of exponents we will need to simplify 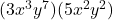$(3x^3y^7)(5x^2y^2)$ . Then simplify.

Since the problem shows two exponential expressions being multiplied, we will use the rule to add the exponents, keeping in mind that the coefficients (the number 3 and the number 5) still just get multiplied. $(3x^3y^7)(5x^2y^2) = 3 \cdot 5 x^3^+^2 y^7^+^2 = 15x^5y^9$

Example 8 First, look at the summary of rules of exponents, and decide which rule of exponents we will need to simplify 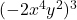$(-2x^4y^2)^3$ . Then simplify.

Here it is worth reminding ourselves that a negative number × a negative number = a positive. We have (-2)³ = -2 × -2 × -2. The first two multiply together to give us +4, then multiply by -2 to get a negative again, 4 × -2 = -8

Example 9 First, look at the summary of rules of exponents, and decide which rule of exponents we will need to simplify 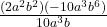$\frac{(2a^2b^2)(-10a^3b^6)}{10a^3b}$ . Then simplify.

This problem has both multiplication and division, so we will need to add exponents when there are multiplied exponential expressions, and subtract exponents when the exponential expressions are divided, keeping in mind that the coefficients get multiplied and divided in the usual way.

When we have multiplication and division mixed together, we go from left to right, starting at the top of the fraction (more on the order of operations is in the next algebra extension). So we start by multiplying the coefficients and adding the exponents in the numerator (top) of the fraction. $\frac{(2a^2b^2)(-10a^3b^6)}{10a^3b} = \frac{2 \cdot -10 a^2^+^3 b^2^+^6}{10a^3b}= \frac{-20 a^5 b^8}{10a^3b}$
Note that we have a positive number multiplied by a negative one, which gives us a negative.

Now we can divide. Think about what -20 ÷ 10 is, and then remember that the rule for dividing expressions with exponents is to subtract them. It’s also important to note that when we have just plain b, without an exponent, that’s the same as b¹.

We get $\frac{-20 a^5 b^8}{10a^3b}= -2 a^5^-^3 b^8^-^1=-2a^2b^7$

Important Note The way we did this last problem is not the only way to do it!

You might have noticed in the beginning of $\frac{(2a^2b^2)(-10a^3b^6)}{10a^3b}$ that the two tens — one in the numerator and one in the denominator could be “cancelled” leaving -1, since 10/-10 = -1. Similarly, since a³ is in both numerator and denominator, we could have also cancelled those. There are often several correct ways to simplify these problems. The important part is that any of these methods, including expanding everything out — should come to the same conclusion.

Question: Now you try!

Summary of Rules of Exponents from this Section

Here are the rules we discovered in this section:

Positive exponents indicate repeated multiplication. Written algebraically, 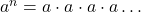$a^n=a\cdot a\cdot a\cdot a\ldots$ , where there are n factors of a. Tip: If we have an expression in parenthesis raised to an exponent, the whole expression is repeated, so any coefficient inside the parenthesis is raised to that power. For example, 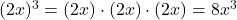$(2x)^3 = (2x) \cdot (2x) \cdot (2x) = 8x^3$ . So the 2 ends up raised to the third power.
When multiplying exponential expressions that have the same base, add the exponents. Written algebraically, we have 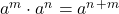$a^m\cdot a^n = a^n^+^m$ . Tip: if there are coefficients in front of the variables, they still get multiplied. For example, $3x^7\cdot 4x^2 = 12x^9$ .
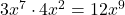When dividing exponential expressions that have the same base, subtract the exponents. Written algebraically, we have 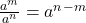$\frac{a^m}{a^n} = a^n^-^m$ . Tip: if there are coefficients in front of the variables, they still get divided. For example, $\frac{15x^7}{3x^2} = 5x^5$ .
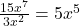When we have an exponential expression raised to another exponent, we multiply the exponents. Written algebraically, we have 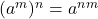$(a^m)^n = a^n^m$ . Tip: if there are coefficients in front of the variables, they still get raised to that exponent. For example,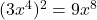 $(3x^4)^2 = 9x^8$

Instead of memorizing these as rules, remember that each one of them should make sense. It’s always okay to expand the expression to check if your interpretation is correct. It is so important that math should make sense, and that you do not just blindly follow the rules someone told you. It is fine to slow down, take your time, and reason your way to the correct answer. After all, reasoning is what math is supposed to be about.

Remember: the fastest person is not the one who is “best” at math!

Finally, think about how when children first learn to count and to add and subtract, they count on their fingers — most don’t get quick at addition and subtraction for a while. That’s fine — that’s why our numeration system evolved as base ten, because we have ten fingers!

It’s so important to take the time to understand, and to give your students that time, too.

Homework

Video help can be found, here. Please back up the video to the beginning.

The homework below is a pdf of the online homework available in https://imathas.helpyourmath.com/. It does not include answers. Note that it is in two parts. In the first part, the homework contains images for each homework; the second part is text, to make the problems accessible to screen readers. Algebra extension homework A1

If you wish to use the online imathas.helpyourmath system instead, your instructor must create a course for your class and give you a key to it. If you are studying the algebra on your own (not for class credit), and would like access to the system, please email Dr. Kathleen Offenholley, koffenholley@bmcc.cuny.edu or kathleenOffenholley@yahoo.com, for access to her course.

Unless otherwise specified, images in this section are by Kathleen Offenholley and licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

Chapter 1, Section A1

Base Ten

Base ten place values

Example 1 How can we evaluate 4 × 103 without a calculator, by first expanding it? What are the repeated factors?

Example 2 How can we evaluate 5 × 26 without a calculator, by first expanding it? What are the repeated factors?

Example 3 How can we evaluate (5 × 2)6 without a calculator, by first expanding it? What are the repeated factors?

Example 4 How can we rewrite by first expanding it? Which parts are repeated factors?

Example 5 Use your idea for the rule of exponents for division to predict the answer to , and check by writing the fraction in expanded form.

Example 6 How can we rewrite by first expanding it? Which parts are repeated factors?

Example 7 First, look at the summary of rules of exponents, and decide which rule of exponents we will need to simplify . Then simplify.

Example 8 First, look at the summary of rules of exponents, and decide which rule of exponents we will need to simplify . Then simplify.

Example 9 First, look at the summary of rules of exponents, and decide which rule of exponents we will need to simplify . Then simplify.

Important Note The way we did this last problem is not the only way to do it!

Summary of Rules of Exponents from this Section

Homework

License

Share This Book

Example 1 How can we evaluate 4 × 10³ without a calculator, by first expanding it? What are the repeated factors?

Example 2 How can we evaluate 5 × 2⁶ without a calculator, by first expanding it? What are the repeated factors?

Example 3 How can we evaluate (5 × 2)⁶ without a calculator, by first expanding it? What are the repeated factors?

Example 4 How can we rewrite $5a^3\cdot 6 a^4$ by first expanding it? Which parts are repeated factors?

Example 5 Use your idea for the rule of exponents for division to predict the answer to $\frac{12a^5}{4a^3}$ , and check by writing the fraction in expanded form.

Example 6 How can we rewrite $(3a^5)^2$ by first expanding it? Which parts are repeated factors?

Example 7 First, look at the summary of rules of exponents, and decide which rule of exponents we will need to simplify $(3x^3y^7)(5x^2y^2)$ . Then simplify.

Example 8 First, look at the summary of rules of exponents, and decide which rule of exponents we will need to simplify $(-2x^4y^2)^3$ . Then simplify.

Example 9 First, look at the summary of rules of exponents, and decide which rule of exponents we will need to simplify $\frac{(2a^2b^2)(-10a^3b^6)}{10a^3b}$ . Then simplify.