A 1.3 – Algebra Extension: Adding and Subtracting Polynomials
Chapter 1, Section A3
Algebra Topics – Adding and Subtracting Polynomials
Elementary Education – Connections to Adding in Base Ten
Polynomial Addition and Subtraction
As we saw in the previous section, adding polynomials is very similar to adding using partial sums addition in base ten. We looked at the example 397 + 528, which is similar to adding (3x2 + 9x + 7) + (5x2 + 2x + 8):
| 3x2 + 9x + 7 | 397 = 300 + 90 + 7 |
| + 5x2 + 2x + 8 | +528 = 500 + 20 + 8 |
| 8x2 + 11x + 15 | 800 + 110 + 15 |
We also noted that if we let x = 10 in each expression in (3x2 + 9x + 7) + (5x2 + 2x + 8), we get 397 + 528.
Just as children can begin to understand addition and subtraction using base ten blocks and partial sums addition, students studying algebra can use algebra tiles to understand basic facts about polynomials. Algebra tiles look very similar to base ten blocks. There is a unit block, like the ones place. The next sized block is a rod or bar, just like in base ten, but instead of it being ten blocks tall, it is x blocks tall. The square is then an x by x block which represents x • x = x2 instead of 102 = 100, and the largest is the cube, x • x • x = x3, instead of 103 = 1,000.
Algebra Tiles
| x3 | x2 | x | 1 |
| x, cubed | x, squared | x | units |

x units tall x units deep x units wide
|

x units tall x units wide |
x units tall one unit wide |
1 unit wide |
Example 1 Represent 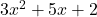 using algebra tiles.
using algebra tiles.
We would use 3 of the ![]() tiles, 5 of the
tiles, 5 of the ![]() tiles, and 2 ones.
tiles, and 2 ones.



![]()
![]()
![]()
![]()
![]()
![]()
![]()
Example 2 Represent 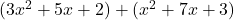 using algebra tiles.
using algebra tiles.
As we did in the previous section, with base ten block, we can add these algebra tiles. Notice that ![]() means just one x2 algebra tile. We can choose to write this as
means just one x2 algebra tile. We can choose to write this as ![]() or as
or as ![]() .
.



![]()
![]()
![]()
![]()
![]()
![]()
![]()
+

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We have a total of 4 of the square blocks. Combining all the long x blocks, we get 12 of them. Adding the units, 2 units + 3 units = 5 units.
Thus, we get an answer of ![]() .
.
This is very similar to adding with base ten blocks but we don’t finish the addition by making any trades — for example, we do not trade 10 of the 12 x blocks for a square, x2 block. Why not? Because we don’t know whether or not 10 of the long blocks are equal to a square block. We don’t what x is. The value of x could be anything — it could be ten, or 3, or any other number.
Example 3 What happens when we let x = 10 in our previous question and result, 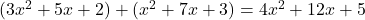 ? What if we instead let x = 4?
? What if we instead let x = 4?
Let x = 10
| Let x = 10 on the left side by replacing each x with 10.
|
Let x = 10 on the right side by replacing each x with 10.
|
|
| Simplify each side by raising 10 to the second power, and then multiply.
|
|
|
| Add.
|
If we let x = 10, we end up with both sides of the equation equaling 525.
What about if x = 4?
Let x = 4
| Let x = 4 on the left side by replacing each x with 4.
|
Let x = 4 on the right side by replacing each x with 4.
|
|
| Simplify each side by raising 4 to the second power, and then multiply.
|
|
|
| Add.
|
If we let x = 4, we end up with both sides of the equation equaling 117.
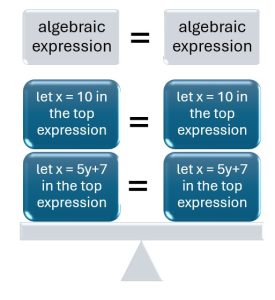
In general, when you are simplifying or operating on an algebraic expression, if you substitute a number into the original expression, you should get the same result when you substitute that number into the equivalent expression. The image on the rights shows two equal algebraic expression that are still equal if we let x = 10 in each one. They are even still equal if you let x be something complicated, like 5y + 7. The two expressions will be equal, no matter what we substitute for x.
This idea, that if two expressions are equal, they should be equal no matter what x is, is one of the powerful things about algebra — it can tell us general truths about how numbers work.
Example 4 Represent 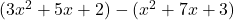 using algebra tiles.
using algebra tiles.
Here, since we are subtracting, we can represent the bottom set of blocks in a different color, to show that they are each being subtracted. We have



![]()
![]()
![]()
![]()
![]()
![]()
![]()
+

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Notice that there is now a + sign between the two sets of tiles. This is because we have changed the subtraction into adding the negative tiles, so that we have ![]()
With algebra tiles, when we add a positive tile to a negative tile, they cancel each other out, leaving zero. For example, ![]() +
+ ![]() = 0. This is because
= 0. This is because ![]() .
.
Similarly, ![]() +
+![]() =0 because
=0 because ![]() . The squares work in the same way because
. The squares work in the same way because ![]() , as do the cubes.
, as do the cubes.
In this particular problem, we have two blue units and three yellow units to combine. We can pair a blue one with a yellow one to cancel them and see what is left:
![]()
![]()
![]()
![]()
![]()
When we cancel the opposite color tiles, we get:
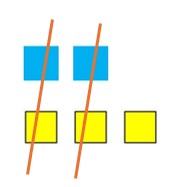
Now we have one yellow unit left. This illustrates that ![]() .
.
For adults, money is often a good way to model positive and negative numbers. If we have $2 and spend $3, we now owe $1. We can thinking of spending and owing as negative.
For the x terms, we have ![]() . Again, we can visualize the canceling blocks, or spending money.
. Again, we can visualize the canceling blocks, or spending money.
I have $5 and spend $7, now I owe $2.
Or, using the blocks, we have
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We “cancel” the opposite color tiles to get
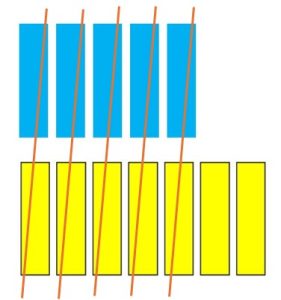
Now we have two negative tiles left. Thus, ![]() .
.
And finally, with the ![]() blocks, we have
blocks, we have ![]() (or we can leave out the 1 in front of
(or we can leave out the 1 in front of ![]() if we like)
if we like)
You can imagine the blue and yellow squares cancelling, with two blue squares left, or you can think: I have $3 and spend $1, so now I have $2.
Example 5 Represent 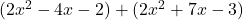 using algebra tiles.
using algebra tiles.
Now we are adding with a mix of positive and negative coefficients. Again, we can use a different color tile to represent the negative ones. Here, we choose blue for positive tiles and yellow for negative ones.


![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Before you see the worked out answer, see if you can visualize which tiles will cancel (equal zero), and which will not. Remember that tiles only cancel if they are opposite colors.
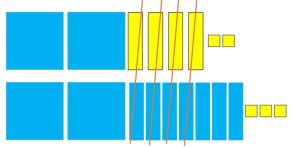
We can see that none of the blue squares cancel, so we have a total of 4 of them, or ![]() .
.
With the x‘s we can see that 4 of them cancel out, leaving us with 3 blue (positive) bars, so we have ![]() .
.
With the units, we have two yellow ones plus three yellow ones. Nothing cancels out, so we end up with 5 yellow units. This means that ![]() . In other words, if I owe $2 and I borrow $3 more, I now owe $5. Notice that adding two negatives does not mean they “cancel” each other out! (If you thought they did, you may be thinking of the rule for multiplication.)
. In other words, if I owe $2 and I borrow $3 more, I now owe $5. Notice that adding two negatives does not mean they “cancel” each other out! (If you thought they did, you may be thinking of the rule for multiplication.)
Thus we have: ![]()
Example 6 Represent  using algebra tiles.
using algebra tiles.
Notice that this problem is similar to example 5, but now instead of adding the second expression, we are subtracting it. Think of how we would represent that we are doing the opposite operation in example 6. Each of the second row of tiles should be in the opposite color from what it was in the previous problem.
Some key points to remember when subtracting a polynomial:
- Subtracting a polynomial is the same as adding the opposite of each term.
- Using algebra tiles, this means that each tile being subtracted is the same as adding the opposite color.
- The negative in front of the parenthesis changes the sign of each term inside the parenthesis.
Notice that these three points are all just different ways of saying the same thing.
Now we have:
![]() .
.
The positive ![]() changes to negative, since it is being subtracted.
changes to negative, since it is being subtracted.
The positive ![]() changes to negative, since it is being subtracted.
changes to negative, since it is being subtracted.
The negative 3 at the end changes to positive 3 because ![]() . Or, you can think of the algebra tile changing to the opposite color. Remember that subtracting a polynomial changes every tile to its opposite.
. Or, you can think of the algebra tile changing to the opposite color. Remember that subtracting a polynomial changes every tile to its opposite.
Now we have:


![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now we can see that the ![]() terms cancel. We get a total of 11 yellow (negative) x bars, since nothing cancels. For the units, two of them cancel and we are left with one blue, positive unit. This gives us
terms cancel. We get a total of 11 yellow (negative) x bars, since nothing cancels. For the units, two of them cancel and we are left with one blue, positive unit. This gives us ![]() .
.
Or, without using the algebra tiles, looking just at the algebraic expression, we have ![]() Bringing the “like terms” (same algebra tiles) together, we get
Bringing the “like terms” (same algebra tiles) together, we get ![]() .
.
The most difficult part of this may be that subtracting negative 3 is the same as adding 3, that is ![]() . Here, it may help to think about how the opposite of three yellow blocks is three blue blocks, or it may be easier to think of money. If I owe someone $3, and they tell me I don’t owe them after all, it’s like taking away a debt of $3, so now I have $3 more than I thought!
. Here, it may help to think about how the opposite of three yellow blocks is three blue blocks, or it may be easier to think of money. If I owe someone $3, and they tell me I don’t owe them after all, it’s like taking away a debt of $3, so now I have $3 more than I thought!
It is fine to imagine or sketch out the algebra blocks each time, or to think of money each time, or to rely solely on the written form of the algebraic expression, or a combination of the three — whatever makes it easier for you to understand and remember.
Example 7 Represent  using algebra tiles.
using algebra tiles.
We actually can’t represent this whole expression using algebra tiles! It is not possible to make ![]() using algebra tiles, because the largest type of block you can make is a three-dimensional block, x3, which is a cube. Base ten blocks have a similar issue — the largest power of ten that you can represent is 103 = 1,000. For problems that can’t be represented with blocks, we hope that all the previous work with the block models leads to a deeper understanding of doing the arithmetic or algebra, so that such problems can be done without the models.
using algebra tiles, because the largest type of block you can make is a three-dimensional block, x3, which is a cube. Base ten blocks have a similar issue — the largest power of ten that you can represent is 103 = 1,000. For problems that can’t be represented with blocks, we hope that all the previous work with the block models leads to a deeper understanding of doing the arithmetic or algebra, so that such problems can be done without the models.
For this question, we can use our previous work with the tiles to remember that everything in the expression being subtracted is the same as adding the opposite. In other words, the negative in front of the parenthesis changes the sign of each term inside the parentheses. ![]() becomes
becomes ![]() . Then when we combine
. Then when we combine ![]() we can still think of the 5 blue blocks canceling 5 of the yellow blocks, even if we can’t draw them, or we can think of having $5 and spending $8. We end up with
we can still think of the 5 blue blocks canceling 5 of the yellow blocks, even if we can’t draw them, or we can think of having $5 and spending $8. We end up with ![]() . There is nothing to combine the
. There is nothing to combine the ![]() with, so we leave it alone. Next we have
with, so we leave it alone. Next we have ![]() . For the next one,
. For the next one, ![]() , you might remember that if there are 9 yellow blocks and 7 more yellow blocks, you now have 16 yellow blocks, or you might think of being $9 in debt and borrowing $7 more — now you owe $16, or
, you might remember that if there are 9 yellow blocks and 7 more yellow blocks, you now have 16 yellow blocks, or you might think of being $9 in debt and borrowing $7 more — now you owe $16, or ![]() , and finally, 5 + 8 = 13.
, and finally, 5 + 8 = 13.
Putting all these steps together, we have
![]()
Distribute the negative: ![]()
Put like terms together: ![]()
Combine like terms: ![]()
The steps above show a much faster way to work on the problem. When you get faster at doing these, you may wonder why you ever bothered going through these slowly using blocks or thinking about money each step of the way. The point of the slow, thoughtful approach is so that you can understand, and so that the easier, quicker way will make sense to you. Similarly, there will be children who will be able to see how to add quickly, and will not need the base ten blocks for long, while others will want to use them for a long time. Either way should be fine, so long as students understand what they are doing.
Now that we have done some work to understand positive and negative numbers, let’s do a problem with exponents, and let our deeper understanding help us figure out how to tackle more difficult problems.
Example 8 Simplify 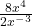 and write using positive exponents.
and write using positive exponents.
Remember that when we divide exponential expressions with the same base, we subtract them. So we have ![]() . And now we have a better understanding of what -(-3) means, that it is reversing the color of three negative blocks, or canceling a debt of $3. We know why we can change it to +3. So now we have
. And now we have a better understanding of what -(-3) means, that it is reversing the color of three negative blocks, or canceling a debt of $3. We know why we can change it to +3. So now we have ![]() . Notice that the number 2 stays where it is, because it does not have a negative exponent.
. Notice that the number 2 stays where it is, because it does not have a negative exponent.
Another way to think of the problem ![]() , is that a negative exponent in the denominator can be brought up to the numerator and made positive. That is,
, is that a negative exponent in the denominator can be brought up to the numerator and made positive. That is, ![]() . This is often used as a short cut and is possible because subtracting a negative gives a positive.
. This is often used as a short cut and is possible because subtracting a negative gives a positive.
Remember that a negative exponent is not the same as a negative number! To see this visually, use the slider below to change the base and exponent. When is the value negative? Does sliding the exponent make the value negative? What about sliding the base value?
Unless otherwise specified, images in this section are by Kathleen Offenholley and licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.