A 2.1 Algebra Extension: What is a Variable? Writing and Solving Equations
Chapter 2 Section A1
Algebra Topics – What is a Variable? Writing and Solving Equations
Elementary Education – Making and Discovering Block Patterns
What is a Variable?
| Dear Algebra,
Please stop asking us to find your X. She’s not coming back and don’t ask Y. |
People often think of a variable as “the answer.” For example, if you are asked to “solve for ![]() ” or “find
” or “find ![]() ” in the equation
” in the equation ![]() , the answer is
, the answer is ![]() .
.
But a variable is much, much more than that!
Definition. A variable is a placeholder for a mathematical object. The object can be any kind of number, a set of numbers, or even an expression.
For example, the variable ![]() could equal 3,
could equal 3, ![]() , 0.68,
, 0.68, ![]() , the set of numbers {0, 1,2,3,4,5…}, or even the expression
, the set of numbers {0, 1,2,3,4,5…}, or even the expression ![]() .
.
For this section, we’ll focus on the variable as a set of numbers. We’ll use the idea that in a number pattern, the variable can be a placeholder for the the number that varies. We’ll use blocks to help us see the variables. Using blocks, or cubes, or other objects to model patterns is also important in elementary education, as we have seen in the previous sections when we looked at adding to ten facts, and adding and subtracting in base ten. For young children, even just gathering ten objects into a cup is an important way to visualize the number.
Example 1 What pattern do you see in the blocks below? Which part is changing (varying) and which part is staying the same? Use the pattern to figure out how many blocks will be in the 100th tower.
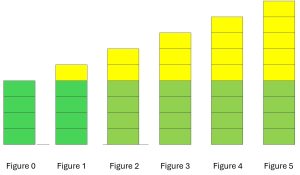
Notice that there are always 4 green blocks, and the amount of yellow blocks is what is changing, or varying.
Figure 0 = 4
Figure 1 = 4 + 1 = 5
Figure 2 = 4 + 2 = 6
Figure 3 = 4 + 3 = 7
Figure 4 = 4 + 4 = 8
Figure 5 = 4 + 5 = 9
Notice also that the number of blocks being added is the same as the figure number. The 100th figure will have 4 + 100 = 104 blocks.
The number that varies is the number being added to 4. This will be our variable. We can use any letter we like for that variable. Let’s use x, this time. We get the expression, 4 + x. Notice that the total number of blocks, also varies. We can use another variable for the total number of blocks, y.
We can also write this as a table, to help us see the pattern more clearly:
| Figure number, x | Total number of blocks, y |
| 0 | 4 |
| 1 | 5 |
| 2 | 6 |
| 3 | 7 |
| 4 | 8 |
| 5 | 9 |
| … | |
| 100 | ? |
We can add a column to our table to see how the figure number relates to the total number of blocks.
| Figure number, x | pattern | Total number of blocks, y |
| 0 | 4 + 0 = | 4 |
| 1 | 4 + 1 = | 5 |
| 2 | 4 + 2 = | 6 |
| 3 | 4 + 3 = | 7 |
| 4 | 4 + 4 = | 8 |
| 5 | 4 + 5 = | 9 |
| … | ||
| 100 | 4 + 100 = | 104 |
| x | 4 + x = | y |
From the table we can use the pattern to see that the 100th figure number would have 104 blocks. In general, for any figure number, x, we have 4 + x = y. Since the order of addition doesn’t matter, we can also write x + 4 = y, or y = x + 4. Here, the variable x, stands for any whole number.
Another way to find the 100th block pattern is to let x = 100 in our equation, x + 4 = y, which gives us 100 + 4 = 104, so, y = 104.
Example 2 What pattern do you see in the blocks below? Which part is changing (varying) and which part is staying the same? How does the number of new blocks relate to the figure number? Use the pattern to figure out how many blocks will be in the 100th figure.
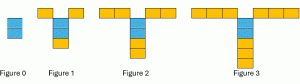
Before you try to figure out the numbers, try to describe in words what you see happening to the figure each time. You might imagine you see a shirt, or a tree, or anything else. Think about what is growing on it each time.
You might see that figure 0 has no arms, and figure 1 has three arms. Figure 2 still has three arms, as does figure 3, but now each arm is longer.
How we see the figure will make us interpret it differently. We might say Figure 1 = 2 + 1 + 1 + 1, Figure 2 = 2 + 2 + 2 + 2, and Figure 3 = 2 + 3 + 3 + 3; or we might say that Figure 1 = 2 + 1 × 3, Figure 2 = 2 + 2 × 3, and Figure 3 = 2 + 3 × 3. We might also just notice how much is added on each time. Figure 1 = 2 + 3, Figure 2 = 2 + 6, and Figure 3 = 2 + 9. All these interpretations are correct.
We can also write this as a table, to help us see the pattern more clearly:
| Figure number, x | Total number of blocks, y |
| 0 | 2 |
| 1 | 5 |
| 2 | 8 |
| 3 | 11 |
Again, let’s add a new column to help us see the pattern.
| Figure number, x | pattern | Total number of blocks, y |
| 0 | 2 + 0 = | 2 |
| 1 | 2 + 1 + 1 + 1= | 5 |
| 2 | 2 + 2 + 2 + 2 = | 8 |
| 3 | 2 + 3 + 3 + 3 = | 11 |
Does the table help you to see what’s happening to the figure number, x? Maybe you can now use the pattern to find the 100th figure.
For the 100th figure, we would have 2 + 100 + 100 + 100 = 302. Another way to write this would be 2 + 3 × 100.
Notice that the figure number is being added on three times, which we can also write as being multiplied by 3.
This pattern can now help us find the equation for the number of blocks.
| Figure number, x | pattern | Total number of blocks, y |
| 0 | 2 + 0 = | 2 |
| 1 | 2 + 3 × 1= | 5 |
| 2 | 2 + 3 × 2 = | 8 |
| 3 | 2 + 3 × 3 = | 11 |
| … | ||
| 100 | 2 + 3 × 100 = | 302 |
| x | 2 + 3x | y |
So we now have the equation, 2 + 3x = y.
Example 3 Try this pattern on your own, going all the way from the starting number of blocks to figuring out what the 100th block would be. Finally, write the equation for the number of blocks. Write a table to help you see the relationship.
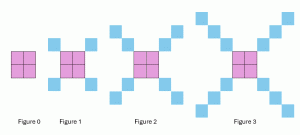
| Figure number, x | pattern | Total number of blocks, y |
| 0 | 4 + 0 = | 4 |
| 1 | 4 + 4 × 1= | 8 |
| 2 | 4 + 4 × 2 = | 12 |
| 3 | 4 + 4 × 3 = | 16 |
| … | ||
| 100 | 4 + 4 × 100 = | 402 |
| x | 4+ 4x | y |
So we now have the equation, 4 + 4x = y.
Solving for a Variable
If the previous examples, the variable x could take on many different values. In this context of block patterns, when would x have only one value? The variable would have only one value if we asked a question such as, “When does that pattern have 30 blocks?”
Example 4 When will the pattern below have 30 blocks?

To find when the pattern has 30 blocks, we could count using just the figures, or use the table to find where the number of blocks is 30.
| Figure number, x | Total number of blocks, y |
| 0 | 4 |
| 1 | 5 |
| 2 | 6 |
| 3 | 7 |
| 4 | 8 |
| 5 | 9 |
| … | |
| ? | 30 |
Now we are looking for when y is 30. We can count our way there, or we can use the equation x + 4 = y, and let y = 30. Now we have x + 4 = 30. What number could x be, so that y is 30?
If x = 26, we have 26 + 4 = 30. So the 26th figure will have 30 blocks.
We could also solve to find x, a process with which you are probably familiar:
x + 4 = 30
– 4 -4
x = 26
We solve the equation by subtracting 4 from both sides of the equation, to get x = 26. The 26th figure will have 30 blocks. Notice that in solving, we do the opposite of what is being done to the variable. Since 4 is being add to x, we subtract 4 to solve for x.
Example 5 When will the pattern below have 44 blocks?

Again, we can use the table to count our way to 44 blocks.
| Figure number, x | pattern | Total number of blocks, y |
| 0 | 2 + 0 = | 2 |
| 1 | 2 + 3 × 1= | 5 |
| 2 | 2 + 3 × 2 = | 8 |
| 3 | 2 + 3 × 3 = | 11 |
| … | ||
| ? | 2 + 3 × ? = | 44 |
| x | 2 + 3x | y |
Or we can solve the equation, 2 + 3x = y, with y = 44.
This means we need to solve 2 + 3x = 44
We solve by first subtracting 2:
2 + 3x = 44
-2 -2
3x = 42 then we divide by 3
÷3 ÷3
x = 14
So, the 14th figure will have 44 blocks.
We will talk more about why equations are solved this way a few sections later in this text. For now, note that we usually solve equations by removing any thing that is being added to or subtracted from the variable first, by doing the opposite operation, then we undo multiplication and division, again by using the opposite operation.
Example 6 When will the pattern in example 4 have 60 blocks?
This time, we can go directly to solving.
We need to solve the equation, 2 + 3x = y, with y = 60.
This means we need to solve 2 + 3x = 60
Since the 2 is adding to 3x, we solve by first by doing the opposite and subtracting 2:
2 + 3x = 60
-2 -2
3x = 58 And then since the 3 is multiplying the variable, x, we divide by 3
÷3 ÷3
x = 19.3333…
But there is no such figure number as 19.3333…. ! Since the figure numbers are only whole numbers, the answer must be that there is no such figure.
In many problems, x can take on any value — fractions, decimals, square roots, x can even be an expression like 2z+4. But in this particular problem, x must be a whole number.
Unless otherwise specified, images in this section are by Kathleen Offenholley and licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.