Sec. 2.2 – Multiplication as Area; Commutative and Distributive Properties; Slope
Chapter 2, Section 2
Math Topics – Commutative and Distributive Properties, Slope in Successive Differences and Arithmetic Sequences
Elementary Education – Multiplication as Area; Alternate Methods of Multiplication and Division
Multiplication as Groups and Arrays
Multiplication can be modeled as groupings of objects. For example, 2 × 5 can be illustrated as 2 groups of 5 objects each:
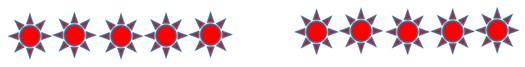
Or we can make 5 groups, each with two objects:

Multiplication is commutative, that is, you can multiply two numbers in any order to get the same result. Thus, two groups of 5 objects in each group each gives the same result as five groups of 2 objects in each group. Algebraically, we write: a × b = b × a, or ab = ba.
Question to think about: Is addition commutative? What about subtraction? Division?
When we group the objects together into rows, we can see the multiplication as an array. We can also see the commutative property in the array, by noticing that we have 5 columns with 2 stars each, or 2 rows with 5 stars each. When children group objects in rows and columns, this helps them visualize the commutative property, that 2 × 5 is the same as 5 × 2.

Multiplication as Area
Multiplication can also be thought of as the area of a rectangle. The 2 by 5 rectangle below has an area of 10. We can count that there are 10 squares inside it.
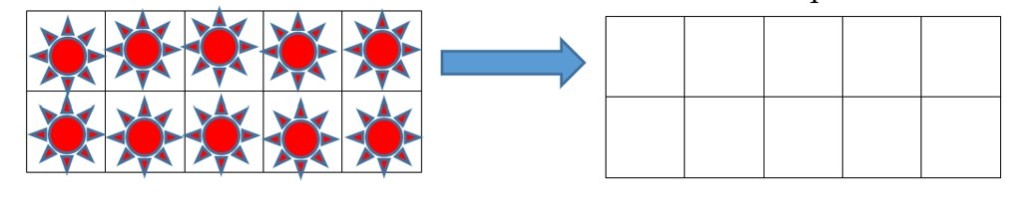
We can use the area model for larger multiplication problems as well.
The rectangle below is 14 across the top and 12 down, so it has an area of 14 × 12 = 168. This means that we can count that there are 168 squares inside it.
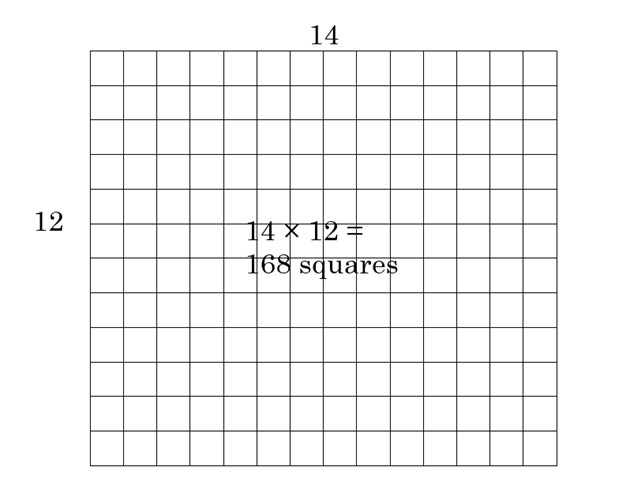
We can fill in the area with base ten blocks. Start by placing a 10 by 10 flat into the rectangle, in the top left corner:
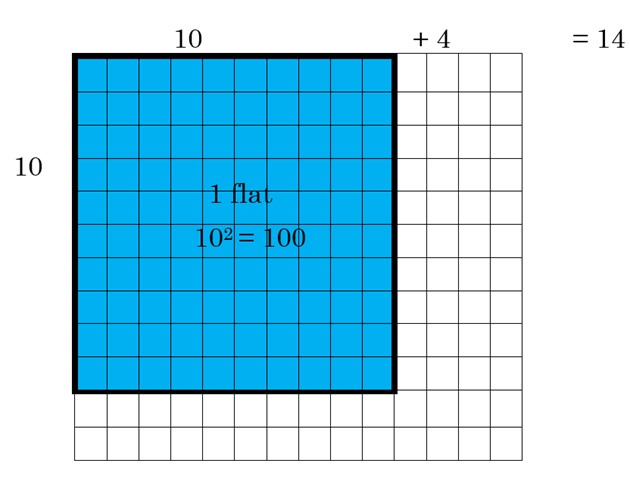
Can we fit any more flats into the rectangle? No. But we can fit some rods, on each side of the flat. See if you can do this on your own, before continuing. How many rods can you place to the right of the flat? Remember that a rod is ten units tall by one unit wide. How many rods can you place underneath the flat? Now think of the rod as being ten units long and one unit wide!
After you fill in the rods, see how many units you have in the space that is left.
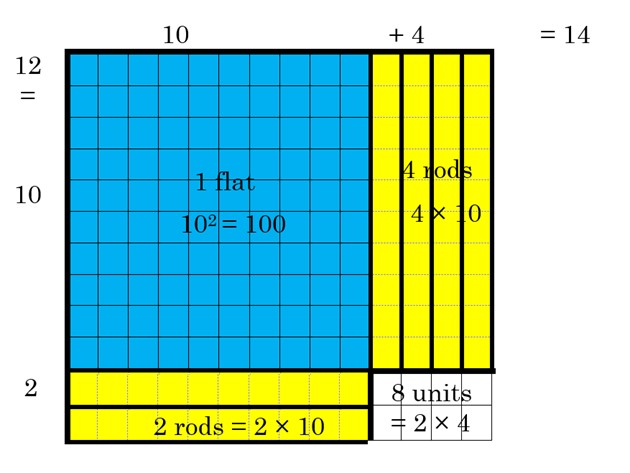
Thus, the area for a 14 by 12 square is the same as
1 flat + 4 rods + 2 rods + 8 units = 100 + 40 + 20 + 8 = 168.
This is the same as what we get when we multiply 14 × 12.
Partial Products Multiplication
Multiplication can be broken down into separate place values, similarly to addition and subtraction. For example, the multiplication above, 14 × 12, can be written as
(10 + 4) × (10 + 2). We can then use the distributive property, either vertically or horizontally, to multiply:
10 + 4
× 10 + 2
20 + 8 ← in this row, each top number has been multiplied by 2
100 + 40 ← in this row, each top number has been multiplied by 10
100 + 60 + 8 = 168
Notice that each of the partial products corresponds to the flats rods and units in our area model: 100 + 40 + 20 + 8 = 1 flat + 4 rods + 2 rods + 8 units
Horizontally, we can write 14 × 12 = (10 + 4)(10 + 2) = 100 + 20 + 40 + 8. The arrows below show which numbers are being multiplied together.
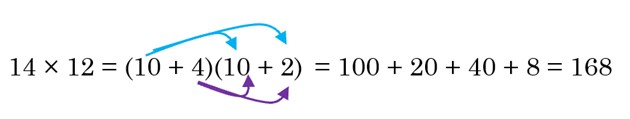
This is like using the distributive property to multiply the binomials ![]() . The arrows below show which terms are being multiplied together.
. The arrows below show which terms are being multiplied together.
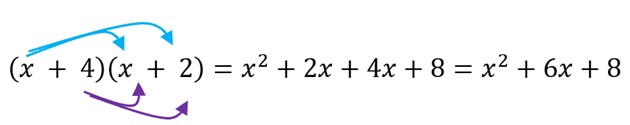
Many people prefer writing and multiplying binomials horizontally (and multiplying across), while many others prefer stacking them and multiplying vertically (going down). Neither method is inherently better than the other, it often just depends on what you are used to.
Using base ten blocks and the area method of multiplication, along with partial products multiplication, can be a way to introduce students to multiplication with larger numbers. It can be a way to get students to understand the meanings behind the shorter multiplication algorithm, since the two methods are really very similar.
| 10 + 4 | 14 | |
| × 10 + 2 | × 12 | |
| 20 + 8 | 28 | |
| 100 + 40 | 140 | |
| 100 + 60 + 8 = 168 | 168 |
Example 1 Show 24 × 15 a.) Use the area method and base ten blocks b.) Use partial products c.) Show the similar binomial multiplication ![]()
1a.) To use the area method and base ten blocks, begin by counting out 24 squares across and 15 squares down, or 15 across and 24 down – either way will result in the same area, since multiplication is commutative.
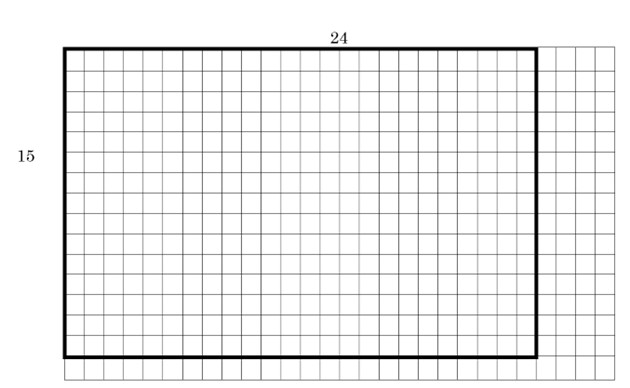
Next, we look to fill as many flats as we can, starting in the top left corner.

We can fit in two 10 by 10 flats. The rods will line up next to the flats, because rods are 10 long by 1 across. Before you continue reading, see if you can see how many rods you will need, both to the right of the flats and under the flats. Then see if you can tell how many units will be left.
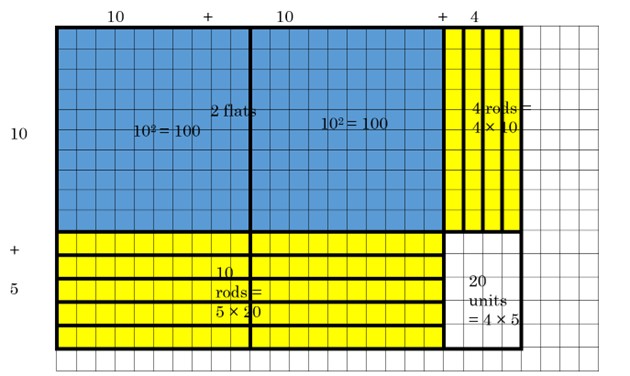
We will need 4 flats on the right, and 10 rods underneath. The units will always be what remains on the bottom right. In this example, that is where the 4 across meets the 5 going down, to give you 4 × 5 = 20 units.
1b) 24 × 15 can be written vertically:
| 20 + 4 | ||
| × 10 + 5 | ||
| 100 + 20 | The 100 is represented by the 10 rods, the 20 is the 20 units. | |
| 200 + 40 | The 200 is represented by the two flats, the 40 is the 4 rods. | |
| 200 + 140 + 20 = 360 |
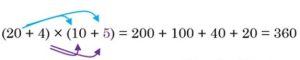
1c) The binomial multiplication ![]() is similar to the numerical multiplication 24 × 15.
is similar to the numerical multiplication 24 × 15.
| × |
||
Horizontally: ![]()
We can draw a picture showing the binomial multiplication using algebra tiles that is similar to using base ten blocks.
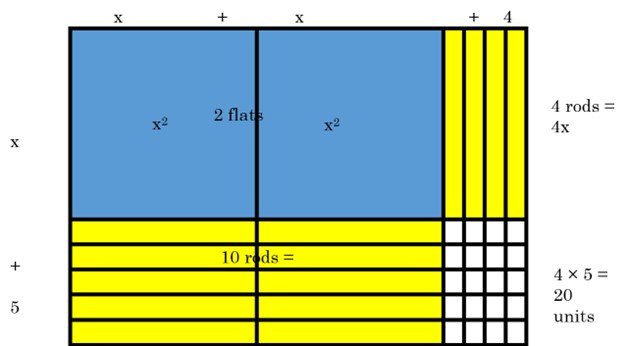
This is the same as the breakdown of flats, rods and units that we had for 24 × 15. But now, one flat is worth x2 instead of 102. Since the “flat” is in the shape of a square, it makes sense that we can represent “x squared” as a physical square. One rod is worth x, so 4x is represented by 4 rods and 10x is represented by 10 rods. Since we do not know the exact value for x, we do not make a grid.
Question: Now you try!
Example 2 Compare the partial products multiplication for 532 × 42 to the multiplication 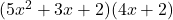 . When you are done, see what happens when you let x = 10 in the algebra problem.
. When you are done, see what happens when you let x = 10 in the algebra problem.
| 532 × 42 = 500 + 30 + 2
× 40 + 2 1,000 + 60 + 4 20,000 + 1,200 + 80 |
|
| 20,000 + 2,200 + 140 + 4 | |
| 20 cubes (thousands), 22 flats (hundreds), 14 rods (tens), 4 units (ones) | 20 cubes ( |
In both problems, when we work out the answer, we move the second row over one place value. This makes the tens line up under each other in the numerical problem and makes the like terms 10x2 and 12x2 and like terms 6x and 8x line up under each other in the algebra problem.
There is a similar structure in the answers: the same number of cubes, flats, rods and units.
If you prefer to multiply horizontally, it may be easier to place the binomial first, so you have (4x + 2)(5x2 + 3x + 2). The arrows, below, show that we multiply 4x by each term in parenthesis (4x times 5x2 , then 4x times 3x and finally 4x times 2). Next, we multiply 2 by each term in the parenthesis (2 times 5x2 , then 2 times 3x and finally 2 times 2). We get (4x + 2)(5x2 + 3x + 2) = 20x3 + 12x2 + 8x + 10x2 + 6x + 4.
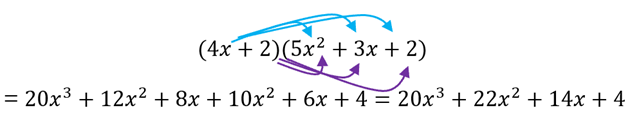
Finally, if we let x =10 in the algebra problem, then x3 =(10)3 =1000, so we get 20x3 = 20,000, the same as in the numerical version, and we get 22x2 = 22(10)2 = 2200, and so on – we get all the same values as in the first problem.
Question: Now you try!
Further Connection to Algebra: Arithmetic Sequences
Skip counting and multiples can also be used to find the next number in a pattern, and to find the algebraic formula for a pattern. For example, the pattern of multiples of 5 skips every 5: 5, 10, 15, 20, 25, 30, etc.

The pattern helps us to see that the next number is 35, since 30 + 5 = 35. Another way to understand that the next number is 35 is that we have 5 + 5 + 5 + 5 + 5 + 5 + 5. Since we have added 5 together 7 times, we could write 5 × 7, which is 35.
The algebraic formula for this sequence is y = 5n, since repeated addition of 5 means that we are multiplying by 5.
The formula may be easier to see if we number the pattern, using n to designate which number in the pattern we are on. The number that corresponds to n = 0 is our starting number. In this case, we’ll have our starting number be zero, since 0 + 5 = 5, so now we have the sequence: 0, 5, 10, 15, 20, 25, …. This sequence is still the multiples of 5, now starting at 0 × 5.
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y = | 0 | 5 | 10 | 15 | 20 | 25 | 30 | ? |
| +5 | +5 | +5 | +5 | +5 | +5 | +5 |
Thus, to find the 7th multiple of 5, we let n = 7 in the formula y = 5n. We get y = 5(7) = 35, just as before.
Example 3 How would we write a formula for the sequence 1, 6, 11, 16, 21, …. and what would the next number be?
Let’s begin by using the problem solving strategy of creating a table.
| n = | 0 | 1 | 2 | 3 | 4 | 5 | ||
| y = | 1 | 6 | 11 | 16 | 21 | ? | ||
| +? | +? | +? | +? |
What is our starting number? What number is being added on each time?
The sequence still adds 5 on each time, but this time, it starts at 1. That means that to get the 4th number, we would have 1 + 5 + 5 + 5 + 5 = 1 + 5(4) = 1 + 20 = 21. If you check the table, you can see that yes, 21 is the fourth number.
To get the equation, we use the variable, n, to stand for any number we are on. Instead of trying to get the 4th number, we are trying to get the nth number. Start at 1, add 5, add 5, add 5…. however many times we need to add 5.
This gives us the equation y = 1+5n .
To check, let’s let n = 4 in the formula: y = 1 + 5(4) = 1 + 20 = 21. Yes, it works!
The 7th number will be: y = 1+5(7) = 36 , which you can also see from the pattern of ending digits, or from adding 5 to the previous number, 31 + 5 = 36.
Example 4 Use successive differences to find the formula for the sequence 3, 7, 11, 15, 19, 23, 27, … , and find the next number.
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| y = | 3 | 7 | 11 | 15 | 19 | 23 | 27 | ? |
| +? | +? | +? | +? | +? | +? | +? |
Since the sequence starts at 3 and adds 4 each time, the equation will be y = 3+4n .
Remember that adding 4 repeatedly is the same as multiplying by 4. For example, if we start at 3 and add 4 on seven times, we have3 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 3 + 4(7).
Using the formula, the next number will be y=3+4(7) = 31, which is the same as what we would get adding 27 + 4.
Using a table or pattern to graph an equation
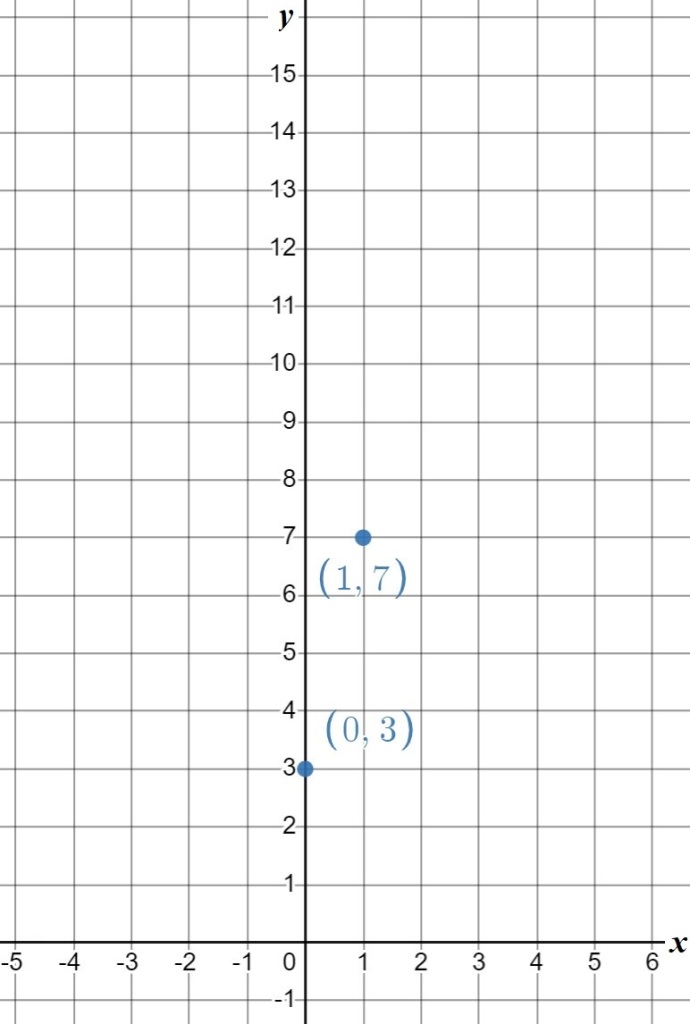
We can also write the table in example 4 as a table of values that correspond to points on the coordinate system:
| x (or n) | y | point |
| 0 | 3 | (0,3) |
| 1 | 7 | (1,7) |
| 2 | 11 | |
| 3 | 15 |
See if you can fill in the next two points in the table and then draw the points on a coordinate grid.
The first two points are drawn for you. Try filling in two more points and draw the line through the points before you scroll down.
What are the next two points on the graph? (Tip: use the table.)
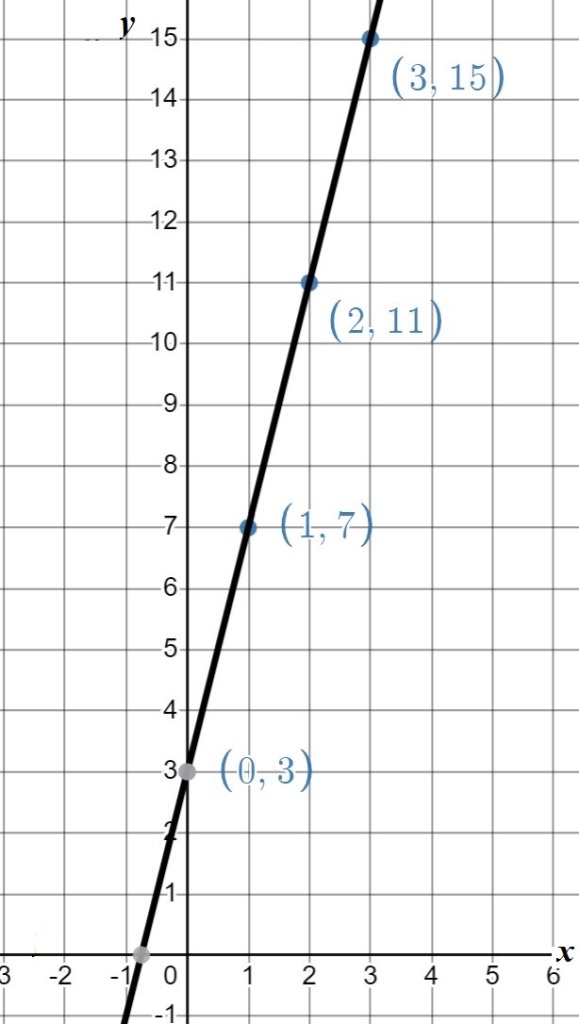
The next two points are (2,11) and (3, 15).
What is y-intercept? (Tip: this is where the line crosses the y-axis.)
The y-intercept is (0,3), where the line crosses the y-axis, which always happens when x is zero.
What is the slope? The slope is 4, the same as the number we added each time.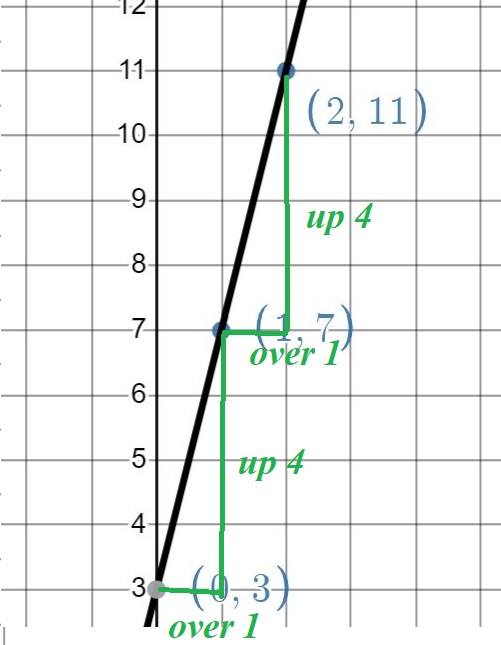
On the graph you can see the line always goes up 4 and one to the right. This is the same as saying that for every new integer (+1), we add 4 to our pattern.
You may remember the general formula for the equation of a line as y = mx + b, with m, the number in front of x, as the slope, and b as the y-intercept. Therefore, our equation is y = 3x + 4.
The equation y = 3x + 4 is the same equation that we got knowing that the sequence starts at 3 and adds 4 each time, y = 3+4n . We also could write this equation changing the order, as y = 4n + 3. In our pattern, we use the variable, n, but you can also write the formula with the variable, x.
The key take-away: if we repeatedly add the same number over and over to the output, we have a linear equation that can be represented by a straight line.
- The number that we add over and over is the slope of the line.
- We know we have a line because the slope always stays the same.
- The starting number of the sequence (when x = 0) is the y-intercept of the graph (where the line crosses the y-axis).
- To get the equation of the sequence, we can think of starting at a number and adding on to it over and over. Repeated addition is multiplication, so that’s the number we will multiply by x. The equation is y = starting number + (repeatedly added number)x.
- Or we can write the equation as y = mx + b, where m is the slope and b is the y-value of the y-intercept.
Example 5 With the sequence 8, 12, 16, 20, 24, 28 a) Rewrite this sequence as a table of points. b.) Find the starting number and how much is being added each time. c)Write the equation of the line. d)Identify the slope and y-intercept.
a. We can rewrite the sequence horizontally as
| n = | 0 | 1 | 2 | 3 |
| y = | 8 | 12 | 16 | 20 …. |
| +? | +? | +? |
or, as a table of points:
| x (or n) | y | point |
| 0 | 8 | (0,8) |
| 1 | 12 | (1,12) |
| 2 | 16 | (2,16) |
| 3 | 20 | (3,20) |
b. The starting number is 8. The number 4 is being added on each time.
c. The equation is y = 8 + 4x
d. The y-intercept is (0,8) and the slope is 4. We could also write the equation in y = mx + b form as y = 4x + 8.
Question: Now you try!
Historic Methods of Multiplication
The Lattice Method
The lattice method of multiplication has been used historically in many cultures, including in China, Europe, and Arabic cultures. The lattice method has been used for centuries. Below is an illustration from 1544, from a book of arithmetic practice by French mathematician Oronce Finé, which shows 354 multiplied by 265.

Here’s a smaller example, to show you how it works.
Example 6 Multiply 381 × 54 using the lattice method.
We’ll need 3 boxes across (for the three-digit number) and two going down (for the two-digit number). Each box has a diagonal in it.
The first box on the top left will be filled-in with the answer to 3 × 5, since this box is directly under the 3 and across from the 5: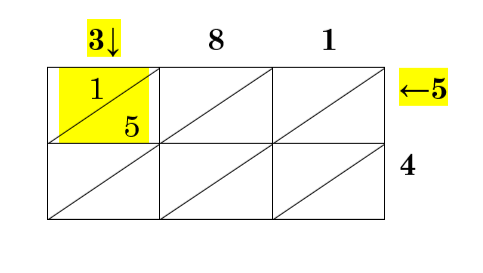
Try filling in the rest of the boxes on your own before going on.
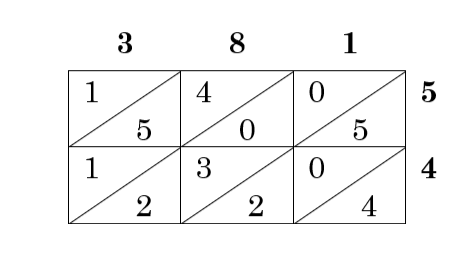
Once you have found all the individual multiplied pairs, add along the diagonals. If you get 10 or more on one diagonal, carry to the next diagonal.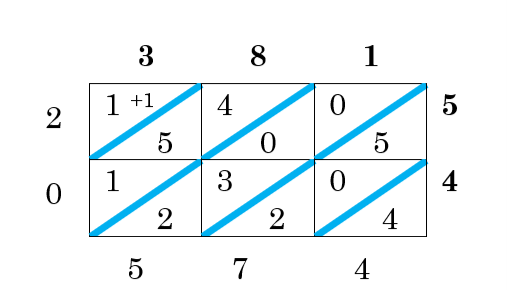
The answer is around the edges of the box! 381 × 54 = 20,574
This method, like partial products multiplication, does not require students to multiply and add at the same time, the way the standard algorithm does. It may be easier for some students because it organizes all the multiplication. On the other hand, unlike partial products multiplication, this method does not have a connection to the base ten reasoning behind it.
Question: Now you try!
Duplation and Mediation
And now for one of the strangest multiplication methods we have seen! Supposedly it’s how “Russian Peasants” did their multiplication, but there doesn’t seem to be any actual direct evidence of this1. Still, it’s super cool, because all you have to do is double the numbers, then add. No actual multiplying needed!!
Example 7 Multiply 243 × 41 using duplation (doubling) and mediation (cutting in half).
For this method, we double one side, and cut the other side in half. It does not matter which side we double and which side we cut in half. When we cut a number in half, we ignore any decimal or remainder.
| Double | Cut in half |
| 243 | 41 |
| 486 | 20 (actually, it should be 20.5, but we ignore the decimal) |
| 972 | 10 |
| 1944 | 5 |
| 3888 | 2 (again, ignore the decimal) |
| 7776 | 1 |
Next, cross out any pairs where the cut in half side is even.
| Double | Cut in half |
| 243 | 41 |
| 486 | 20 (cross out this pair because 20 is even) |
| 972 | 10 (cross out this pair because 10 is even) |
| 1944 | 5 |
| 3888 | 2 (cross out this pair because 2 is even) |
| 7776 | 1 |
Add the remaining numbers on the doubled side: 243 + 1944 + 7776 = 9963
And now check by multiplying: 243 × 41 = 9963
WOW! We just multiplied 243 × 41 only using doubling and cutting in half.
Why does this work?
To see why, first write 41 in binary (base 2):
| 25 | 24 | 23 | 22 | 21 | 20 |
| 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 |
41 = (1 × 32) + (0 × 16) + (1 × 8) + (0 × 4) + (0 × 2) + (1 × 1)
41 = 1010012
Next, line up the binary number alongside the duplation and mediation.
| Double | Cut in half | ||
| 243 | 41 | 1 | 243 × 1 |
| 486 | 20 | 0 | 243 × 0 (so it gets crossed out) |
| 972 | 10 | 0 | 243 × 0 (so it gets crossed out) |
| 1944 | 5 | 1 | 243 × 8 |
| 3888 | 2 | 0 | 243 × 0 (so it gets crossed out) |
| 7776 | 1 | 1 | 243 × 32 |
Add up the numbers that are not crossed out, and you are adding (243 × 1) + (243 × 8) (doubled 3 times, 8 = 23) + (243 × 32) (doubled 5 times, 32 = 25). Duplation and Mediation is like multiplying by the number in binary!
This method is probably not one you would use to teach elementary school children, since it is fairly complicated. We present it here because of the connection it has to binary (base 2) and because it is so interesting so see a multiplication method that requires only doubling and cutting in half, with no times tables to memorize!
Scaffold Division (optional topic)
With Scaffold division, students use easy numbers to approximate how much will divide in to a number.
The key difference between scaffold division and our “regular” long division is that a student can pick any number, instead of having to try to find the largest possible number of times that the number divides in.
Example 8 Divide 210 ÷ 6 using scaffold division.
Normally, we might ask if 6 goes into 21, just the first two digits of the three-digit number. For students first learning how to divide larger numbers, it can be very confusing to only be looking at two of the place values.With scaffold division, a student can instead ask themselves multiplication questions, to get as close to 210 as possible. For example, a student might start off with 10 × 6 = 60, since that’s easy to do:
Students will learn to do this division more quickly by combining numbers. For example: Scaffold division can also work well with much larger numbers, and even if there is a remainder.
Scaffold division can also work well with much larger numbers, and even if there is a remainder.
Example 8 Divide 3,529 ÷ 14 using scaffold division Certainly, this division method takes longer than our usual method, but as students see how it works, they may want to start combining numbers more quickly, which can then lead to the standard division method.
Certainly, this division method takes longer than our usual method, but as students see how it works, they may want to start combining numbers more quickly, which can then lead to the standard division method.
Partial products, the lattice method of multiplication and the scaffold method of division can be great ways to teach children, but they have the drawback that they may confuse parents, who may get upset that they don’t understand this strange “new” way their child is using to multiply or divide (actually, the lattice method is a very old method). In schools that use alternate methods like these, it is important to educate the parents as to what is being taught and why. Many schools hold workshops for parents so that they can see how their child is learning math. Parents need to know that it is important for them not to wreck the gradual path their child is taking by showing them a “faster” or “easier” way before the child is ready.
Some parents are convinced that the new strategies for multiplying and dividing mean that their children are learning an inferior kind of math. In this news story from 2014, http://wqad.com/2014/02/03/same-math-new-method-can-you-and-your-child-keep-up/, a woman pulls both of her boys out of school and decides to home school them, because she cannot understand their homework and so cannot help them with it. In The Eagle Forum, https://eagleforum.org/publications/column/exposing-the-common-core-fraud.html, conservative commentator Phyllis Shlafley argues that students would be much better off memorizing than using the new “common core math.” She writes, “Common Core math is based on the theory that students are expected to discover math principles for themselves, instead of memorizing time-tested math shortcuts that almost everyone can easily learn.” Her comment ignores the fact that it is often very hard to remember procedures and short cuts that don’t make sense, as many of us can attest!
sec-2.2-homeworkDownloadsec-2.2-homework-answersDownload
Unless otherwise specified, images in this section are by Kathleen Offenholley and licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.