A 3.1: Using Sets to Find Common Factors; Fraction Review

Kathleen Offenholley; Fatima Prioleau

A 3.1: Using Sets to Find Common Factors; Fraction Review

Chapter 3 Section A1

Algebra Topics – Common factors for Algebraic Expressions; Using Common Factors to Simplify, Add and Subtract Algebraic Fractions

Common Factors

In the previous section, we saw how sets could be used to find common factors. For example, to find the common factors of 24 and 40, we can list all the factors of both numbers, and see in a list what factors they both have in common.

The factors of 24: {1, 2, 3, 4, 6, 8, 12, 24}

The factors of 40: {1, 2, 4, 5, 8, 10, 20, 40}

We can see that both lists have the numbers 1, 2, 4, 8 in common. As we saw in the previous section, a Venn diagram can be a way to see this visually:

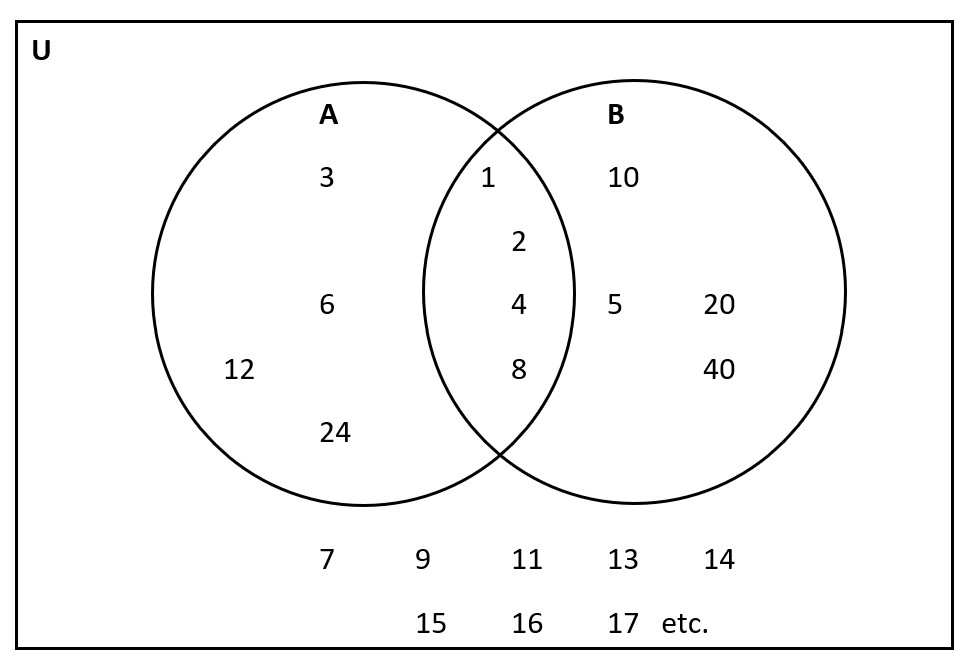
The numbers in the intersection are the factors of both 24 and 40.

A ∩ B = {1, 2, 4, 8}

The largest number in this set is 8. Thus, the greatest common factor of 24 and 40 is 8. We saw that this could be used to reduce $\frac{24}{40}=\frac{24 \div 8}{40 \div 8}=\frac{3}{5}$ .

We can also find common factors for algebraic expressions.

Example 1 Find some of the factors of $8x^3y$

Finding the factors is the same as finding the numbers and variables that divide into $8x^3y$ . We know the expression $8x^3y$ is divisible by 2. It can be helpful to list what we get when we do divide by 2, since that result is also a factor. $8x^3y\div 2 = 4x^3y$ , so this gives us two factors, 2 and $4x^3y$ .

We also know that x is a factor because $8x^3y$ is the same as $8\cdot x\cdot x \cdot x \cdot y$ . If we divide $8x^3y$ by x we get $8x^2y$ . Notice that the exponent goes down by 1 when we divide — we subtract 1. And when we multiply, we add 1: $x \cdot 8x^2y = 8x^3y$ .

See if you can complete the list of pairs factors of $8x^3y$ by filling in the blank parts on the right side.

1

$8x^3y$

2

$4x^3y$

4

$2x^3y$

8

$x$

$8x^2y$

$x^2$

$x^3$

$y$

Note that this table does not contain all the possible combinations of factors of $8x^3y$ — instead, it’s helping us get a feel for what some of the factors are.

Example 2 Find the common factors for $8x^3y$ and $20x^2y^4$ , then find the largest common factor.

To find the common factors, list the numbers — and variables — that both are divisible by. For example, we know that both $8x^3y$ and $20x^2y^4$ are divisible by 2. Is there a larger number that goes into both? We know that both are divisible by x. Is there a larger power of x that both are divisible by? And finally, what is the largest power of y that divides into both? If it helps, you can think of yourself as trying to complete the Venn diagram of the factors of the two expressions:

This Venn diagram is not complete, since it would be difficult to list all the possible combinations of factors, but it does give an idea of how you can sort through the factors in your mind, even if you don’t draw the diagram. The greatest common factor for the two expressions is $4x^2y$ , since 4 is the largest number that divides into both, $x^2$ is the largest power of x that divides into both, and y (or $y^1$ ) is the largest power of y that divides into both.

Example 3 Use the factors in example 2 to simplify the fraction $\frac{8x^3y}{20x^2y^4}$ .

We can simplify gradually, using some of the factors we know, such as 2: $\frac{(8x^3y) \div 2}{(20x^2y^4) \div 2} = \frac{4x^3y}{10x^2y^4}$ , then 2 again: $\frac{(4x^3y) \div 2}{(10x^2y^4) \div 2} = \frac{2x^3y}{5x^2y^4}$ , then x: $\frac{(2x^3y) \div x}{(5x^2y^4) \div x} = \frac{(2x^2y)}{(5xy^4)}$ , then x again: $\frac{(2x^2y) \div x}{(5xy^4) \div x} = \frac{2xy}{5y^4}$ , and finally y: $\frac{(2xy) \div y}{(5y^4) \div y} = \frac{2x}{5y^3}$

Or, since we know that the largest common factor is $4x^2y$ , we can divide by that to simplify the fraction in one step. $\frac{(8x^3y) \div (4x^2y)}{(20x^2y^4) \div (4x^2y)} = \frac{2x}{5y^3}$ .

We can also return to earlier methods of expanding out the multiplication and cancelling: $\frac{8x^3y}{20x^2y^4} = \frac{2 \cdot 2 \cdot 2 \cdot x\cdot x \cdot x \cdot y}{2 \cdot 2 \cdot 5 \cdot x \cdot x \cdot y \cdot y \cdot y \cdot y}$ =

= $\frac{2x}{5y^3}$ .

The best method is the one that works best for you to both understand what you are doing and be able to get the correct answer. The best method for you may not always be the fastest method. Fast is not always better.

Adding and Subtracting Fractions Using Factors

Recall that to add two fractions, they must have a common denominator, and then we add or subtract the numerators and keep that common denominator. For example, $\frac{3}{5x} + \frac{y}{5x} = \frac{3+y}{5x}$ , and similarly for subtraction, $\frac{3}{5x} - \frac{y}{5x} = \frac{3-y}{5x}$

If the two fractions do not have a common denominator, one of the quickest ways to get a common denominator is to multiply the first fraction by the second denominator, top and bottom, and vice versa. For example if we have, $\frac{3}{5x} + \frac{x}{3y}$ , we can multiply the first fraction by $\frac{3y}{3y}$ and the second by $\frac{5x}{5x}$ . This is allowed because both these two fractions are equal to 1, so multiplying by 1 will give us two new fractions that are equivalent to the old ones. We get:

$\frac{3 \cdot (3y)}{5x \cdot (3y)} + \frac{x \cdot (5x)}{3y \cdot (5x)} = \frac{9y}{15xy} + \frac{5x^2}{15xy} = \frac{9y + 5x^2}{15xy}$

Sometimes, using this method can result in a large common denominator and you will have to simplify the fraction in the end.

For example, if we have, $\frac{5}{2xy} + \frac{x}{4y}$ , we can multiply the first fraction by $\frac{4y}{4y}$ and the second by $\frac{2xy}{2xy}$ .

We get: $\frac{5 \cdot (4y)}{2xy \cdot (4y)} + \frac{x \cdot (2xy)}{4y \cdot (2xy)} = \frac{20y}{8xy^2} + \frac{2x^2y}{8xy^2} = \frac{20y + 2x^2y}{8xy^2}$ .

The numerator and denominator of our answer have factors in common — all the terms are divisible by 2 and by y. We can simplify either by dividing every term by 2y, or factoring out 2y: $\frac {20y \div (2y)+ 2x^2y \div (2y)}{8xy^2 \div (2y)} = \frac{10 + x^2}{4xy}$ .

The reason we ended up having to simplify is that our original denominators had some factors in common. When that is the case, there is another way to get a smaller common denominator: multiply the first fraction by the factors that second denominator has, but the first denominator does not, and vice versa.

For example, with the fractions $\frac{5}{2xy} + \frac{x}{4y}$ , both fractions already have a factor of 2, and both already have the variable, y. The first fraction’s denominator needs another factor of 2 in it, so that it becomes 4xy. The second fraction’s denominator needs an x, so that it becomes 4xy as well. Thus, we can multiply the first fraction by 2/2 and the second fraction by x/x:

We get: $\frac{5 \cdot (2)}{2xy \cdot (2)} + \frac{x \cdot (x)}{4y \cdot (x)} = \frac{10}{4xy} + \frac{x^2}{4xy} = \frac{10 + x^2}{4xy}$ .

Example 4 Add the fractions $\frac{7}{8x^3y}+\frac{z}{20x^2y^4}$ using the smallest common denominator.

Notice that the two denominators here are the same as the ones we found factors for in example 1. To multiply the first fraction by what it is missing that the other denominator has, you might think again of our Venn Diagram. But this time, instead of looking at the intersection — the overlap between the two circles, think of the outside of the first circle, what factors $8x^3y$ does not have. It does not have a factor of 5, and it does not have a power of y that goes up as high as y⁴.

If we multiply that first fraction by $\frac{5y^3}{5y^3}$ , that will give that first fraction the factor of 5 that it is missing and will get the power of y up to 4. $\frac{7 \cdot 5y^3}{8x^3y\cdot 5y^3} = \frac{35y^3}{40x^3y^4}$

What is missing in the denominator of the second fraction? Tip: now look at what is outside of the second circle. We can see that 8 is outside the second circle, and we also see that outside the circle, the highest power of x is the third power. What can we multiply $20x^2y^4$ by to make the power of x go up and to make there be a factor of 8 in the coefficient?

Caution: we do not need to multiply by $8x^3$ . 20 already has a factor of 4 in it (4 x 5 = 20), and it already has $x^2$ .

We need to multiply by $2x$ : $\frac{z \cdot 2x}{20x^2y^4\cdot 2x} = \frac{2xz}{40x^3y^4}$

Now we have the same denominator for both fractions, and we can add: $\frac{35y^3}{40x^3y^4}+\frac{2xz}{40x^3y^4}= \frac{35y^3 + 2xz}{40x^3y^4}$

If the Venn diagram was not helpful to you, think of another strategy, like creating a table. First, breakdown all the factors of each denominator. Then, place the factors into a table. Break the numbers and variables down completely ( $8 = 2 \cdot 2 \cdot 2$ )

$8x^3y$

2

x

y

$20x^2y^4$

2

5

x

y

Now redraw the table, leaving empty spaces where one of the denominators does not have that factor. You will probably need some more columns.

$8x^3y$

2

need another 5

x

need another y

y

need another y

$20x^2y^4$

2

need another 2

5

x

need another x

y

This way we can see that the first denominator needs $5 \cdot y \cdot y \cdot y = 5y^3$ and the second needs $2 \cdot x = 2x$

Example 5 Add or subtract using the smallest common denominator:

a. 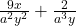$\frac{9x}{a^2y^2} + \frac{2}{a^3y}$

b. 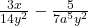$\frac{3x}{14y^2} - \frac{5}{7a^5y^2}$

Again, we will multiplying by the factors that each denominator is missing, instead of by the whole other denominator:

a. $\frac{9x}{a^2y^2} + \frac{2}{a^3y}$

The first fraction has a² in the denominator, while the second one has a³. That means the first fraction needs another factor of a.

The second fraction has y in the denominator, while the first has y². That means the second fraction needs another factor of y.

$\frac{9x}{a^2y^2} + \frac{2}{a^3y} = \frac{9x \cdot a}{a^2y^2 \times a} + \frac{2 \cdot y}{a^3y \cdot y} = \frac{9xa}{a^3y^2} + \frac{2y}{a^3y^2} = \frac{9xa + 2y}{a^3y^2}$

b. $\frac{3x}{14y^2} - \frac{5}{7a^5y^2}$

The first fraction has y ² in the denominator, like the second fraction, but it doesn’t have a⁵. That means the first fraction needs a⁵.

The first fraction has 14 = 2 × 7 in the denominator, while the second one has 7. That means the second fraction needs a factor of 2.

$\frac{3x}{14y^2} - \frac{5}{7a^5y^2} = \frac{3x \times a^5}{14y^2 \times a^5} - \frac{5 \times 2}{7a^5y^2 \times 2} = \frac{3a^5x}{14a^5y^2} - \frac{10}{14a^5y^2} = \frac{3a^5x - 10}{14a^5y^2}$

Question: Now you try! Several simple mult. choice with simple adding and simplifying that can be reduced or added only with what’s missing

A 3.1: Using Sets to Find Common Factors; Fraction Review

Chapter 3 Section A1

Common Factors

Example 1 Find some of the factors of $8x^3y$

Example 2 Find the common factors for $8x^3y$ and $20x^2y^4$ , then find the largest common factor.

Example 3 Use the factors in example 2 to simplify the fraction $\frac{8x^3y}{20x^2y^4}$ .

Adding and Subtracting Fractions Using Factors

Example 4 Add the fractions $\frac{7}{8x^3y}+\frac{z}{20x^2y^4}$ using the smallest common denominator.

Example 5 Add or subtract using the smallest common denominator:

a. $\frac{9x}{a^2y^2} + \frac{2}{a^3y}$

b. $\frac{3x}{14y^2} - \frac{5}{7a^5y^2}$

License

Share This Book

Chapter 3 Section A1

Common Factors

Example 1 Find some of the factors of

Example 2 Find the common factors for and , then find the largest common factor.

Example 3 Use the factors in example 2 to simplify the fraction .

Adding and Subtracting Fractions Using Factors

Example 4 Add the fractions using the smallest common denominator.

Example 5 Add or subtract using the smallest common denominator:

a.

b.

License

Share This Book

Example 1 Find some of the factors of $8x^3y$

Example 2 Find the common factors for $8x^3y$ and $20x^2y^4$ , then find the largest common factor.

Example 3 Use the factors in example 2 to simplify the fraction $\frac{8x^3y}{20x^2y^4}$ .

Example 4 Add the fractions $\frac{7}{8x^3y}+\frac{z}{20x^2y^4}$ using the smallest common denominator.

a. $\frac{9x}{a^2y^2} + \frac{2}{a^3y}$

b. $\frac{3x}{14y^2} - \frac{5}{7a^5y^2}$