A 2.2 Algebra Extension: Operations on Polynomials – Adding, Subtracting, Multiplying and Factoring
Chapter 2 Section A2
Algebra Topics – What is a Polynomial? Adding, Subtracting, Multiplying and Factoring
Elementary Education – Distributive Property
What is a Polynomial?
A polynomial is an expression composed of variables with exponents, and constant terms, involving addition, subtraction and multiplication of the variables.
A polynomial may have some or all of these features:
Constants –for example: , -4, 6
Variables –for example: x, mn, y
Exponents –for example: ![]()
There are three different types of polynomials, based on the amount of terms the polynomial contains. Terms are the added (or subtracted) parts.
A monomial is a polynomial with one term (mono means one), such as 5x, or 2y3.

Similarly, a monocle has one eyepiece.
A binomial is a polynomial with two terms (bi means two), such as 4y3 + 3x2, or ![]()

Similarly, a bicycle has two wheels.
A trinomial is a polynomial with three terms (tri means three), such as ![]() .
.
A trilogy has three episodes (and a tricycle has three wheels).
If the polynomial has more than three terms, we just call it a polynomial. Poly means many.
In a previous section, we looked how adding polynomials is similar to adding in base ten. For example, to add the two trinomials such as ![]() and
and ![]() , we could line up “like terms” – terms that have the same variable and exponent – the same way we line up the place values in base ten:
, we could line up “like terms” – terms that have the same variable and exponent – the same way we line up the place values in base ten:
|
______________
|
________
|
_______________
|
The base ten place values are similar to our “like terms” because the base ten place values have the same exponents. The similarity breaks down somewhat when we go into negative numbers and subtraction, but we are still combining like terms. In this section, we’ll look at more complicated like terms.
Combining More Complicated Like Terms when Adding and Subtracting
Like terms have the same variables or variable expression, to the same exponents. For example, ![]() and
and ![]() are like terms. Both have the same variable, x, and the same exponent of 2. We can add
are like terms. Both have the same variable, x, and the same exponent of 2. We can add ![]() . Similarly,
. Similarly, ![]() and
and ![]() are also like terms, with the same variables and exponents, so we can add
are also like terms, with the same variables and exponents, so we can add ![]()
On the other hand, ![]() and
and ![]() are not like terms, so we cannot add the 5 and the 4 – that would be like adding 5000 + 400 to get 9000.
are not like terms, so we cannot add the 5 and the 4 – that would be like adding 5000 + 400 to get 9000.
Example 1 Match the expressions that are like terms and can be added, then add them together. Caution: not all of them will match up!
| 1. |
a. |
| 2. |
b. |
| 3. |
c. |
| 4. |
d. |
| 5. |
e. |
1. We can add like terms ![]() , and
, and ![]() . We get
. We get ![]() .
.
2. We can add like terms, ![]() and
and ![]() . We get
. We get ![]() .
.
3. We can add like terms, ![]() and
and ![]() . We get
. We get ![]() .
.
4. We can add like terms ![]() , and
, and ![]() . We get
. We get ![]() .
.
5. None of the choices are like terms with ![]() .
.
Example 2 Match the expressions that are like terms and then subtract them. Caution: not all of them will match up!
| 1. |
a. |
| 2. |
b. |
| 3. |
c. |
| 4. |
d. e. |
1. ![]() and
and ![]() are like terms and can be subtracted. We get:
are like terms and can be subtracted. We get: ![]() .
.
2. None of the choices are like terms with ![]() .
.
3. ![]() and
and ![]() are like terms and can be subtracted. We get:
are like terms and can be subtracted. We get: ![]() .
.
4. ![]() and
and ![]() are like terms and can be subtracted. We get:
are like terms and can be subtracted. We get: ![]() . Remember that subtracting a negative is the same as adding because we are taking away the subtraction. You can also think of subtracting a negative as the opposite of subtracting, which is addition. In terms of money, if I’m $5 in debt, if someone takes away that $5 debt, I have $5 more than before. – (–$5) = +$5
. Remember that subtracting a negative is the same as adding because we are taking away the subtraction. You can also think of subtracting a negative as the opposite of subtracting, which is addition. In terms of money, if I’m $5 in debt, if someone takes away that $5 debt, I have $5 more than before. – (–$5) = +$5
Multiplying Using the Distributive Property
The distributive property of multiplication over addition states that multiplying the sum of two or more numbers is the same as multiplying the addends separately.
For example, when multiplying 3 × 9, you can break 9 up into 4 + 5, and you can multiply
3 × 9
= 3 × (4 + 5)
= (3 × 4) + (3 × 5)
= 12 + 15 = 27, the same as what you get multiplying 3 × 9. This might be a way to multiply if you don’t yet know your 9’s times tables, but it would probably be easier instead to add 9 + 9 + 9. There are many ways to correctly work out a problem!
Where the distributive property of multiplication over addition is really useful, as we saw in Section 2.2, is when we multiply two- and three-digit numbers. For example, multiplying a polynomial by a monomial is similar to what we already know how to do when we multiply a several digit number by a single digit number:
| 234
× 2 |
_____________________ |
| 468 |
In the first problem, we multiply each digit by 2. In the second, we multiply each term by 2x. Notice how each power of the exponent increases by one, since when we multiply, we add the exponents.
We often write this second problem as ![]() and think of the term on the outside of the parentheses as being multiplied by each term on the inside.
and think of the term on the outside of the parentheses as being multiplied by each term on the inside.
Example 3 Multiply 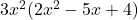 by stacking the polynomial on top, the monomial under it, and using the distributive property. Then do the same problem by working the problem side-by-side and using the distributive property.
by stacking the polynomial on top, the monomial under it, and using the distributive property. Then do the same problem by working the problem side-by-side and using the distributive property.
_______________
|
Or, we multiply ![]() by first multiplying
by first multiplying ![]() , then
, then ![]() , and finally,
, and finally, ![]() , and we get
, and we get ![]() .
.
Example 4 Multiply the two binomials: 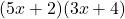
Multiplying the two binomials ![]() can be done in a similar way to multiplying 52 × 34
can be done in a similar way to multiplying 52 × 34
| 52
× 34
|
50 + 2 × 30 + 4 200 + 8 1500 + 60 1500 + 260 + 8 = 1,768 |
_________________________
__________________________
|
|
|
|
Notice how the place values increase as we multiply our base ten numbers, in much the same way our variable increases in power when we multiply the binomials.
Patterns in Binomial Multiplication
Interesting patterns emerge when we multiply binomials. Use the examples below, to see if you can see a pattern that relates the numbers we multiply, and the middle and last terms in our answers.
![]() How do the 2 and 3 relate to the middle term,
How do the 2 and 3 relate to the middle term, ![]() , and the end number, 6?
, and the end number, 6?
![]() How do the 1 and 7 relate to the middle term,
How do the 1 and 7 relate to the middle term, ![]() , and the end number, 7?
, and the end number, 7?
![]() How do the 5 and 2 relate to the middle term,
How do the 5 and 2 relate to the middle term, ![]() , and the end number, 10?
, and the end number, 10?
One you see the pattern, try to predict the answer to ![]() , and then multiply it out to see if you are correct.
, and then multiply it out to see if you are correct.
The pattern is that the end terms in each binomial add together to get the middle term in the trinomial answer, and multiply together to get the end term.
The reason for this pattern is clear when we stack the terms to add them:
_____________________ |
|
____________________ |
In this line, we see where we multiply 7 × 2 = 14
|
| In this line, we see where we add |
Example 5 Predict the two binomials that were multiplied to get 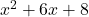 .
.
From the pattern, we know that the constants in the binomials will have to multiply to get 8 and add to get 6. We know that 1 × 8 = 8, but also that 2 × 4 = 8. The first pair 1 and 8, add up to 9. The second pair, 2 and 4, add up to 6. Thus we have ![]()
When we use the pattern to try to figure out the two binomials, this is known as factoring the trinomial. We are finding the two factors that multiply to get that particular trinomial.
Example 6 Factor each of these trinomials into two binomials: a. 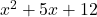 b.
b. 
Both trinomials end in 12, so we are looking for two numbers that multiply to get 12. In part a, ![]() , we are looking for two numbers that multiply to get 12 and add to get 5. In part b,
, we are looking for two numbers that multiply to get 12 and add to get 5. In part b, ![]() , we are looking for two numbers that multiply to get 12 and add to get 8.
, we are looking for two numbers that multiply to get 12 and add to get 8.
We get a) ![]() and b)
and b)![]()
Thus far, we have focused on trinomials that have only positive terms. What happens when we multiply binomials with negative constants, such as ![]() ?
?
Example 7 Multiply 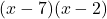 and predict what kinds of trinomials we will get when the two constants are negative.
and predict what kinds of trinomials we will get when the two constants are negative.
_____________________ |
|
____________________ |
Note that a negative times a negative is a positive, so -7 × -2 = 14
|
| In this line, we add |
Thus, if we have a trinomial with a first term of ![]() , positive middle terms and a negative third term, we know we have two binomials with negative constants.
, positive middle terms and a negative third term, we know we have two binomials with negative constants.
Unless otherwise specified, images in this section are by Kathleen Offenholley and licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.