Chapter 2 Section A3

Algebra Topics – Solving Equations, Literal Equations; Finding Solution Sets

Elementary Education – Problem-Solving Strategies: Guess and Check, Working Backwards

Problem-Solving Strategies for Equations

Example 1 “I’m thinking of a number. If I multiply my number by 7, then add 4, I get 60. What’s my number?”

Try either the guess-and-check or working backwards strategies (no algebra!) to see if you can find the answer. Remember that it’s okay to change strategies if you find that one strategy isn’t working well for you.

For guess and check, you might start with the number 2, and see if that works. If you get a result that’s too low (lower than 60), then what do you want to do with the next guess, make it larger or smaller? Remember that children need to be taught this method of making the next guess larger or smaller based on their result, otherwise they will just guess wildly.

If you are working backwards, you should start with the number 60, and do the opposite of each operation before that.

Try both methods out before you page down!

[spoiler space]

Once you think you have the correct answer, check it in the words of the puzzle to see if you are right. You will also see the answer, below, when we work out the same puzzle using algebra.

Example 2 Solve the puzzle in example 1 using algebra.

Start by translating each part:

I’m thinking of a number. → use a variable such as x in place of the number.

If I multiply my number by 7 → 7x

then add 4 → 7x + 4

I get 60 → 7x + 4 = 60.

To solve this equation, use the same steps you used when you were working backwards.

Working backwards, you would start with the number 60, and do the opposite of each operation before that. Begin by doing the opposite of adding 4: subtract 4.

Now do the opposite of multiplying by 7: divide by 7.

This is the same answer you should have gotten with guess and check and with working backwards.

Notice that in each step, you did the opposite of what was being done to the variable, in the opposite order (working backwards).

To solve an equation algebraically

• Undo each operation that is being done to the variable by doing the opposite operation to both sides of the equation.
• Go in the opposite of the order of operations
  • undo anything adding or subtracting our variable term first
  • then undo anything that is multiplying or dividing the variable term
  • undo any exponents on our variable.
  • finally, if there are parenthesis, solve what’s inside the parenthesis.

Example 3 Solve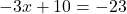 

The 10 is being added to our variable term, so subtract 10 from both sides of the equation:

Now the -3 is multiplying the variable, x, so divide both sides of the equation by -3.

Notice that we do not add 3 because the opposite of multiplying by -3 is dividing by -3, not adding.

Our solution, x = 11, is the number that will work in the original equation to make that equation true. When we substitute 11 in for x, we get , which is true since

We can use the same method to solve literal equations, that is equations where variables represent some of the values.

Example 4 Solve 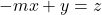for .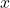

Since we are asked to solve for x, we are going to get the variable x alone on one side of the equation. We begin by undoing anything adding or subtracting to the term that has the variable, x. Notice that these steps are very similar to the ones in example 3.

The y is being added to our variable term, so subtract y from both sides of the equation:

Notice that unlike with numbers, we can’t combine the variable z with the variable y. So we just write down that they are being subtracted.

Now the -m is multiplying the variable, x, so divide both sides of the equation by -m.

Notice that the whole right side of the equation is divided by the -m.

Another way to write this is 

Example 5 Solve 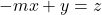for .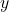

The first step here is a little trickier. Now we want to undo anything that is happening to the variable, . So in our first step, we look for whatever is being added or subtracted to the variable . The whole term, is being added to . So we need to subtract . Remember what happens when you subtract a negative? It might help to see it written down:

Subtracting is the same as adding , so we can rewrite this as

Another way to look at this is that we add mx because “cancels out” , because when you add them together, you get zero.

What is a solution to an equation?

The solution to any equation can be one number, it can be variables, as we have seen above, and it can even be a set of numbers. The solution to an equation is whatever numbers (or variables) will work to make the equation true. For example, in example 3, we saw that x = 11 is the value for x that makes the equation true, so 11 is the solution to that equation.

Example 6 Solve 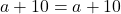and .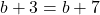

For each of these equations, let’s focus first on what works to make the equation true. In the first equation, does a = 1 work as a solution? What about a = 2? a = 3? Do the same for the second equation, and see what works in place of the variable, b: does b = 1 work as a solution? What about b = 2? b = 3?

You should quickly see in the first equation, that any number will make true, while in the second equation, no numbers work. You should also be able to see logically that a number + 10 will always equal that same number + 10; while a number + 3 will never equal that same number + 7.

We say that the solution to is all real numbers, while for , there is no solution.

What happens if you try to solve an equation like or ?

You might stop here, realizing this is a statement that is always true, not matter what value you have for a. Or you might continue by subtracting a from both sides of the equation:

0 = 0

This is a statement that is also always true. It might be a little harder from here to come to the conclusion that this means that your variable, a, can equal any number, since the variable has disappeared. But it is indeed still the case that that no matter what a is equal to, 0 = 0 will be true.

For the second equation,

You might stop here, realizing this is a statement that is never true, not matter what value you have for b. Or you might continue by subtracting b from both sides of the equation:

0 = 4

This statement is never true! This is another way to see that there is no solution to our equation.

Solving for a variable, part 1: https://www.youtube.com/watch?v=DorYar-GjC0

Solving for a variable, part 2: https://www.youtube.com/watch?v=BUVJlJXfuFo

Unless otherwise specified, images in this section are by Kathleen Offenholley and licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.