A 2.4 Algebra Extension: The meaning of Slope; Parallel Versus Intersecting Lines; Systems of Equations
Chapter 2 Section A4
Algebra Topics – What is the Slope of a Line? Parallel Versus Intersecting Lines; Systems of Equations
Elementary Education – More on Block Patterns
What is the Slope of a Line?
In a previous section, we saw that the slope of a line was the same as the number that was repeatedly added, since repeated addition means to multiply. For example, in the pattern 3, 13, 23, 33, 43…., we start at 3 and add on 10 over and over again, so we have the equation y = 3 + 10x. Thus we have the equation of a line with y-intercept 3 and slope of 10.
In this section, we’ll look more at what the slope tells us in terms of the rate of growth, and how to tell when two equations will have the same solution — where the lines intersect.
To illustrate the slope of a line, let’s look at two different students who have made patterns using blocks drawn on paper.
Example 1 Saul and Gabi’s* block patterns are below. Find the equation for each pattern and predict the next number of blocks
(*These two students are named after the two main characters in Carlos Hernandez’s amazing novel, Saul and Gabi Break the Universe.)
Saul made the following block pattern:
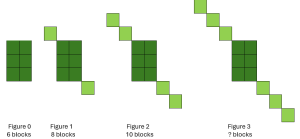
We can see that the pattern starts with 6 blocks and keeps adding 2 blocks for each new figure, so the equation for the number of blocks is y = 6 + 2x. The next pattern will have 12 blocks, which we can find by letting x = 3 in the formula: y = 6 +2(3) = 6+6 = 12, or by adding 2 to the previous number of blocks.
Gabi made the following pattern:
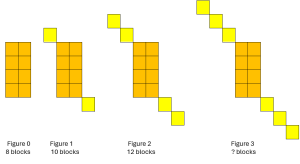
Her pattern starts with 8 blocks and adds 2 for each new figure, so the equation for the number of blocks is y = 8 + 2x. The number of blocks in figure 3 is y = 8 + 2(3) = 14, or get 14 by adding two more to figure 2.
Both Saul and Gabi have block patterns that grow by the same amount each time — each adds 2. This means that both students’ equations have the same slope of 2. We could also write their equations as y = 2x + 6 and y = 2x + 8, showing the slope first. This way to write the equation is the classic form, y= mx + b, where m stands for the slope and b stands for the y-intercept, where the graph crosses the y-axis (the starting number for these block patterns).
If we graph these equations, we have another way to see how fast they are growing. Let x = 0, then 1, then 2, etc., to make a table of points. For example, for the equation y = 2x + 6, let x = 0 and we get y = 2(0) + 6 = 0 + 6 = 6. This gives us the point (0,6). Let x = 1 and we get y = 2(1) + 6 = 2 + 6 = 8. This gives us the point (1,8). Another way to say this is that figure 1 has 8 blocks. See if you can find the point when x = 2.
Saul’s block pattern
| x | y |
| 0 | 6 |
| 1 | 8 |
| 2 | 10 |
From the table, we can also see that the y value is always adding 2, which matches the “growth” rate shown by the equation and the block patterns.
Make a similar table for the second equation, then graph both lines.
Gabi’s block pattern
| x | y |
| 0 | ? |
| 1 | ? |
| 2 | ? |
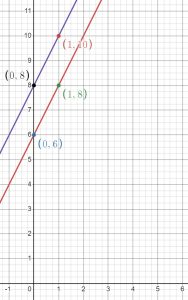
What do you notice about the two lines? The two lines are parallel.
Key take-aways:
- The slope of a line tells us how fast the line is growing.
- Two lines that have the same slope are growing at the same rate.
- Two lines that have the same slope are parallel and will never intersect each other.
Saul and Gabi will never have the same number of blocks on the same turn, because Gabi starts out with more blocks and the two towers are growing at the same rate.
Example 2 Suppose we have a new equation for a block pattern for another student, Yuko, y = 4x + 2. Is Yuko’s equation growing faster or slower than Saul’s? When will the two students have the same number of blocks on the same turn?
Note: When we have two or more equations, and we are trying to find out when they will be equal to each other, this is called finding the solution to a system of equations.
Recall that Saul’s equation was y = 2x + 6, with a slope of 2. Yuko’s equation, y = 4x + 2, has a slope of 4. Since 4 is larger than 2, the new equation is growing faster. It is adding 4 blocks per turn instead of 2.
If we make a table of points for Yuko’s equation, we can see that it has the same number of blocks as Saul’s on turn two.
Yuko’s block pattern
| x | y |
| 0 | 2 |
| 1 | 6 |
| 2 | 10 |
Saul’s block pattern
| x | y |
| 0 | 6 |
| 1 | 8 |
| 2 | 10 |
We can also see that the two lines cross at (2,10).
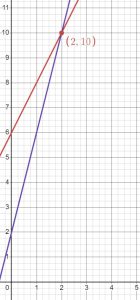
The solution to the system of equations is (2, 10). The two students will have the same number of blocks, 10, on turn 2.
Another way to find where the two equations have the same number of blocks is to notice that since the number of blocks is y, this is where the y values will be the same.
We have the equations, y = 4x + 2 and y = 2x + 6. When will the y values be equal?
The two will be equal when y = y, in other words, when 4x + 2 = 2x + 6.
We can solve that equation:
4x + 2 = 2x + 6
-2x -2x
2x + 2 = 6
-2 -2
2x = 4
/2 /2
x = 2
Once we have the x value, we can then use either equation to find y:
y = 4x + 2 = 4(2) + 2 = 8 +2 = 10
or y = 2x + 6 = 2(2) + 6 = 4 + 6 =10
Example 3 Find the pattern for the block towers below and find the slope and the equation. Graph the line, then find the number of blocks in figure 3.
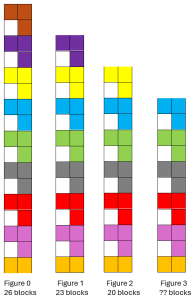
We start with 26 blocks, and then three blocks are being taken away each time. The pattern is decreasing. For example, for figure 2, we started at 26 blocks, then subtracted 3 twice. Figure 2 = 26 – 3 – 3 = 26 -3(2). The slope is negative. The equation is y = 26 – 3x, or written in slope intercept form, y = -3x + 26.
To graph the line, first make a table of points.
Block towers
| x | y |
| 0 | 26 |
| 1 | 23 |
| 2 | 20 |
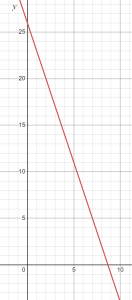
The next number of blocks will be y = 26 – 3x = 26 – 3(3) = 26 – 9 = 17. This can also be gotten by subtracting 3 from Figure 2. 20 – 3 = 17, or by looking at the graph.
Key take-aways:
- If a pattern is decreasing by the same amount each time, the slope of the line is negative.
- The graph of the line will be sloping down as we look from left to right.
Example 4 When will Saul have the same number of blocks on the same turn as the block tower pattern in example 3? That is, when will y = -3x + 26 intersect with y = 2x + 6?
Thus far, we have learned three ways to find when the two patterns will have the same number of blocks on the same turn:
- Make a table of points for each equation and see where on the table the two equations have the same x and y values.
- Graph the two equations and see where the two lines intersect.
- Solve the two equations to find out when the y values are equal. That is, when y = y, we will have -3x + 26 = 2x + 6. We are substituting the expressions -3x +26 and 2x + 6 in for y.
The table of points for the block tower pattern is:
Block towers
| x | y |
| 0 | 26 |
| 1 | 23 |
| 2 | 20 |
And Saul’s table of points is:
Saul’s block pattern
| x | y |
| 0 | 6 |
| 1 | 8 |
| 2 | 10 |
So far, in the two tables, there isn’t a place where both are the same. So let’s use the tables to graph both lines together, to find the intersection.
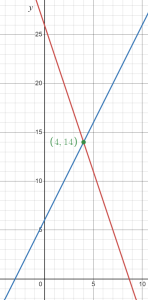
The two lines intersect at (4,14). Another way to say this is that the solution to the system of equations is (4, 14). The two students will have the same number of blocks, 14, on turn 4.
To find this using the tables, we would have to create two more rows. The tables are shown side by side now, so you can more easily see where they are the same.
| Block towers | y = -3x + 26 | Saul’s block pattern | y = 2x + 6 | |
| x | y | x | y | |
| 0 | 26 | 0 | 6 | |
| 1 | 23 | 1 | 8 | |
| 2 | 20 | 2 | 10 | |
| 3 | 17 | 3 | 12 | |
| 4 | 14 | 4 | 14 |
To find this same solution by solving, we set the two equations, y = -3x + 26 and y = 2x + 6, equal to each other, since the two lines intersect where both x and y values are equal.
We get: -3x + 26 = 2x + 6
There are many ways to solve this, but basically you want to get the x terms together on one side of the equation, and the numbers on the other. So, for example, you could subtract 2x from both sides of the equation, and then subtract 26:
-3x + 26 = 2x + 6
-2x -2x
-5x +26 = 6
-26 -26
-5x = -20
/-5 /-5
x = 4
Alternatively, you could add 3x to both sides and subtract 6:
-3x + 26 = 2x + 6
+3x +3x
26 = 5x + 6
-6 -6
20 = 5x
/5 /5
x = 4
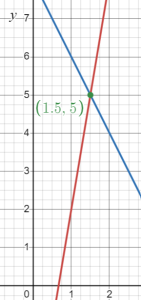
Example 5 Use all three methods: creating a table of points, graphing, and solving, to find the solution to the system of equations, y = -4 + 6x and y = 8 – 2x. Which technique is better for this particular problem?
Note: the term “system of equations” may be new to you. It means two or more equations where we are trying to find a common solution, although there might not always be one.
We can again draw the two tables side by side.
| y = -4 + 6x | y = 8 – 2x | |||
| x | y | x | y | |
| 0 | -4 | 0 | 8 | |
| 1 | -4+6(1) = -4 + 6 = 2 | 1 | 8 – 2(1) = 8 – 2 = 6 | |
| 2 | ? | 2 | ? | |
| 3 | ? | 3 | ? |
The first two values have been filled in. Make sure you are able to find the remaining values, then graph each line.
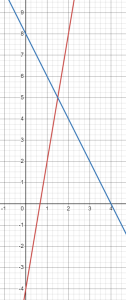
From the graph, we see that the two lines do intersect, but it may be a little difficult to see exactly where. It looks as if the x value of the intersection point is between 1 and 2. The table does not show us an exact value, either.
| y = -4 + 6x | y = 8 – 2x | |||
| x | y | x | y | |
| 0 | -4 | 0 | 8 | |
| 1 | 2 | 1 | 6 | |
| 2t | 8 | 2 | 4 | |
| 3 | 14 | 3 | 2 |
Let’s try solving next, to see if we can get a more precise value.
We have y = -4 + 6x and y = 8 – 2x, and we are looking to see when the x and y-values are the same. So we want to find when y = y. We substitute each expression in for y, and we get
-4 + 6x = 8 – 2x
We start by getting the x terms together on one side, the numbers on the other side:
-4 + 6x = 8 – 2x
+ 2x +2x
-4 + 8x = 8
+4 +4
8x = 12
/8 /8
x = 1.5
To find the y-value, let x = 1.5 in either equation:
y = -4 + 6x = -4 + 6(1.5) = -4 + 9 = 5
(If you use the other equation, you will also get 5).
Thus, the solution to the system of equations is (1.5, 5)
Example 6 Use the solving method to find the solution to our original equations from Saul and Gabi: y = 2x + 6 and y = 2x + 8.
We want to find when the y values are equal, so we let y = y, which is the same as 2x + 6 = 2x + 8. We then gather all the x terms on one side, the numbers on the other:
2x + 6 = 2x + 8
-2x -2x
6 = 8
At this point, we can stop, because we have done away with all the x values. Is the statement we have now true or false? That is, is 6 = 8 true?
No, 6 = 8 is never true, no matter what value for x we have. There is no solution. Why? Because the two lines never intersect because we have parallel lines.