A 2.5  Algebra Topics – Simple Algebraic Fractions; Simplifying, Adding and Subtracting

Kathleen Offenholley; Fatima Prioleau

A 2.5 Algebra Topics – Simple Algebraic Fractions; Simplifying, Adding and Subtracting

Chapter 2 Section A5

Algebra Topics – Simple Algebraic Fractions; Basic Simplifying, Adding and Subtracting

Elementary Education – Connection to simplifying, adding and subtracting numerical fractions

What is an Algebraic Fraction?

An algebraic fraction is a fraction with an algebraic expression in the top (numerator), bottom (denominator), or both. Examples include $\frac{2x}{6}$ and $\frac{x+2}{x+4}$ . These are also often called rational expressions, since rational means in a ratio, or fraction.

Simplifying Algebraic Fractions

In the previous section, we learned how to simplify fractions such as $\frac{6}{15}$ by dividing top and bottom by the same number:

$\frac{6 \div 3}{15 \div 3} = \frac{2}{5}$

In the same way, we can simplify $\frac{2x}{6}$ by dividing the top and bottom by the same number. Since both 2 and 6 are both divisible by 2, we get:

$\frac{2x}{6} = \frac{2x \div 2}{6 \div 2} = \frac{x}{3}$

As with any statement about one algebraic expression equal to another, we should be able to replace the variable with any value, and have the equation still be true. This means that the statement $\frac{2x}{6} = \frac{x}{3}$ is true for any value of x.

For example, if x = 10, we get $\frac{2(10)}{6} = \frac{10}{3}$ . This is true, because $\frac{20}{6} =\frac{10}{3}$ (we can simplify the first fraction by dividing by $\frac{2}{2})$ .

if x = 5, we get $\frac{2(5)}{6} = \frac{5}{3}$ . This is true, because $\frac{10}{6} = \frac{5}{3}$ , again simplifying by dividing by $\frac{2}{2}$ .

If we let x be any number, the first fraction will still simplify to the second.

How would we simplify a fraction like $\frac{x+2}{x+4}$ ? Can we cancel the x terms, resulting in $\frac{2}{4}= \frac{1}{2}$ ?

If this is true, then we can let x be any number in the expression $\frac{x+2}{x+4}$ and we should get $\frac{1}{2}$ .

Let’s try x = 2. $\frac{2+2}{2+4} = \frac{4}{6}$ . But the fraction $\frac{4}{6}$ simplifies to $\frac{2}{3}$ , not $\frac{1}{2}$ . Since this does not work when x = 2, it is not true — because it has to be true for all values of x. It is not true that you can simplify by removing the x terms.

To simplify fractions:

We can divide numerator and denominator by common factors (multiplied parts).
We cannot remove or cancel added or subtracted terms.

Why can we cancel factors (multiplied parts), but not terms (added parts)? Because multiplication and division are very closely related — they are essentially opposites of each other — while addition and subtraction are very different from division, a whole step away in the order of operations.

Example 1 Simplify 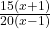$\frac{15(x+1)}{20(x-1)}$ .

In this fraction, we see that the 15 is multiplying in the numerator (top) and the 20 is multiplying in the denominator (bottom), so that means that 15 and 20 are factors. We can simplify by dividing both by 5:
$\frac{15(x+1) \div 5}{20(x-1)\div 5} = \frac{3(x+1)}{4(x-1)}$

We cannot simplify any further by “canceling” the x’s or the 1’s, since those terms are being added and subtracted, not multiplied.

Question: Now you try!

Example 2 Simplify 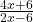$\frac{4x+6}{2x-6}$ .

We can’t simplify this fraction by canceling the 6’s, since the 6’s are being added or subtracted, not multiplied. But we might notice that both the numerator and denominator are divisible by 2. We can rewrite $4x+6$ by factoring out the common factor of 2 from each term. We get that $4x+6 = 2(2x +3)$ . This works because if we multiply 2 by (2x+3), we get back our original expression. That is, $2(2x+3) = 4x+6$ .

Similarly, we can factor 2 from $2x-6$ . What would you get?

That is, imagine dividing both $2x$ and $6$ by 2.

What would you get?

You would have 2 outside the parenthesis, and what would be left inside?

[Spoiler space]

You would get $2(x-3)$ , which is the same as $2x-6$ .

Now we have $\frac{4x+6}{2x-6} = \frac{2(2x+3)}{2(x-3)}$ .

We can now simplify by dividing both top and bottom by 2:

$\frac{4x+6}{2x-6} = \frac{2(2x+3)}{2(x-3)} = \frac{2x+3}{x-3}$ .

We could have also simplified the original fraction by dividing every term by 2:

$\frac{4x+6}{2x-6} = \frac{4x \div 2+6 \div 2}{2x \div 2 - 6 \div 2} = \frac{2x+3}{x-3}$ .

Notice that when you divide without factoring first, you have to divide every term because you are basically having to use the distributive property. The distributive property must be used when we mix multiplication or division with addition and subtraction. If everything is already factored, you are only mixing multiplication and division, which does not require the distributive property.

Question: Now you try!

Example 3 Simplify 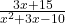$\frac{3x + 15}{x^2 + 3x - 10}$ .

To simplify this fraction, we must first turn the added and subtracted terms into factors. The denominator of the fraction has three terms, so it’s a trinomial. It begins with the term, $x^2$ . You might remember back in a previous algebra section, where we found a pattern when we multiplied two binomials. Here are some examples to help you remember:

$(x + 2)(x + 3) = x^2 + 3x + 2x + 6 = x^2 + 5x + 6$

$(x + 4)(x + 7) = x^2 + 7x + 4x + 28 = x^2 + 11x + 28$

$(x - 3)(x + 5) = x^2 + 5x - 3x - 15 = x^2 + 3x - 15$

In each case, look at how the two numbers multiply to get the end term of our answer, and add to get the coefficient of the middle term.

$(x + 2)(x + 3) = x^2 + 5x + 6$ In this one, 2 + 3 = 5, the middle term, and 2 × 3 = 6, the end term.

$(x + 4)(x + 7) = x^2 + 11x + 28$ In this one, 4 + 7 = 11, the middle term, and 4 × 7 = 28, the end term.

$(x - 3)(x + 5) = x^2 + 5x - 3x - 15 = x^2 + 3x - 15$ In this one, -3 + 5 = 2, the middle term, and -3 × 5 = -15, the end term.

So, to factor the denominator of our fraction, $\frac{3x+15}{x^2+3x-10}$ , think of what multiplies to equal the end term, -10, and adds to get 3, the middle term.

To do this, use the problem solving strategy of listing all the pairs that multiply to get -10:

-1 × 10

1 × -10

2 × -5

-2 × 5

Which of these pairs also adds to get 3?

-1 + 10 = 9

1 + -10 = -9

2 + -5 = -3

-2 + 5 = 3

The last pair adds to get 3. Thus we have, $x^2 + 3x - 10 = (x - 2)(x + 5)$ .

The numerator (top) of the fraction, $3x + 15$ can be factored by noticing that both terms are divisible by 3, so we get $3x + 15 = 3(x + 5)$ .

Now we have: $\frac{3x + 15}{x^2 + 3x - 10} = \frac{3(x + 5)}{(x - 2)(x + 5)}$

Since numerator and denominator now have a common factor of x + 5, we can simplify the fraction to $\frac{3}{x - 2}$ .

Question: Now you try!

Adding and Subtracting Algebraic Fractions with the Same (Common) Denominators

In the previous section, we saw that we could add fractions that have the same denominators by keeping the common denominator, and adding only the numerators.

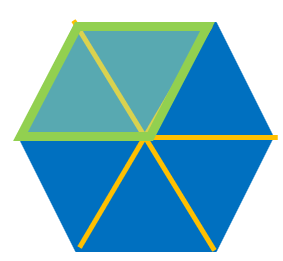
For example, this picture shows that $\frac{1}{6} + \frac{1}{6} = \frac{2}{6}$

We can see this visually because there are 6 triangles in this hexagon, so 1 triangle = 1/6, and we have 1 triangle + 1 triangle = 2 triangles.

Note that we do not add the denominators to get $\frac{1}{6} + \frac{1}{6} = \frac{2}{12}$ .

That answer would be a little strange, because $\frac{2}{12}$ simplifies to $\frac{1}{6}$ , so that would mean that $\frac{1}{6} + \frac{1}{6} = \frac{1}{6}$ .

It makes much more sense that $\frac{1}{6} + \frac{1}{6} = \frac{2}{6}$ , and $\frac{2}{6}$ simplifies to $\frac{1}{3}$ . We can see in the picture that $\frac{1}{3}$ of the hexagon is shaded.

Addition of fractions that have the same denominators is very similar to adding like terms:

$1x + 1x = 2x$ not $1x + 1x = 2x^2$

$1x^2 + 1x^2 = 2x^2$ not $1x^2 + 1x^2 = 2x^4$

To add fractions with the same algebraic denominators, add the numerators and keep the denominators the same. For example:

$\frac{5}{2x} + \frac{3}{2x} = \frac{8}{2x}$

$\frac{1}{x+3} + \frac{2}{x+3} = \frac{3}{x+3}$

The first of these can be simplified: $\frac{8}{2x} = \frac{4}{x}$ , the other fraction, $\frac{3}{x+3}$ cannot be simplified.

Example 4 a. Add 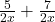$\frac{5}{2x}+ \frac{7}{2x}$ . b. Add 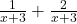$\frac{1}{x+3} + \frac{2}{x+3}$ . Simplify the results if possible.

$\frac{5}{2x} + \frac{7}{2x} = \frac{12}{2x}$

$\frac{1}{x+3} + \frac{2}{x+3} = \frac{3}{x+3}$

The first of these can be simplified: $\frac{12}{2x} = \frac{6}{x}$ . The other fraction, $\frac{3}{x+3}$ cannot be simplified. The 3’s cannot be cancelled, since they are added terms, not multiplied factors.

Question: Now you try! Several simple mult. choice with simple adding and simplifying

Adding and Subtracting Algebraic Fractions with Unlike Denominators

In the previous section, to add $\frac{1}{2} + \frac{1}{3}$ , we rewrote each as 6ths:

$\frac{1 \times 3}{2 \times 3}+\frac{1 \times 2}{3 \times 2} = \frac{3}{6}+ \frac{2}{6} = \frac{5}{6}$

Notice that we multiplied the first fraction by 3/3, and 3 is the denominator of the second fraction. We multiplied the second fraction by 2/2, and 2 is the denominator of the first fraction. This method is a very quick and easy way we can always use to get a common denominator, though it will not always get us the smallest common denominator.

Written algebraically, if we have $\frac{1}{a} + \frac{1}{b}$ , we can multiply the first fractions by b/b, and the second by a/a:

$\frac{1}{a} + \frac{1}{b} = \frac{1 \times b}{a \times b}+\frac{1 \times a}{b \times a} = \frac{b}{ab}+ \frac{a}{ab} = \frac{b+a}{ab}$

Notice that when we add the numerators (the tops), we can’t combine b and a, so we just show that they are being added.

Example 5 a. Add 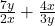$\frac{7y}{2x} + \frac{4x}{3y}$ . b. Subtract $\frac{3x}{14y^2} - \frac{5}{7ya^5}$ . c. Subtract $\frac{4}{x+3} - \frac{2}{x+5}$ .

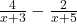For each example, simplify the results if possible.

a. Add $\frac{7y}{2x} + \frac{4x}{3y}$

Notice that the first fraction has $2x$ in the denominator, while the second has $3y$ in the denominator.

So we can multiply the first fraction by $3y$ in both numerator and denominator, and the second by $2x$ in both numerator and denominator:

$\frac{7y}{2x} + \frac{4x}{3y} = \frac{(7y)(3y)}{(2x)(3y)} + \frac{(4x)(2x)}{(3y)(2x)}$

Multiply out the numerators and denominators, then add:

$\frac{(7y)(3y)}{(2x)(3y)} + \frac{(4x)(2x)}{(3y)(2x)} = \frac{21y^2}{6xy} + \frac{8x^2}{6xy} = \frac{21y^2 + 8x^2}{6xy}$

The numerator of the fraction cannot be added any more than that, since we do not have like terms. The fraction cannot be simplified, since there is no number or variable that can divide into both terms in the numerator, and into the denominator.

b. Subtract $\frac{3x}{14y^2} - \frac{5}{7a^5y^2}$

The same rules apply for subtraction as for addition. Notice that the first fraction has $14y^2$ in the denominator, while the second has $7a^5y^2$ . So we can multiply the first fraction by $7a^5y^2$ in both numerator and denominator, and the second by $14y^2$ in both numerator and denominator:

$\frac{3x}{14y^2} - \frac{5}{7a^5y^2} = \frac{(3x)(7a^5y^2)}{(14y^2)(7a^5y^2)} - \frac{(5)(14y^2)}{(7a^5y^2)(14y^2)}$

When we multiply out the denominators, they should end up being equal to each other, since $(14y^2)(7a^ 5y^2) = (7a^5y^2)(14y^2) = 98a^5y^4$ .

Multiplying out the numerators and denominators, we now have:

$\frac{(3x)(7a^5y^2)}{(14y^2)(7a^5y^2)} - \frac{(5)(14y^2)}{(7a^5y^2)(14y^2)} = \frac{21a^5xy^2}{98a^5y^4} - \frac{70y^2}{98a^5y^4} = \frac{21a^5xy^2 - 70y^2}{98a^5y^4}$

Notice that we do not have like terms in the numerators (tops), so we can’t subtract them, instead, we just show that they are being subtracted.

This fraction can be simplified: the numerator $21a^5xy^2 - 70y^2$ has $y^2$ in both terms, and the number 7 is a factor in both terms, so we can factor out $7y^2$ to get $21a^5xy^2 - 70y^2 = 7y^2(3a^5x - 10)$ .

Next, we can simplify by dividing $7y^2$ from both numerator and denominator:

$\frac{21a^5xy^2 - 70y^2}{98a^5y^4} = \frac{7y^2(3a^5x - 10) \div 7y^2}{98a^5y^4 \div 7y^2} = \frac{3a^5x - 10}{14a^5y^2}$

(Or you could think of subtracting the exponents: $\frac {y^2}{y^4} = y^2^-^4 = y^-^2 = \frac {1}{y^2}$ )

c. Subtract $\frac{4}{x+3} - \frac{2}{x+5}$

To subtract, we need a common denominator. Could we just add 2/2 to the first fraction?

No, $\frac{4+2}{x+3+2}$ does not work to give an equivalent fraction, since adding to a fraction changes its size. Instead, we have to multiply the fraction by a form of 1, since that keeps the fraction the same.

Tip: multiply the numerator and denominator of each fraction by the whole denominator of the other fraction. That is, multiply the first fraction by $\frac{x+5}{x+5}$ , and multiply the second fraction by ….?

[spoiler space! Try it out]

…..

….

Multiply the first fraction by $\frac{x+5}{x+5}$ , and multiply the second fraction by $\frac{x+3}{x+3}$ .

We get $\frac{4}{x+3} (\frac{x+5}{x+5}) - \frac{2}{x+5} (\frac{x+3}{x+3}) = \frac{(4)(x+5)}{(x+3)(x+5)} - \frac{(2)(x+3)}{(x+5)(x+3)}$

Distribute the multiplication in each numerator (top). Leave the denominator as it is (more on why in a moment!)

$= \frac{4x+20}{(x+3)(x+5)} - \frac{2x+6}{(x+5)(x+3)}$

Now we can add the numerators, $(4x + 20) - (2x + 6) = 4x + 20 - 2x - 6= 4x - 2x + 20 - 6 = 2x + 14$

The answer is $\frac{2x+ 14}{(x+3)(x+5)}$

Finally, factor the top (numerator). You can divide both 2x and 14 by 2, so we get 2(x+7) on the top.

Our final, factored answer is $\frac{2(x+ 7)}{(x+3)(x+5)}$ , which cannot be simplified since the factors in the numerator and denominator are not the same. But if we had something like $\frac{2(x+ 3)}{(x+3)(x+5)}$ or $\frac{2(x+ 5)}{(x+3)(x+5)}$ , then we would have common factors we could divide out. That’s why we keep the denominator factored — just in case we can simplify at the end!

Question: Now you try! Several simple mult. choice with simple adding and simplifying

Another way to get a common denominator is to multiply each fraction by the factors it is missing that are in the other denominator. For example, to add the fractions $\frac{1}{6} + \frac{1}{4}$ , we might notice that 6 = 2 × 3 and 4 = 2 × 2. The first number has a factor of 3 in it and the other one does not. The second number has two factors of two, while the first one only has one. The first number six, is missing a factor of 2. The second number, 4, is missing a factor of 3. Multiply each by those “missing” factors to get a common denominator:

$\frac{1}{6} + \frac{1}{4} = \frac{1 \times 2}{6 \times 2} + \frac{1 \times 3}{4 \times 3} = \frac{2}{12} + \frac{3}{12} = \frac{5}{12}$

Of course, you could also still use the other method, of multiplying each fraction by the whole other denominator, you will just have to simplify at the end:

$\frac{1}{6} + \frac{1}{4} = \frac{1 \times 4}{6 \times 4} + \frac{1 \times 6}{4 \times 6} = \frac{4}{24} + \frac{6}{24} = \frac{10}{24} = \frac{5}{12}$

Example 6 Add or subtract by multiplying by the factors that each denominator is missing, instead of by the whole other denominator: a. $\frac{9x}{a^2y^2} + \frac{2}{a^3y}$ , b. $\frac{3x}{14y^2} - \frac{5}{7a^5y^2}$

a. $\frac{9x}{a^2y^2} + \frac{2}{a^3y}$

The first fraction has a² in the denominator, while the second one has a³. That means the first fraction needs another factor of a.

The second fraction has y in the denominator, while the first has y². That means the second fraction needs another factor of y.

$\frac{9x}{a^2y^2} + \frac{2}{a^3y} = \frac{9x \times a}{a^2y^2 \times a} + \frac{2 \times y}{a^3y \times y} = \frac{9xa}{a^3y^2} + \frac{2y}{a^3y^2} = \frac{9xa + 2y}{a^3y^2}$

b. $\frac{3x}{14y^2} - \frac{5}{7a^5y^2}$

The first fraction has y ² in the denominator, like the second fraction, but it doesn’t have a⁵. That means the first fraction needs a⁵.

The first fraction has 14 = 2 × 7 in the denominator, while the second one has 7. That means the second fraction needs a factor of 2.

$\frac{3x}{14y^2} - \frac{5}{7a^5y^2} = \frac{3x \times a^5}{14y^2 \times a^5} - \frac{5 \times 2}{7a^5y^2 \times 2} = \frac{3a^5x}{14a^5y^2} - \frac{10}{14a^5y^2} = \frac{3a^5x - 10}{14a^5y^2}$

You may notice that this is the same answer we got as in example 5b, where we multiplied by the whole other denominator, instead of just by what was missing. But there, we had to simplify in the end, and here we did not.

Question: Now you try! Several simple mult. choice with simple adding and simplifying that can be reduced or added only with what’s missing

A 2.5 Algebra Topics – Simple Algebraic Fractions; Simplifying, Adding and Subtracting

Chapter 2 Section A5

What is an Algebraic Fraction?

Simplifying Algebraic Fractions

Example 1 Simplify $\frac{15(x+1)}{20(x-1)}$ .

Example 2 Simplify $\frac{4x+6}{2x-6}$ .

Example 3 Simplify $\frac{3x + 15}{x^2 + 3x - 10}$ .

Adding and Subtracting Algebraic Fractions with the Same (Common) Denominators

Example 4 a. Add $\frac{5}{2x}+ \frac{7}{2x}$ . b. Add $\frac{1}{x+3} + \frac{2}{x+3}$ . Simplify the results if possible.

Adding and Subtracting Algebraic Fractions with Unlike Denominators

Example 5 a. Add $\frac{7y}{2x} + \frac{4x}{3y}$ . b. Subtract $\frac{3x}{14y^2} - \frac{5}{7ya^5}$ . c. Subtract $\frac{4}{x+3} - \frac{2}{x+5}$ .

For each example, simplify the results if possible.

Example 6 Add or subtract by multiplying by the factors that each denominator is missing, instead of by the whole other denominator: a. $\frac{9x}{a^2y^2} + \frac{2}{a^3y}$ , b. $\frac{3x}{14y^2} - \frac{5}{7a^5y^2}$

License

Share This Book

Chapter 2 Section A5

What is an Algebraic Fraction?

Simplifying Algebraic Fractions

Example 1 Simplify .

Example 2 Simplify .

Example 3 Simplify .

Adding and Subtracting Algebraic Fractions with the Same (Common) Denominators

Example 4 a. Add . b. Add . Simplify the results if possible.

Adding and Subtracting Algebraic Fractions with Unlike Denominators

Example 5 a. Add . b. Subtract . c. Subtract .

For each example, simplify the results if possible.

Example 6 Add or subtract by multiplying by the factors that each denominator is missing, instead of by the whole other denominator: a. , b.

License

Share This Book

Example 1 Simplify $\frac{15(x+1)}{20(x-1)}$ .

Example 2 Simplify $\frac{4x+6}{2x-6}$ .

Example 3 Simplify $\frac{3x + 15}{x^2 + 3x - 10}$ .

Example 4 a. Add $\frac{5}{2x}+ \frac{7}{2x}$ . b. Add $\frac{1}{x+3} + \frac{2}{x+3}$ . Simplify the results if possible.

Example 5 a. Add $\frac{7y}{2x} + \frac{4x}{3y}$ . b. Subtract $\frac{3x}{14y^2} - \frac{5}{7ya^5}$ . c. Subtract $\frac{4}{x+3} - \frac{2}{x+5}$ .

Example 6 Add or subtract by multiplying by the factors that each denominator is missing, instead of by the whole other denominator: a. $\frac{9x}{a^2y^2} + \frac{2}{a^3y}$ , b. $\frac{3x}{14y^2} - \frac{5}{7a^5y^2}$