A 2.6 Exponential Equations: Graphing and Applications
Chapter 2 Section A6
Algebra Topics – Graphing Non-linear Equations; Exponential Equations and Applications
Exponential Growth
We have previously looked at growth that adds the same amount each time. For example, in this table, we start at the number 1, and then add 2 each time:
| x | y |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
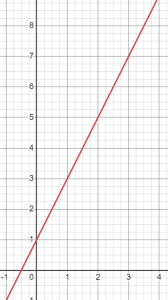
By the time we have gotten to x = 4, we have added: 1 + 2 + 2 + 2 + 2 = 9. That is, we have added on 2, four times: 1 + 2(4) = 9. Our equation is y = 1 + 2x, with a starting number of 1 and the repeated addition of two expressed as multiplication.
The graph of this table shows a straight line, with a slope of 2:
What happens if instead, we start at 1 and repeatedly multiply by 2?
| x | y |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
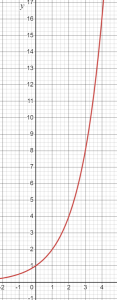
Now, by the time we have gotten to x = 4, we have multiplied: 1 × 2 × 2 × 2 × 2 = 16. That is, we have multiplied by 2, four times: 1 × 24 = 16. Our equation is y = 1 × 2x, with a starting number of 1 and the repeated multiplication by two expressed as an exponent. We do not need to write the 1, we can instead write y = 2x, but leaving the 1 there reminds us of what our starting number is.
Exponential growth occurs when a patterns grows by repeated multiplication.
The graph of this table shows curve, growing much more quickly than the line.
Example 1 For each table below, identify whether the growth is linear or exponential, find each equation, and graph.
Table A
| x | y |
| 0 | 4 |
| 1 | 12 |
| 2 | 36 |
| 3 | 108 |
Table B
| x | y |
| 0 | 4 |
| 1 | 7 |
| 2 | 10 |
| 3 | 13 |
Table A shows exponential growth, starting at 4 and multiplying by 3 each time. The equation is y = 4• 3x.
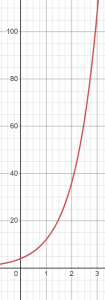
Table B shows linear growth, starting at 4 and adding 3 each time. The equation is y = 4 + 3x.
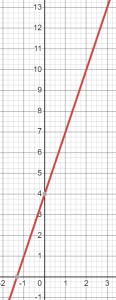
Notice how much faster the first graph is growing, already above 100 when x = 3.
What kinds of things grow exponentially?
Population growth, bacterial growth, the spread of the flu, or a video that “goes viral” are all examples of exponential growth. Why? Because if one person shares a video with 10 friends, and they each share that same video with ten friends, the number of views is multiplying by ten each time. If one cat has 6 kittens, and each of those kittens has 6 kittens, the number of kittens is multiplying by 6 each generation.
Exponential growth is generally very fast growth.
However, money can also grow exponentially — but if it grows by a low percent, like 2%, it will not grow quickly.
For example, if I have $1000 at 2% yearly interest, since 2% of $1,000 is only .02 (1000) = $20 of interest, so we will only have $1,020 after a year. If we leave that money in the bank, and the next year we get 2% of $1,020, that will be .02 (1020) = $20.40, so now we will have $1,040.40 in the bank — and that’s after two years! The year after that, we will have 2% of 1040.40 = .02 (1040.40) = $20.808 in interest, for a total of $1061.208. The table below shows the money each year:
| x, number of years | y, amount in the bank |
| 0 | $1000 |
| 1 | $1020 |
| 2 | $1040.40 |
| 3 | $1061.208 |
A faster way to calculate the amount we will have each year, instead of adding the interest, is to multiply by 1.02 each year, or 102%. So for example, $1000(1.02) = $1020, and then $1020(1.02) = $1040.4, etc.
| x, number of years | y, amount in the bank |
| 0 | $1000 |
| 1 | $1000(1.02) = $1020 |
| 2 | $1020(1.02) = $1040.40 |
| 3 | $1040.40(1.02) =$1061.208 |
Why does this work? Because $1,000(1.02) is the same as 1000(1 + .02) = 1000 + 20, using the distributive property.
Each year, we again multiply our bank balance by 1.02. Thus, we have exponential growth.
To figure out how much money is in the bank after 3 years, we can calculate $1,000(1.02)3 = $1,1061.21 (rounded off to the nearest cent), just as in the table, above.
The equation for the amount of money, y, in the bank after x years is y = 1000 (1.02)x. You can see that the starting number is 1,000, and that the rate of interest is 2% (the .02).
Example 2 Write the equation for how much money you will have in the bank after x years, if you start with a balance of $3000 and the interest rate is 8%.
If we have an interest rate of 8%, that’s the same as multiplying by 1.08. Our starting number is $3000, so the exponential equation is y = 3000(1.08)x
Example 3 Write the equation for how much money you will have in the bank after x years, if you start with a balance of $4000 and the interest rate is 5%. Then use the equation to find the amount of money you will have after 7 years.
If we have an interest rate of 5%, that’s the same as multiplying by 1.05. Our starting number is $4000, so the exponential equation is y = 4000(1.05)x. After 7 years, we will have y = 4000(1.05)7 = $5,628.40 (rounded to the nearest cent).
 Calculator Note
Calculator Note
If you type 4000(1.05)7 into your calculator, it might not understand that the ( ) mean that you want it to multiply. So you should type in the expression 4000 × 1.05^7 (or you might need to find the calculator button that says yx instead of ^). Try it to make sure you get the correct answer! If you don’t, you may need to type in 1.05^7 first, then multiply by 4000.
Negative exponents
So far, we have talked about integer exponents, which give us very fast exponential growth. We have talked about decimal exponents, such as with interest in the bank, that gives us slower growth. The one type of number we not yet explored is what happens when we have negative exponents. Do we end up with negative numbers?
Let’s look at one of the graphs. This is the graph of the equation y = 2x.

The negative values for x are on the left side of the graph. What do we see for the y values? Are they negative? Do they go below zero? If we zoom in on the bottom part of the graph, we can see that as the x values go more and more negative, the curve seems headed closer and closer to y = 0. But y will never actually get to zero!
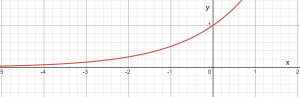
A table of values will show us why:
| x | y = 2x |
| 0 | 20 = 1 |
| -1 | 2-1 = |
| -2 | 2-2 = |
| -3 | 2-3 = |
| -4 | 2-4 = |
With negative exponents, we are getting smaller and smaller fractions, which will get close to zero, but never actually equal zero.