Sec. 1.1 – Introduction to Base Ten Additive, Multiplicative and Place Value Numeration Systems
Chapter 1, Section 1
Math Topics – Introduction to Base Ten Additive, Multiplicative and Place Value Numeration Systems; Chinese and Egyptian Numerals; the Abacus; Hindu Arabic
Elementary Education – Dispelling Math Myths; Children Counting
Math Myths
- There is only one right way to do math.
- There is only one right answer.
- Boys are better at math.
- The person who gets the answer fastest is the smartest at math.
- Certain ethnic or racial groups are really good at math.
- Some ethnic or racial groups can’t do math.
- Some people are good at math and some people are good at reading. People are not good at both.
- “I’m just not good at math”
Each of these math myths is wrong, and can even be harmful. For example, when we think there is only one right way to do math, we can stifle creativity and exploration in math. It’s important to recognize that there are many ways to get to a correct answer – even many correct answers, depending on the situation. Later in this and the next chapter, we will see different ways to add, subtract, multiply and divide that may be better for students with different learning styles, and we will look at computation methods that various cultures have used and still use today.
The myth that boys are better at math persists even today, despite the fact that studies show that girls can do math just as well as boys, sometimes better. When a teacher has the idea that some kinds of children can’t do math as well, this can influence how a child performs in class. The myth of being inferior is often internalized by the student. Several studies by Claude Steele and colleagues show that African American college students can do worse on standardized tests when they perceive that their race is being emphasized, and that women may do worse than men in mathematics when they are told that the test shows gender differences. When the students did not think they were being judged by race or gender, the tests showed no difference between groups. Even the so-called “positive” stereotype that Asians are better at math can be harmful, especially to Asian children who find themselves struggling with math.
Finally, it’s important to remember that no one is born being good or bad at math, and that most people’s brains are wired to be able to do just about anything (the whole “left brain/right brain” dichotomy is a myth, too). Like most subjects in school, the more work you do in it, the better you get. The key is that our students must be motivated to do the work that helps them learn more.
As we work on the math in this and the next chapters, ask yourself, “What will make math fun and interesting for my students, so they will be motivated to do more?”
Question: Has there been a time in your life when you believed one of these myths? Are there some that you still believe?
Let’s put all the math myths in the trash, where they belong. Then hit “check” to see how you scored.
|
|
Ancient Egypt
The Ancient Egyptians lived mostly along the Nile river in North East Africa. Even as early as 3000 BCE (over 5,000 years ago), we have evidence that they had writing and written numerals, using hieroglyphs. Artifacts like the Rhind Papyrus and the Moscow Papyrus show that the scribes calculated area and volume, figured out problems that had unknowns (a precursor to our modern algebra) and worked with various forms of unit fractions. The problems they solved included many that involved figuring out the quantity of grain needed to make bread or beer, and how productive a worker could be (for example, one problem includes the number of shoes a shoe maker could produce.) Keep in mind that the few fragile papers that survived until now only show a small part of all the mathematics that the Egyptians did.

Paul James Cowie (Pjamescowie) [Public domain], via Wikimedia Commons
The Egyptian Number System
The number system the Egyptians used from about 3,000 BCE to 1,000 CE used hieroglyphs. Each power of 10 was a different symbol. The Egyptian system was additive. That is, to get the value of a number, you add up the values of all the symbols used. The Egyptians did not have a symbol for zero.
Egyptian Symbols
| Value | 1 | 10 | 100 | 1,000 | 10,000 | 100,000 | 1,000,000 |
| Symbol | | | ||||||
| Description | Line or Staff | Horse Shoe | Coil or Scroll | Flower | Raised Finger | Tadpole | Amazed Person |
Example 1 Find the value for the number below.
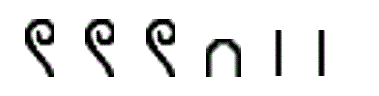
In this number, we have three coils (also called scrolls). Each coil is worth 100. We have one horse shoe, worth 10, and two lines, each worth one. Since this is an additive system, we add the values of the symbols: 100+100+100+10+1+1 = 312
Example 2 How would we write the number 12,040 in Egyptian?
Find the symbols for each place value. Begin with the 1. This number is in the 10,000 place, so we will need one raised finger. Next, the 2 is in the 1,000 place, so we will need 2 flowers. Finally, we will need 2 horse shoes.
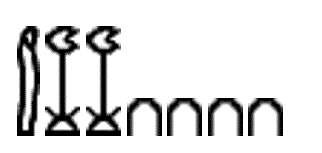
12,040 = 10,000+1,000+1,000+10+10+10+10
Notice that we do not need a zero – we simply leave out the objects for those places. Also notice that we don’t use 12 flowers. This is a base ten system, so we never use more than nine of any object. If we reach ten of an object, we use the next higher symbol. The exception to this is numbers greater than one million, since one million was their largest symbol.
Tip If you have trouble thinking about which place value each part of the number is in, line it up with the base ten place value chart.
| Millions (Amazed Person) |
Hundred Thousands (Tadpole) | Ten Thousands (Raised Finger) | Thousands (Flower) | Hundreds (Scroll) | Tens (Horse Shoe) |
Ones (Line) |
| 1,000,000 | 100,000 | 10,000 | 1,000 | 100 | 10 | 1 |
| 1 | 2 | 0 | 4 | 0 |
The Abacus
The abacus was used in Ancient Greece, Egypt and Persia, and is also still used in many places today. China, Japan, and Russia each have slightly different versions of the abacus, but they all use base ten, and many have a special position or marker to show five.

The picture above shows a Chinese abacus. The top row of beads is worth 5 each; on the bottom, each bead is worth 1. The beads pushed to the middle bar show the number. This abacus shows the number 37,925: three beads on the left, then 2 beads + a five bead = 7, then 4 beads + a five bead = 9, then 2 beads, then just a 5 bead.
This online abacus http://www.mathematik.uni-marburg.de/~thormae/lectures/ti1/code/abacus/sanpan.html is a great way to see how numbers are made!
This video of students using an abacus shows how they can beat a BBC reporter who is using a calculator:
And here is a great video of an abacus champion beating a calculator user – and her abacus is invisible!
This is a great way to see the superiority of the abacus — the abacus helps your fingers understand the math!
Question: Now you try!
The Traditional Chinese Number System
Chinese mathematics developed as early as the 11th century BCE. Over centuries, the Chinese developed negative numbers, decimals and used algebra and trigonometry. They were one of the earliest civilizations to develop a zero.
Although most people in China now use the same number system we use in Europe and the United States, the Hindu Arabic Number System (1, 2, 3….), students still also learn the traditional symbols.
The Traditional Chinese Number System is multiplicative in base ten. A number from 1 to 9 is multiplied by a power of 10. The multiplying is done in pairs and the results are added together. A zero is used to show an empty place value in the middle of a number, but it is not needed at the end of a number.
Traditional Chinese Symbols
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 100 | 1000 | 10,000 | |
| Symbol | 零 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 | 百 | 千 | 萬 |
Example 3 Write 312 in traditional Chinese.
三 3
百 × 100
一 1
十 × 10
二 2
Each place value except for the ones place has a multiplier. For example, for the number 312, the first digit, 3, is in the hundreds place, so must be multiplied by 100, the next digit, 1, is in the tens place, so must be multiplied by 10. The 2, in the ones place, can be written without showing the multiplication by 1.
Example 4 Write 12,040 in traditional Chinese.
一 1
千 × 10,000
二 2
千 × 1,000
零 (no multiplier needed)
四 4
十 × 10
(no ones place needed)
A zero in the middle of a number must be represented by the symbol for zero, but the multiplier is not needed.
The zero at the end is not needed.
Question: Now you try!
Education Note: The way we say our numbers can influence how we calculate with them. In English, the numbers 11 and 12 have their own special words (“eleven” and “twelve”) but in Chinese, the word for 11 is “ten one” and 12 is “ten two.” Studies of children have shown that English-speaking children have a harder time adding and subtracting with 11 and 12, than do Chinese children.
Hindu Arabic
We call our own system of numeration Hindu Arabic, because it was first invented in India by the Hindus, then exported throughout the world by Arab traders. Our system is base ten, place value, and has a zero.
A note about remembering the numeration systems: You should know how the traditional Chinese and Egyptian systems work (what type of system, what base and whether the system has a zero), but you do not have to know the symbols (or even be able to draw them very well!) You will be expected to remember the symbols for Mayan and Babylonian numbers (which will be introduced in the next sections).

Children Counting
Young children can learn the names for the numbers and be able to point to objects when they are counting. Yet in what Piaget called the pre-operational stage of development (about age two to seven), they may not associate the number with the idea of quantity. Both these videos show young children counting. In the first video, the child first counts seven objects, but then very confidently says that there are four:
In this second video, a child compares two rows of five coins. Like most children his age, he believes there are “more” when the coins are spread out.
Homework
Check with your professor whether you are using imathas.helpyourmath.com system or the homework, below. If you are using imathas.helpyourmath.com do not use the homework below. If you are using the homework sets below, please show all your work on each problem, and check your answers.