Sec. 1.2 – The Mayan Number System, Place value in Base 20
Chapter 1, Section 2
Math Topics – The Mayan Number System, Place Value in Base 20
Elementary Education – Place Value in Base Ten
Base Ten Place Value

Base ten is a natural place value for humans, since we have ten fingers, so it is natural for us to want to group by tens. Many number systems across many civilizations and centuries have used ten as their base, including the Chinese and Egyptian number systems we saw in the previous section. But the Mayan system developed using base twenty, also natural to humans, since we have ten fingers and ten toes. Looking at a system that is in a different base from ours will allow you to see our own base ten more clearly. In addition, studying the Mayan civilization is part of the curriculum in 5th grade in the New York City school system, so studying their numbers gives you a chance to broaden that curriculum for your students to include a study of the Mayan numbers.
Mayan Civilization and Mathematics
Excerpted from an article from the University of St. Andrews Math History website by J J O’Connor and E F Robertson.
“[T]he Classic Period of the Maya …spans the period 250 AD to 900 AD, but this classic period was built on top of a civilisation which had lived in the region from about 2000 BC. The Maya of the Classic Period built large cities, around fifteen have been identified in the Yucatán peninsular, with recent estimates of the population of the city of Tikal in the Southern Lowlands being around 50000 at its peak. Tikal is probably the largest of the cities and recent studies have identified about 3000 separate constructions including temples, palaces, shrines, wood and thatch houses, terraces, causeways, plazas and huge reservoirs for storing rainwater. The rulers were astronomer priests who lived in the cities who controlled the people with their religious instructions. Farming with sophisticated raised fields and irrigation systems provided the food to support the population.
“A common culture, calendar, and mythology held the civilisation together and astronomy played an important part in the religion which underlay the whole life of the people. Of course astronomy and calendar calculations require mathematics and indeed the Maya constructed a very sophisticated number system. We do not know the date of these mathematical achievements but it seems certain that when the system was devised it contained features which were more advanced than any other in the world at the time.”
The Mayan Symbols
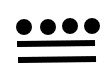
The symbols in the Mayan system start out in an elegantly simple way, with one dot for 1, two dots for 2, and so on up to 5, which was a line.
| 1 | 2 | 3 | 4 | 5 |
| __ |
Many numeration systems used a different symbol for 5, because it is hard to tell how many you have after about six or seven repeated marks. For example, in Mayan symbols, if we write 6 dots: ![]() it is difficult to tell how many dots we have at a glance.
it is difficult to tell how many dots we have at a glance.
Instead, the Mayans wrote a dot with a line under it:
![]()
__
Similarly, the Romans wrote VI for six, instead of writing IIIIII.
Even in modern times, when we use tally marks, we draw a diagonal line across 4 lines to create 5, then one more line for 6.
![]()
Before looking further, see if you can figure out the Mayan numbers up to 19, completing the chart below. The numbers from 1 to 6 have been filled in for you. See if you can figure out the rest!
| 1 | 2 | 3 | 4 | 5 |
| __ | ||||
| 6 | 7 | 8 | 9 | 10 |
__ |
||||
| 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | |
Try to figure out the rest of the numbers yourself, before you page down!
Mayan numbers from 1 to 19
Mayan Place Values
Notice that the symbols in the table, above, stop at 19. The symbol for 20 is not five lines. This is because the Mayan number system was place value, like our system, Hindu Arabic. When they got to 20, they used a separate place value of 20 to create the numbers. For this, a zero was needed. The Mayans were one of the few civilizations to develop a symbol for zero, for which they used the image of a shell:

The symbol is similar to a cowrie shell:

Mayan symbols were stacked to create numbers 20 and higher. The bottom place was the ones place, and above that, the 20’s place:
Example 1 How did the Mayans create 20? What about 40?
To create the Mayan number 20, Mayans placed a one in the 20’s place, and a zero below it, to indicate that there were no ones:
 ← One in the 20’s place = 1 × 20=20
← One in the 20’s place = 1 × 20=20
 ← Zero (a shell) in the ones place, showing no ones
← Zero (a shell) in the ones place, showing no ones
To create the Mayan number 40, they placed two ones in the 20’s place, and a zero below it:
 ← Two in the 20’s place = 2 × 20 = 40
← Two in the 20’s place = 2 × 20 = 40
 ← Zero (a shell) in the ones place, showing no ones
← Zero (a shell) in the ones place, showing no ones
Example 2 Convert 43 into Mayan.
The number 40 has two twenties in it, so, place two ones in the 20’s place, and three in the ones place below it:
 ← Two in the 20’s place = 2 × 20
← Two in the 20’s place = 2 × 20 ← Three in the ones place = 3 × 1
← Three in the ones place = 3 × 1 Generally, to create a Mayan number below 360, you need to figure out how many 20’s are in that number, and then what’s leftover after that.
Example 3 How did the Mayans write the number 100?
Caution! The number 100 was not written

 ← Zero in the ones place = 0 × 1 = 0
← Zero in the ones place = 0 × 1 = 0
(5 × 20) + (0 × 1) = 100 + 0 = 100
Computation note
There are many ways to figure out how many twenties you need. You could repeatedly add 20 until you get 100: 20 + 20 + 20 + 20 + 20 = 100
You could try multiplying 20 by various numbers until you find the one that gets you to 100: 10 × 5 = 100
Or you could divide: 100 ÷ 20 = 5
Any and all of these methods are fine. You will see the remaining examples shown with division, but when you work your own examples, you can use any or all of the above strategies.
Example 4 Convert 287 into Mayan.
To figure out how to convert the number 287 into Mayan, think of how many 20’s you would need first, then how many ones would be leftover. Since 287 ÷ 20 = 14.35, we will need 14 in the twenties place.
 ← Fourteen in the 20’s place = 14 × 20 = 280
← Fourteen in the 20’s place = 14 × 20 = 280 ← Seven in the ones place = 7 × 1 = 7
← Seven in the ones place = 7 × 1 = 7
Calculator note
If you are dividing on your calculator, the decimal does not directly tell you the remainder. For example, When I divide 287 ÷ 20 on the calculator, I get 14.35, but the remainder, what is left over after dividing, is not 35, it is 7.
To find the remainder, we must multiply the whole number part, then subtract: 287 ÷ 20 = 14.35, so multiply 14 x 20 = 280, then subtract: 287 – 280 = 7.
This procedure, or algorithm, has many steps, so can be complicated even for adults. If the procedure makes sense to you because you can “see” that 280 is “close” to 287, the steps become much easier to remember.
Writing Larger Numbers in Mayan
In a base ten system, the place values are the powers of ten:
| 100 | 101 | 102 | 103 | 104 | Etc. |
| 1 | 10 | 100 | 1,000 | 10,000 | |
| Ones | Tens | Hundreds | Thousands | Ten-thousands |
In a base twenty system, the place values are the powers of twenty:
| 200 | 201 | 202 | 203 | Etc. |
| 1 | 20 | 400 | 8,000 | |
| Ones | Twenties | Four-hundreds | Eight-thousands |
The Mayan number system used a modified base 20. Instead of 202 = 400, they used 360, because it was closer to the number of days in a year, which made calculations for their calendars easier. Thus, the place values were
The one’s place is one the bottom, and the place values go up from there.
Mayan place values:
| 200 | 201 | 360 | 360 × 20 | Etc. |
| 1 | 20 | 360 | 7,200 |
Caution: you may find on the internet that the Mayans used a pure base 20. This may have been true for the common people, but it was not what the priests used. The priests used a modified base 20 for their calendars and other calculations.
Example 5 Convert the number 392 into Mayan.
 ← 1 in the 360’s place, 1 × 360
← 1 in the 360’s place, 1 × 360 ← 1 in the 20’s place, 1 × 20
← 1 in the 20’s place, 1 × 20 ← 12 in the one’s place, 12 × 1
← 12 in the one’s place, 12 × 1
Example 6 Covert the number 803 into Mayan.
Think of how many 360’s you would need first, then how many twenties and ones you could make with what was left over. Since 803 ÷ 360 = 2.32…, we will need 2 in the 360’s place.
To figure out how much is leftover, 2 × 360 = 720, so we have 803 – 720 = 83 left to take care of using 20’s and ones.
 ← 2 in the 360’s place, 2 × 360 = 720
← 2 in the 360’s place, 2 × 360 = 720 ← 4 in the 20’s place, 4 × 20 = 80
← 4 in the 20’s place, 4 × 20 = 80 ← 3 in the one’s place, 3 × 1 = 3
← 3 in the one’s place, 3 × 1 = 3We end up with (2 × 360) + (4 × 20) + (3 × 1) = 803
Homework
Homework can be done in https://imathas.helpyourmath.com/ or on paper, below. Ask your instructor which you should be using.
Remember to show all your work and then to check your answers! But if your answer is different from the one in the answers, don’t just erase your answer. Instead, try to figure out why your answer is different — maybe it’s a totally legit different answer, or maybe you misunderstood something that you want to make note of and ask about in class discussion.