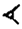Sec. 1.5 – The Babylonian Number System; Review of Converting between Bases
Chapter 1, Section 5
Math Topics – The Babylonian Number System; Review of Converting between Bases
Elementary Education – Deepening Our Understanding of Place Value
Babylonian Numbers
The Babylonians lived in Mesopotamia (modern day Iraq) about 1900 BC. Theirs “was an advanced civilisation building cities and supporting the people with irrigation systems, a legal system, administration, and even a postal service.” (From an article by J.J. O’Connor and E.F. Robertson, at the Math History website.)
The Babylonians formed their letters and numbers using a stylus (like a pen) pressed into clay, as shown below.

In the Babylonian number system, the symbol for 1 was a downward pointing triangle and the symbol for ten was a sideways wedge:
The symbol for 1
The symbol for ten
At first glance, the system may seem additive, because they created the numbers from 1 to 59 by combining the ones and tens symbols. For example, 36 was made with 3 tens and 6 ones:
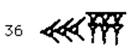
But the Babylonian system was actually a base 60, place value system, with place values of 600 = 1, 601 = 60, 602 = 3600, etc.
Example 1 Convert the number below to our system (Hindu Arabic).
|
|
|
|
| one in the 60’s place | 2 in the one’s place | |
| 1 × 60 | 2 × 1 | = 60 + 2 = 62 |
The space between the sets of symbols indicates that the first symbol for one is in a separate place value from the next two symbols. Since the system was base 60, this one was actually worth 60, similar to the way in which in the Hindu Arabic number 102, the 1 is actually worth 100.
Example 2 Convert the number 123 to Babylonian.
To make the number 123 in Babylonian, since 123 ÷ 60 = 2.05, we know there are two 60’s.
We know there are three left for the ones place because 2 × 60 = 120, and 123 – 120 = 3.
|
|
||
| two in the 60’s place | 3 in the one’s place | |
| 2 × 60 = 120 | 3 × 1 | = 120 + 3 = 123 |
Question: Now you try!
Example 3 Convert the number 683 to Babylonian.
We start by dividing: 683 ÷ 60 = 11.38333… Since the system was base 60, the Babylonians could have up to the number 59 in any given place value, so putting 11 in one place value was just fine! Since 11 × 60 = 660, there was 683 – 660 = 23 left for the ones place.
|
|
||
| 11 in the 60’s place | 23 in the one’s place | |
| 11 × 60 = 120 | 23 × 1 = 23 | = 660 + 23 = 683 |
Example 4 Convert the number 3,670 to Babylonian.
Now we have a number large enough to need the next place value – the 3,600’s place. The next place value is 3600 because the place values were powers of 60, and 602 = 3600.
If we place 1 in the 3,600 place, we have 3,600 – 3,670 = 70 left, which is one 60, plus 10 left over:
|
|
|||
| 1 in the 3600’s place | 1 in the 60’s place | 10 in the one’s place | |
| 1 × 3,600 = 3,600 | 1 × 60 = 60 | 10 × 1 = 10 | = 3,600 + 60 + 10 = 3,670 |
Question: Now you try!
The Babylonians Did Not Have a Symbol for Zero
There was one problem with the Babylonian number system – it did not have a symbol for zero. Because of this lack of a zero, the symbols for 3,601 would have looked the same as the symbols for 61. Both have a 1, then another 1, but 3601 would have a space in between. It would have been hard to tell if you had a space or not.
|
|
|
||
| 1 in the 3600’s place | 0 in the 60’s place | 11 in the one’s place | |
| 1 × 3,600 = 3,600 | 0 × 60 = 0 | 1 × 1 = 1 | = 3,600 + 0 + 11 = 3,601 |
|
[space]
|
|||
| 1 in the 3600’s place | 1 in the 60’s place | 0 in the one’s place | |
| 1 × 3,600 = 3,600 | 1 × 60 = 60 | 0 × 1 = 0 | = 3,600 + 60 + 0 = 3,060 |
This lack of a zero may seem as if it would have been a big problem. However, think about how much smaller a society must have existed then – around 40,000 people lived in their largest city, as opposed to over 8,500,000 people in New York City today.
With fewer people to keep track of, it is likely that the Babylonians were able to tell whether their neighbor had 61 “great cubits” of land or 3,601, or whether there were 61 goats next door or 3,601 goats, and so the lack of a zero may not have bothered them too much.
Converting Between Bases Review
The Babylonians number systems can help us review how to convert between bases. In example 1 we converted
into our system. This is like converting 1260 into base ten. We first make base 60 place values:
| 601 = 60 | 600 = 1 | |
| 1 x 60 | 2 x 1 | 60 + 2 = 62 |
When converting from Babylonian to base ten, we multiply by the base 60 place values.
Similarly, if we wanted to convert 2435 into base ten, we would start by making base 5 place values, and then multiply by those values:
| 52 = 25 | 51 = 5 | 50 = 1 | |
| 2 | 4 | 3 | |
| 2 × 25 = 50 | 4 × 5 = 20 | 3 × 1 = 3 | 50 + 20 + 3 = 73 |
We know we can place the base 5 number directly into the base 5 place values table because it is in base 5.
However, in example 2, to convert the number 123 to Babylonian, we did not multiply by the base 60 place values. Since 123 is not yet in Babylonian, we start with an empty base 60 table:
| 601 = 60 | 600 = 1 |
| ? | ? |
Converting 123 into Babylonian is done by converting 123 into base 60. We have to figure out how many 60’s and how many 1’s are in the number 123. We can do this by dividing: 123 ÷ 60 = 2, so we place 2 in the 60’s column and the remainder in the ones:
| 601 = 60 | 600 = 1 |
| 2 × 60 | 3 × 1 |
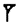
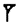
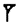
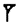
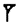 is like the number 2360 in base 60.
is like the number 2360 in base 60.Similarly, when if we wanted to convert 309 into base 6, we would start by making base 6 place values:
| 62 = 36 | 61 = 6 | 60 = 1 |
| ? | ? | ? |
But we do not place the 309 into this table because 309 is not a base 6 number. Instead, we divide by the place values (starting with the highest) to figure out how much we need in each place value:
309 ÷ 36 = 8.5833….
OOOPS! 8 is too high to put into one base 6 place values — remember, the highest you can place into a base 6 column is 5. So, let’s make one place value more in our table:
| 63 = 216 | 62 = 36 | 61 = 6 | 60 = 1 |
| ? | ? | ? | ? |
Now we start by dividing 309 by 216.
309 ÷ 216 = 1.4305…, so we place a 1 in the first place value.
| 63 = 216 | 62 = 36 | 61 = 6 | 60 = 1 |
| 1 | ? | ? | ? |
| 1 x 216 = 216 |
We have 309 – 216 = 93 left to place in the base 6 columns.
93 ÷ 36 = 2.583…., so we place a 2 in the next place value.
| 63 = 216 | 62 = 36 | 61 = 6 | 60 = 1 |
| 1 | 2 | ? | ? |
| 1 x 216 = 216 | 2 x 36 = 72 |
93 – 72 = 21 left to place in the base 6 columns. Divide 21 ÷ 6 to get 3, with 3 left.
| 63 = 216 | 62 = 36 | 61 = 6 | 60 = 1 |
| 1 | 2 | 3 | 3 |
| 1 x 216 = 216 | 2 x 36 = 72 | 3 x 6 = 18 | 3 x 1 = 3 |
216+72+18+3 = 309.
Thus, 309 = 12336.