Sec. 1.7 – Adding the Numbers from 1 to 100; Alternate Methods of Subtraction
Chapter 1, Section 7
Math Topics – Gauss’s Method of Adding the Numbers from 1 to 100; Alternate Methods of Subtraction
Elementary Education – Adding to Ten Facts; Mental Math
Adding to Ten Facts
The early grades are an important time for children to learn what adds to equal ten. They can model this addition using colored blocks, bundles of sticks, buttons, or other objects in the classroom.
Adding to Ten
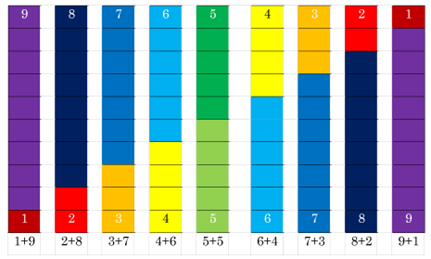
Children can use the adding to ten facts to add numbers by breaking them apart into what they know adds to ten.
Example 1 Add 8 + 5 using adding to ten facts and blocks.
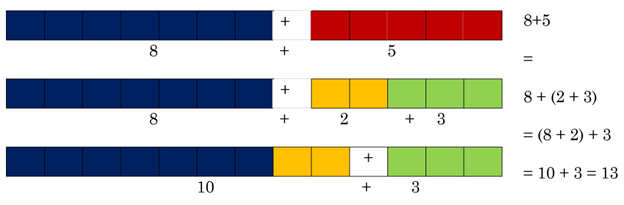
We can use the blocks to show that 8 + 5 is the same as 8 + (2 + 3), which can be regrouped as (8 + 2) + 3 = 10 + 3 = 13. This kind of breaking down and building up allows children to become better at mental math, that is, doing math in their head, which allows them to become more fluent in basic addition and subtraction.
The property that allows us to break down and regroup addition this way is called the associative property. That is, (a + b) + c = a + (b + c).
Example 2 Add 7 + 8 using adding to ten facts or another method you like. You can model it with objects, with lines, or with parenthesis.
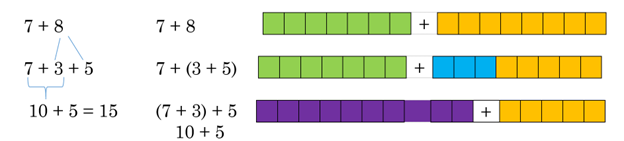
The image above shows breaking the 8 apart into 3 + 5, so that we get 7 + 8 = 7 + (3 + 5) = (7 + 3) + 5 = 10 + 5 = 15.
You might instead break apart the 7 into 5 + 2, which still uses adding to ten facts, to get 7 + 8 = (5 + 2) + 8 = 5 + (2 + 8) = 5 + 10 = 15. Or, if you know the “doubles” such as 4 + 4, 5 + 5, 6 + 6, etc., then you might think of 7 + 8 as 7 + (7 + 1) = (7 + 7) + 1 = 14 + 1 = 15, or even 8 + (8 – 1) = (8 + 8) – 1 = 16 – 1 = 15.
One way to get students to practice this type of breaking down and building up is to have each student explain to their group how they got an answer. Or students may be asked to write down how they got the answer. Of course, this can lead to some funny answers:

This is one of our favorites (even though it is from a website that is against common core math, and we think common core math is awesome). It can be very difficult to explain how you got an answer, so this kid has our sympathy! Still, explaining and talking out how you got the answer is an important thing to strive to be able to do.
Using Adding to Ten Facts and Other Groupings with Larger Numbers
In a previous section (1.3), we looked at partial sums addition, a method of addition that children can use after practicing with base ten blocks or alongside base ten blocks.
For example, students might add 456 + 375 by adding the hundreds, tens and one separately:
456 = 400 + 50 + 6
+ 375 = 300 + 70 + 5
700 + 120 +11 = 831
Students might also use their adding to ten facts to know when to trade in the ones place:
6 + 5 = 6 + (4 + 1) = (6 + 4) + 1, trade for one 10 with 1 left.
And students could use their adding to ten facts for higher place values as well: 50 + 70 = 50 + (50 + 20) = (50 + 50) + 20 – trade for one 100 with 20 left.
But this is not the only excellent way to break up the numbers to add them.
A student might also think of 456 + 375 as
(450 + 6) + (350 + 25)
= (450 + 350) + (6 + 25)
= 800 + 31 = 831
There are many other terrific ways to break down the two numbers to make them easier to add.
Try this a few different ways! There are many correct answers.
Gauss’s Method for Adding the Numbers from 1 to 100
Once upon a time, a teacher told a noisy, misbehaving class to add the numbers from 1 to 100 as a punishment. The teacher thought this would keep the children quiet for a long time. (Promise that you will never give out a math assignment to keep your class quiet!) But the legend goes that one child added the numbers together in only a few minutes, using a pattern he discovered. The child, Carl Friedrich Gauss (1777 – 1855), later became a famous mathematician.
What pattern did Gauss discover? Let’s look at a smaller, similar problem to see.
What if the problem were just to add the numbers from 1 to 10? How could you add these numbers easily, without adding in order, but instead using facts that children are supposed to learn?
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
Instead of adding 1+ 2 to get 3, then adding 3 to that, then 4 to that, young Carl might have thought about the adding to ten facts.
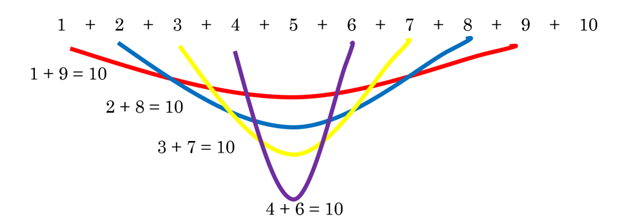
A drawback of this method is that it leaves a 5 in the middle. Is there a similar way to add that does not leave a middle number?
Perhaps he then tried this:
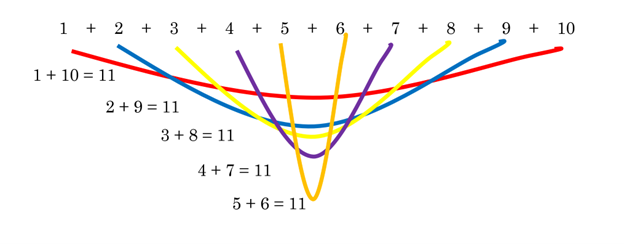
There are 5 pairs that each add up to 11.
5 × 11 = 55, so the numbers from 1 to 10 add up to 55.
Once we understand the smaller pattern, we can extend it to adding the numbers from 1 to 100, again adding the first and last number, the next number to the next to last, etc.
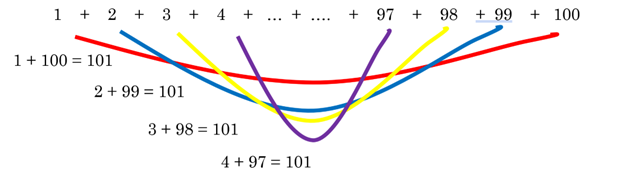
There are many more pairs, more than we can show in this picture.
How many pairs are there? Since there are 100 numbers from 1 to 100, there are 50 pairs. 50 pairs, each adding to 101, gives us a total of 50 × 101 = 5050. Thus, the numbers from 1 to 100 add up to 5050.
Example 3 Add the numbers from 1 to 30, using Gauss’s idea of adding the first and last number, etc.. How many added pairs would we have? What would the answer be?
We would be adding: 1 + 2 + 3 + 4 + … + 27 + 28 + 29 + 30. To add the first and last numbers, add 1 + 30. Next, add 2 + 29, 3 + 28, etc., each pair adding up to 31.
There are 30 numbers, so there would be 15 (half as many) pairs. 15 pairs that each add up to 31 would give you a total of 15 x 31 = 465.
Alternate Methods of Subtraction
In this part we share some alternative ways to subtract. These methods are mostly for you, not for your (future) students, but will help you guide your students better, including understanding why we should never say “We can’t subtract 7 from 3,” why children from other countries might come to your class with other subtraction methods, and the link to algebra!
In a previous homework, you were asked to try subtracting using partial sums subtraction using the problem 247 – 123.
Example 4 Subtract 247 – 123 using partial sums subtraction
This problem can be done in a similar way to partial sums addition:
| Subtract the 100’s then tens, then ones in your head | Or write the breakdown of each number into the place values, then subtract |
| 247 – 123 100 20 4 124 |
200 + 40 + 7 – (100 + 20 + 3) |
| distribute the subtraction: 200 + 40 + 7 – 100 – 20 – 3 100 + 20 + 4 = 124 |
Subtracting 247 – 123 using partial sums subtraction is similar to subtracting (2x2 + 4x + 7) – (x2 + 2x + 3)
The subtraction can be thought of as a negative sign that is distributed to each term in the parenthesis. Combining “like terms” is similar to adding or subtracting the place values that are the same:
| Subtract each place value | Subtract “like terms” |
| 200 + 40 + 7 – (100 + 20 + 3) |
2x2 + 4x + 7 – (1x2 + 2x + 3) |
| distribute the subtraction: 200 + 40 + 7 – 100 – 20 – 3 100 + 20 + 4 = 124 |
distribute the subtraction: 2x2 + 4x + 7 – 1x2 – 2x – 3 x2 + 2x + 4 |
Example 5 Subtract 621 – 153 using partial sums subtraction
In the homework challenge, we also asked you to try subtracting 621 – 153 using partial sums subtraction, which was much more difficult.
| Subtract the 100’s then tens, then ones | Or write the breakdown of each number into the place values, then subtract |
| 621 – 153 500 ?? ? |
600 + 20 + 1 – (100 + 50 + 3) |
| distribute the subtraction: 600 + 20 + 1 – 100 – 50 – 3 500 + ???? + ???? |
This problem is not quite as nice or intuitive as the previous problems. What do you do with 20 – 50? What about 1 – 3? Normally, you would “borrow,” or trade in this problem, so that you could avoid this difficulty. But if we wanted to try this using partial sums, without borrowing, what could we do?
Here, the connection to algebra can help us. A similar problem to 621 – 153 would be (6x2 + 2x + 1) – (x2 + 5x + 3). This problem is the same as 6x2 + 2x + 1 – x2 – 5x – 3 (after distributing the negative to each term), which we can also write like this:
6x2 + 2x + 1
– x2 – 5x – 3
Thing about what you would get for each term now.
6x2 + 2x + 1
– x2 – 5x – 3
5x2 – 3x – 2
Notice that we allow negative answers when we do the algebraic version. So why not allow negative answers with the numbers, too?
Negative Number Subtraction
In this type of subtraction, we use negative numbers whenever the number we are subtracting from is smaller than the number we are subtracting. For example, in the previous problem, since 20 is smaller than 50, we subtract 20 – 50 to get –30. Similarly, 1 – 3 also comes out to be a negative number, -2.
Example 5, continued Subtract 621–153 using negative numbers
| Subtract the 100’s then tens, then ones | Or write the breakdown of each number into the place values, then subtract |
| 621 – 153 500 -30 -2 468 |
600 + 20 + 1 – (100 + 50 + 3) |
| distribute the subtraction: 600 + 20 + 1 – 100 – 50 – 3 500 – 30 – 2 = 468 |
Again, as with partial sums addition, this can be done in any order, from left to right or right to left, taking any place value first.
Example 6 Subtract 52 – 29 using negative numbers
| Subtract the tens, then ones | Or write the breakdown of each number into the place values, then subtract |
| 52 – 29 30 -7 23 |
50 + 2 – (20 + 9) |
| distribute the subtraction: 50 + 2 – 20 – 9 30 – 7 = 23 |
From this example, we can see why, when subtracting with your students, it is wise to avoid saying, “You can’t subtract 9 from 2,” because of course, you can subtract 9 from 2 if you allow negative number answers, and even some of your younger students may know negative numbers.
Question Now you try!
Front-end (Mexican) subtraction
Students of ours remember using this as children in Mexico. One author’s mother also learned a variation of this as a child in Germany. Here, we work from left to right instead of right to left, and we borrow from our answer instead of from the numbers in the problem.
Example 7 Subtract 54 – 29 using front-end subtraction
| Step 1: Subtract the tens
54 -29 3 |
Step 2: look at the ones place and realize you have to borrow | Step 3: Borrow from the answer of 3
5 -29
2 5 |
Example 8 Subtract 314 – 138 using front end subtraction
For three digits, again work from left to right instead of right to left.
| Step 1: Subtract the hundreds
314 -138 2 |
Step 2: look at the tens place and realize you have to borrow | Step 3: Borrow from the answer of 2
3 -138
18 |
Step 4: Repeat with the ones place
31 -138
1 7 6 |
Equal Addition Subtraction
Another fun method to try is called equal addition subtraction. It uses the “adding to ten facts” but I would not share it with children except maybe as a fun extension for advanced students.
Equal addition subtraction works because if you add or subtract the same value to both the number you start with and the number you are subtracting, you have an equivalent problem. So, you can add whatever you like to make it a “nicer” problem! One way to make your nicer numbers to subtract is to use the “adding to ten” facts.
Example 9 Subtract 52 – 29 by making 29 into an easier number to subtract.
| 52 +1
–29 +1 |
53
–30 |
30 is an easier number to subtract than 29. |
| 23 | 23 |
Example 10 Subtract 305 – 168 by making 168 into an easier number to subtract.
| 305 + 42
–168 + 42 |
347
–210 |
210 is an easier number to subtract than 168. |
| 137 | 137 |
We could also have added 32 instead, since 168 + 32 = 200, and 200 is also easier to subtract than 168.
The first purely uses the adding to ten facts, the second uses the fact that adding 32 is enough because of trading 10 for one in the next place value. There are many ways to get a “nicer” number on the bottom. You can even subtract from both numbers. The key is that you should not have to do any “borrowing” when you subtract your two new numbers.
Question Now you try!
Note
This technique is similar to what happens when you buy a product for $1.02, and you have $2, which would be the subtraction $2 – 1.02, which results in $.98 worth of change (Ugh!)

$2.00 – $1.02 = $.98, ugh!
So, you say, “Oh, I have 2 cents,” which changes the problem into $2.02 – $1.02 = $1, a much nicer result – but note that here you are changing the problem and changing the answer. So this is not quite the same as equal addition subtraction, where the answer stays the same.

$2.02 – $1.02 = $1.00, much nicer!