Chapter 2, Section 1

Math Topics – The Sieve of Eratosthenes, Prime Numbers, Goldbach’s Conjecture, Mersenne Primes

Elementary Education – Multiples, Divisibility Rules and Patterns

In chapter 1, we saw how children even as young as pre-K can use skip counting, objects, and base ten patterns. For older children, the table of numbers from 1 to 100 can be a great tool to explore patterns.

1 to 100 table

Children can color in numbers in the table to see skip-counting patterns, and gradually begin to talk about multiples of numbers.

Definition. A multiple of a number is what we get when we multiply an integer by that number. For example, 21 is a multiple of 3, since 7 × 3 = 21.

For example, if we multiply 3 multiplied by the integers …-4, -3, -2, -1, 0, 1, 2, 3, 4, etc., we get that the multiples of 3 are …-12, -9, -6, -3, 0, 3, 6, 9, 12 …

A multiple of a number is divisible by that number. For example, the multiples of 3 are divisible by 3. This means that 3 divides into the number without a remainder.

Definition. A factor of a number divides into that number evenly (without a remainder). For example, 3 is a factor of 21, since 21 ÷ 3 = 7, with no a remainder or decimal.

How to Tell if a Number is a Multiple of 2

Try skip-counting by 2’s. This is a way to find the multiples of 2. What pattern do you see? 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, ….

Color in the table to see the pattern more clearly.

1 to 100 table, showing multiples of 2

The multiples of 2 always end in 0, 2, 4, 6, or 8. Thus, a number is divisible by 2 if it ends in 0, 2, 4, 6, or 8. Another way to say this is that multiples of 2 always end in an even number. Notice that 100 is divisible by 2, since it ends in a zero. We can also say 2 is a factor of 100.

How to Tell if a Number is a Multiple of 3

Try skip-counting by 3’s. What pattern do you see? Do the multiples of 3 also have a special set of end digits?

The table shows an interesting diagonal pattern that means the digits do not always end in the same number. If we look at 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, …., we see that the multiples of 3 end in every possible digit from 0 to 9, so the ending number will not tell us if we have a multiple of 3.

But if we add the digits together, a pattern emerges:

12, 15, 18, 21, 24, 27,  …

A number is a multiple of 3 if its digits add up to a multiple of 3.

Notice that 84 is divisible by 3, since 8 + 4 = 12, which is a multiple of 3. We can also say 3 is a factor of 84.

Example 1 Use divisibility rules to decide whether 2421 is divisible by 2 or by 3.

2421 is not divisible by 2 because it ends in a 1, which is not is not 2, 4, 6, 8 or 0.

For 3, add up the digits: 2+4+2+1 = 9, so 2421 is divisible by 3 because the digits add up to 9, which is a multiple of 3.

3 is a factor of 2421, but 2 is not a factor of 2421.

How to Tell if a Number is a Multiple of 5

Is the rule for multiples of 5 similar to the rule for multiples of 2, or to the rule for multiples of 3? Again, we can try skip counting or coloring in the table to see:

The rule for multiples of 5 is similar to the rule for multiples of 2, in that, for a number to be divisible by 5, it must end in 0 or 5. For example, 100 is a multiple of 5, since it ends in 0. We can also say that 5 is a factor of 100.

Example 2 Use divisibility rules to decide whether 5253 is divisible by 5.

5253 is not divisible by 5 because it ends in a 3, which is not is not 5, or 0. Notice that if we add up the digits, 5+2+5+3, we get 15, which is a multiple of 5, but that is not the correct rule/pattern, so it does not give us the correct conclusion.

How to Tell if a Number is a Multiple of 6

If you color the multiples of 2 in the table yellow and the multiples of 3 in the table blue, what kinds of multiples end up being colored with both colors, so that they end up green?

The numbers that end up green are the multiples of 6, because we colored them in yellow (multiples of 2) and blue (multiples of 3). For a number to be divisible by 6, it must be divisible by 2 and by 3.

Example 3 Use divisibility rules to decide whether 2421 is divisible by 6.

2421 is not divisible by 6 because although it is divisible by 3, it is not divisible by 2, and it must be divisible by both 2 and 3 to be divisible by 6.

The Original Bizz Buzz — for Multiples

The original game, Bizz Buzz, is a game for multiples.You can play it with any two multiples. For example, if you play it for 2 and 3, you count normally, except that if you are on a multiple of 2, then you say bizz instead of that number. If you are on a multiple of 3, then you say buzz instead of that number. The people who get the multiples of both say bizz buzz!

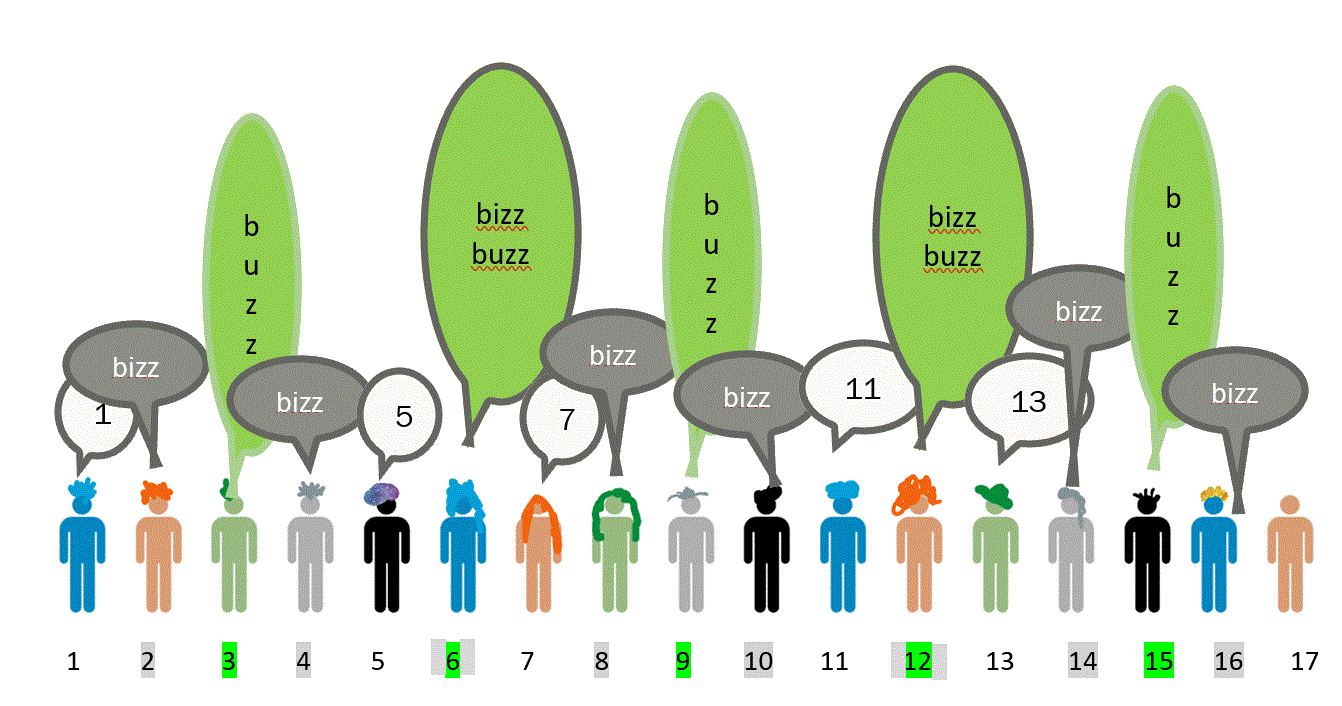
Counting Bizz Buzz for multiples of 2 and 3, the class would count, “1, bizz (instead of saying 2), buzz (instead of saying 3), bizz (instead of 4), 5, bizz-buzz (instead of 6), 7, bizz, buzz, 11 …”

Notice that the numbers where you say bizz-buzz are the numbers that are multiples of 2 and 3. So you would say bizz-buzz for 6, for 12, …. and for….?

The next one where you would say bizz buzz would be 18. The numbers where you say bizz buzz are the multiples of 6!

Bizz Buzz is a great way for students to see common multiples, which also helps them work with fractions.

How to Tell if a Number is a Multiple of 9

The rule for multiples of 9 is similar to the rule for multiples of 3. For a number to be divisible by 9, the digits must add up to a multiple of 9.

Example 4 Use divisibility rules to decide whether 1140 is divisible by 9 or by 5.

Add up the digits: 1+1+4+0 = 6. Since 6 is not a multiple of 9, 1140 is not divisible by 9. Since the number ends in 0, it is divisible by 5, because the multiples of 5 end in 5 or 0.

Example 5 Is 1140 is divisible by 45? Use divisibility rules to decide.

45 = 9 × 5, so for a number to be divisible by 45, it must be divisible by 9 and by 5. Since 1140 is not divisible by 9, it is not divisible by 45.

The Pattern of Nines

In addition to the fact that the two integers always as up to 9, you can also see that the tens place goes up (blue arrow), while the ones place goes down (green arrow).

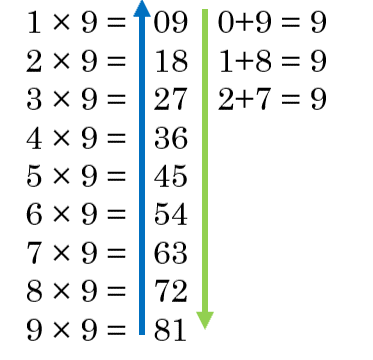
In addition to looking down from the previous answer to get the next answer, we can look across from the two multiples to see a pattern that relates the two multiples to the answer. For example, look at 3 x 9 = 27. How is the multiple, 3, related to the tens place of the answer? Look at 4 x 9 = 36. How is the multiple, 4, related to the tens place of that answer?

The pattern is that the tens place is always one less than the multiple. For example, for 4 × 9, the tens place in the answer is 3, one less than 4:

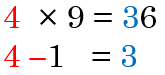
We also know that the two digits must add up to 9. Thus, to figure out the answer to 4 × 9, we can subtract 1 from the 4, which is 3, then figure out how much more we need to get to 9. Since 3+6 = 9, the ones place must be 6.

Example 6 Find 7 × 9 using the pattern of 9’s.

Subtract 1 from 7 to get the tens place: 7 – 1 = 6, so the tens place is 6. Then we know 6 + 3 = 9, so the ones place must be 3. 7 × 9 = 63.

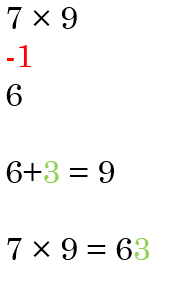
We can show the same idea with our fingers – bend down the 7^th finger – this subtracts 1 from it. since the finger is bent down (taken away). The remaining fingers add up to 9!

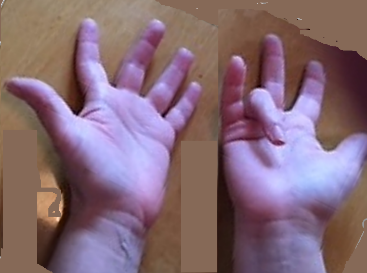
For 7 × 9, bend down the 7^th finger. Now you have 6 fingers and 3 fingers = 63.

Question: Now you try! Is 378 divisible by 6? By 9? Give the correct rule for how you can tell. https://koffenholley.survey.fm/is-378-divisible-by-6-by-9

The Sieve of Eratosthenes

• Circle the number 2, then cross out all multiples of 2.
• Circle the next number, 3, then cross out all multiples of 3.
• Circle the next number that has not been crossed out (5), and cross out all multiples of 5.
• Continue in this way until all the numbers have been crossed out or circled.

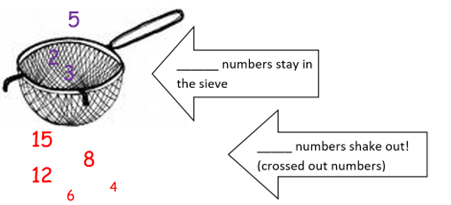
Try this yourself using a printout of the table, above, or go to https://www.visnos.com/demos/sieve-of-eratosthenes to use the applet! What do the numbers you are circling have in common? What kinds of numbers get crossed out?

The types of numbers that you circled are called prime numbers. The numbers you crossed out are called composite numbers.

The sieve was invented by Eratosthenes over 2000 years ago to “catch” prime numbers. Eratosthenes was a mathematician, music theorist, astronomer, geographer and poet. He was the first person to calculate the circumference of the earth.

Definition of Prime: Informally, a prime is a number that cannot be divided by more than just itself and one. For example, 13 is prime because it can only be divided by 1 and 13. But the formal definition of prime is slightly different. Formally, a prime is a number that has exactly two factors. For example, 13 is prime because it has exactly two factors, 1 and 13. You will see that the formal definition matters when it comes to deciding whether or not the number 1 is prime.

Definition of composite: a composite number has more than two factors. For example, 15 is composite because the factors of 15 are 1, 3, 5, and 15.

Example 7 Is the number 55 prime or composite?

55 is composite because it has more than 2 factors. The factors are 1, 5, 11 and 55.

Example 8 Is the number 1 prime or composite?

1 is neither prime nor composite! 1 only has one factor, itself, so it does not fit into the definition of either prime or composite.

The prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, …

Goldbach’s conjecture

Christian Goldbach was a Russian mathematician who proposed the conjecture in 1742, that every even integer greater than 2 can be written as the sum of two primes. To figure out what he meant, read the conjecture very slowly, and think about how to translate each part:

Every even integer →the even integers are …-4, -2, 0, 2, 4, 6, 8

greater than 2→so we want 4, 6, 8, ….(even integers bigger than 2)

can be written as →=

the sum of →add

two primes.→two numbers from the list of primes, above

Put these translations together and we get

4, 6, 8, … = prime + prime

For example: 8 = 3 + 5

(8 is an even integer greater than 2 and it can be written as the sum of two primes, 3 and 5).

Example 9 Show that Goldbach’s conjecture is true for the number 10. Then show that it is true for some other greater even number of your choice.

10 = 7 + 3 or 10 = 5 + 5 (it is okay to use the same prime twice). For a greater even integer, you could pick 12, which is 12 = 5 + 7, or 14, which is 14 = 3 + 11 or 7 + 7, or you might pick a different even integer.

A conjecture means an educated guess! Even though many even numbers have been found to be the sum of two primes, nobody has yet proven that this will always work for any even number.

A Mersenne number, named after Martin Mersenne (a French monk who began the study of these numbers in the early 17^th century), is a positive integer that is one less than a power of two:

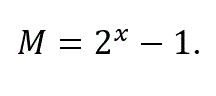
For example, if x = 3, we get

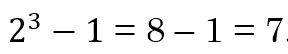
Notice that both the x value, 3, and the answer, 7, are prime numbers.

A Mersenne prime is a Mersenne number that is prime. Complete the table below to figure out which Mersenne numbers are prime.

Question: If let x = 5 in the Mersenne number formula, is the result prime or composite? What about if x = 6? https://koffenholley.survey.fm/mersenne

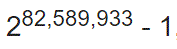
As of 2018, 51 Mersenne primes were known, including the largest known prime number, which over 24 million digits long!

Example 10 Use the formula to find the Mersenne number when x = 8. Is this number a Mersenne prime?

When x = 8, we get 256-1=255. This number is not prime, since it is divisible by 5. Also note, 8 is not a prime number. If we use a value for x that is not prime, we do not get a prime number result!

Example 11 Use the formula to find the Mersenne number when x = 11. Is this number a Mersenne prime?

When x = 11, we get 2048-1=2047. This number looks like it is prime, and we can use divisibility rules to see that it is not divisible by 2, 3 or 5. But maybe it is divisible by a higher number. Keep checking!

Tips to see if a number is prime:

• You only have to check if the number is divisible by primes (because if it is not divisible by a prime, it will not be divisible by a composite number that is made up of that prime). So, on your calculator, check if 2047 ÷ 7 works (divides without a remainder) then check 2047 ÷ 11, 2047 ÷ 13, etc.
• You can stop checking once your answer (the quotient) comes out smaller than the numbers you have checked (the divisors).

2047 is not a prime, since it is divisible by 23 and 89.

To get a Mersenne prime, x (the exponent) must be prime. But just because x is prime does not guarantee that the resulting number will always be prime.

Summary of the Divisibility Rules you Must Know for this Class

2 A number is divisible by 2 if it ends in an even number — 0,2, 4, 6, or 8. Example 1: the number 236 is divisible by 2 because it ends in 6, which is an even number. Example 2: the number 231 is not divisible by 2 because it ends in 1, which is not an even number.

3 A number is divisible by 3 if the digits in the number add up to a multiple of 3. Example 1: the number 231 is divisible by 3 because 2+3+1 = 6, which is a multiple of 3. Example 2: The number 233 is not divisible by 3 because 2+3+3 = 8, which is not a multiple of 3. Caution: even if a number ends in 3, it might not be a multiple of 3.

5 A number is divisible by 5 if it ends in 5 or 0. Example 1: the number 110 is divisible by 5 because it ends in 0. Example 2: the number 551 is not divisible by 5 because it ends in 1, which is not a 5 or a 0.

6 A number is divisible by 6 if it is divisible by 2 and by 3. Example 1: the number 234 is divisible by 6 because 2+3+4 = 9, so it is divisible by 3, and it ends in and even number, so it is divisible by 2. Example 2: the number 231 is not divisible by 6 because it is divisible by 3, but it is not divisible by 2, because it does not end in an even number.

9 A number is divisible by 3 if the digits in the number add up to a multiple of 9. Example 1: the number 231 is not divisible by 9 because 2+3+1 = 6, which is not a multiple of 9. Example 2: The number 531 is a multiple of 9 because 5+3+1 = 9, which is a multiple of 9.

Caution: two of these rules are about what the number ends in, and two are about adding up the digits. You can’t use adding up the digits for everything, and you can’t use what the number ends in for everything! Remember the patterns you found!