Sec. 2.3 – Problem Solving Strategies for All Ages
Chapter 2, Section 3
Math Topics – Problem Solving Strategies
Elementary Education – Estimation, Problem Solving
Problem Solving Strategies
In 1945, mathematician George Polya published a small book titled How to Solve It. It has since been translated into many languages and has sold over a million copies. I have a copy of it in my office.
One of the best things about this book is that it offers general problem-solving strategies that can be used on any kind of math problem, whether you are solving a geometry problem, like the one on the cover of his book, or a problem about Goldbach’s conjecture, as you did in the previous section.
To solve a math problem, Polya gives the following four steps (as reworded by the authors):
- First, work to understand the problem.
- Next, make a plan for what strategies you are going to use. These strategies include to
-
-
- create a table of the information, or a list
- create a similar, smaller problem to try first
- look for a pattern
- guess/estimate and check (also called trial and error)
- work backwards
- draw a picture or make a physical model
- describe and solve the problem algebraically
-
- Carry out the plan you decided on in step 2.
- Look back on your work. Does your answer make sense? Do you need to try a new plan?
We already practiced step one in section 2.1, when we translated Goldbach’s conjecture into our own words. Part of understanding the problem can include reading the problem again more slowly and rewording the problem. In example 1, below, we practice that skill again on a new problem.
Example 1 There is a conjecture, similar to Goldbach’s conjecture, that every multiple of 6 can be written as the difference of two primes. Show an example.
Step 1: Understand the problem.
Every multiple of 6 → What are the multiples of 6? Make a list!
can be written as → Which symbol is “can be written as”? Here are some possible answers: +, -, ×, ÷, = . Which one is correct?
the difference → Which symbol is “difference”? Here are some possible answers: +, -, ×, ÷, = . Which one is correct?
of two primes. → What are the prime numbers? Make a list!
Try translating this yourself before you continue. Don’t scroll down until you try!
Every multiple of 6 → The multiples of 6 are ….-12, -6, 0, 6, 12 …
can be written as → =
the difference → The word difference means to subtract, -.
of two primes. → The primes are 2, 3, 5, 7, 11, 13, 17, …
Thus, we want a multiple of 6 equal to a prime number minus a prime number.
__________ = ______ – _______
multiple of 6 = prime – prime
Steps 2 and 3: Now that you understand the problem, see if you can find two primes that, when you subtract them, give you 6, or another multiple of 6. This is the guess and check strategy.
An example might be 6 = 11 – 5, or 12 = 17 – 5, or you may have thought of a different multiple of 6.
Try your own new multiple of 6!
Notice that when we solved this, in addition to guess and check, we also made use of the first of the problem-solving strategies – we made lists of the multiples of 6 and of the primes.
Question: Now you try!
Which of these is an example of the above conjecture?
12 = 1+11 ?
18 = 21 – 3 ? 24 = 29 – 5 ?
What about 21 = 23 – 2?
TIP: for each of these, do we have a multiple of 6 equal to the difference of two primes? Check your answer, here.
Now let’s try some problems that would work best using other strategies in step 2.
Example 2 Find the ones digit of 2400.
Step 1: Understand the problem. What does the “ones digit” mean? It’s the last digit. So we are trying to find out, if we raised 2 to the 400 power, what digit (number) that answer would end in.
If you try to find 2400 on your calculator, you may get an error because the exponent is so large. Or you may get something like 2.58… E120. E120 does not indicate an error; instead, it means 10 to the 120th power. Your calculator has rounded off the answer and is telling you that it’s approximately 2.58 x 10120. The last digit you see on your calculator display is not the real last digit, because the actual number is 121 digits long! So we will have to figure out another way, besides using a calculator, to find the ones place of 2400.
Before we continue this problem, see if you can choose which of these might be good problem solving strategies to use on this problem, without scrolling below to check: looking for a pattern, multiplying by 2, creating a table, trying a smaller problem.
— spoiler space —
don’t scroll down yet!
Steps 2 and 3: Let’s try the problem solving strategy of creating a similar, smaller problem to try first. Let’s try looking at smaller powers of 2.
21 = ____
22 = ____
23 = ____
24 = ____
25 = ____
26 = ____
27 = ____
28 = ____
Before you continue reading, fill in the powers, above.
Step 4: Think about how your plan is going so far. Do you need to use another problem solving strategy? Go back to the top of the page and see if the third strategy on the list might help. You may also want to organize your results into a list or table (the first strategy).
The powers of 2 are:
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
There is a pattern in the ones digits: 2, 4, 8, 6, 2, 4, 8, 6…. It might help to organize the results into a table that shows that pattern more clearly.
| 21 = 2 | 25 = 32 | 29 = …2 | 213 ends in 2 |
| 22 = 4 | 26 = 64 | 210 = …4 | 214 ends in 4 |
| 23 = 8 | 27 = 128 | 211 = …8 | 215 ends in 8 |
| 24 = 16 | 28 = 246 | 212 = …6 | 216 ends in 6 |
Each answer ends in a ones digit of either 2, 4, 8 or 6, then it repeats again after every fourth answer.
If we look at the fourth entries, we see 24, 28, 212, etc. What kinds of numbers are these?
They start at 4 and skip every 4 or we could say they add 4 each time. So they are all multiples of 4.
Where would 2400 go on this table? How do you know?
2400 would be here in the last row, because 400 is divisible by 4.
| 2397 = …2 | 2401 ends in 2 |
| 2398 = …4 | 2402 ends in 4 |
| 2399 = …8 | 2403 ends in 8 |
| 2400 = …6 | 2404 ends in 6 |
All the powers that are divisible by 4 are in this last row. This means that the answer to 2400 would end in a 6.
We can extend the idea to ask what 2403 would end in. 403 is not divisible by 4, but it is close to a number that is divisible by 4. We know where 2400 would go in the table, so we can count 3 more rows in the table from there to where the 403rd power would go.
Thus, 2403 would end in an 8.
Another way to think of this is to divide 403 by 4, since the pattern goes by fours. The remainder of 403 ÷ 4 is 3, so 403 would end up in the third row. Numbers in the 3rd row always end in 8, so our answer would end in an 8. The 100 means there are 100 sets of 4, then three more numbers after that, to make 403.
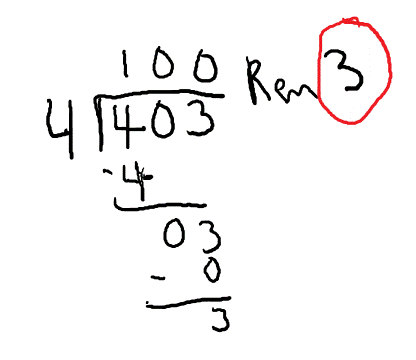
Caution: there are other ways to extend from a smaller problem to a bigger one that do not work. For example, I might look at the pattern and decide that since 23 =8, if I extend that by multiplying by 10, 230 will also end in 8. But it will not, it will end in a 4. You can actually try this one on your calculator to see: 230 = 1,073,741,824, so it ends in a 4. You need to have a good reason for the way you extend your smaller problem to the bigger one. Multiplying by 10 does not work here. You can test out your conjecture of how to extend the smaller problem to the larger problem by first trying out a slightly bigger one.
Example 3 Find the 99th and 100th letters in the sequence CATCATCATCAT…

Again, let’s try the problem-solving strategy of looking for a pattern.
We can see that the letters repeat themselves, and that the repeating pattern is three long. The third letter is a T, the 6th letter is again a T, then the 9th letter is a T.
As in the previous problem, it might help to organize our pattern into a table.
| 1 C | 4 C | 7 C | 10 C | 13 C |
| 2 A | 5 A | 8 A | 11 A | 14 A |
| 3 T | 6 T | 9 T | 12 T | 15 C |
What pattern do you notice in the numbers that correspond with where the letter T ends up?
3, 6, 9, 12, 15, ….
These are all multiples of 3.
Since 99 is also a multiple of 3, the 99th letter will also be a T.
| 1 C | 4 C | 7 C | 10 C | 13 C | ||||
| 2 A | 5 A | 8 A | 11 A | 14 A | ||||
| 3 T | 6 T | 9 T | 12 T | 15 T | … | … | 99 T |
Since the 100th letter is just one more than the 99th, the 100th letter will start at at C again.
| 1 C | 4 C | 7 C | 10 C | 13 C | 100 C | |||
| 2 A | 5 A | 8 A | 11 A | 14 A | ||||
| 3 T | 6 T | 9 T | 12 T | 15 T | … | … | 99 T |
Note: it may be tempting to look at the letter C in the pattern, instead of the T. For example, maybe you would guess that if the 10th letter is a C, then the 100th letter will also be a C, and that is true – but that was just a lucky guess! The letter C doesn’t have a consistent pattern to it – for example, the 4th letter is a C, but the 44th letter is an A. The 10th letter is a C, but the 30th letter is a T. To reason using a pattern, make sure you use a consistent pattern. We do see a consistent pattern of multiples of three for the letter T, so that’s the letter to use!
Question: Now you try!
In the pattern CATCATCATCAT… what is the 116th letter? Why? Check your ideas, here.
In the pattern … what is the 100th number? Why?
Example 4 Augustus DeMorgan was a mathematician who lived in the 19th century. He said, “I was x years old in the year x2.” When was he born?
Step 1: Understand the problem.
He lived in the 19th century → he lived in the 1800’s
He said, “I was x years old→ we want some number for his age
in the year x2.”→ and we want to square it and get a year
Step 2: What strategy should we use? It looks like we should use algebra, since there is an x and an x2, but we have x = some age and x2 = some year, which is not specific enough for algebra.
We should try another strategy. Maybe guess and check?
Try 10… 102 = 100… so he was 10 years old in the year 100?
Should our next try be higher or lower than 10? Teacher’s tip: when kids are told to guess and check, they don’t really understand the “check” part at first. You might see that they guess wildly, and don’t base their guesses on any estimation. It’s very important to teach your students how to guess in a strategic way, then how to check and change their guess based on new evidence. So you will probably have to teach them that if their answer comes out way too low, their next guess should be higher.
Back to our problem….
Try higher, maybe 30? … 302 = 900 … so he was 30 years old in year 900?
This is starting to look better, but didn’t he live in the 1800’s?
Guess strategically: try other numbers that get closer to the 1800’s.
You should find that he was 43 in 1849. This is the only answer that works.
But we didn’t answer the question yet! He was born in ….?
1849 – 43 = 1806.
Augustus DeMorgan was born in 1806. In 1849, he was 43 years old.
Example 5 A man goes to the track each week to bet on horses. The first week, he triples his money, but then loses $12. He saves what he now has, to play the next week. The next week, he takes his money back, doubles it, but then loses $40. The following week, he tries again, and quadruples his money! He decides this is a great time to quit betting, and keeps the $224 he has won. How much money did the man start with?
Step 1: understand the problem.
The man started out with some money →
and triples it →
then loses $12 →
He takes his money back, doubles it →
but then loses $40 →
quadruples his money →
keeps the $224 he has won →
The man started out with some money → some number
and triples it → three times that number
then loses $12 → subtract 12 from the result
He takes his money back, doubles it → two times the previous result
but then loses $40 → subtract 40 from the result
quadruples his money → multiply the previous result by 4
keeps the $224 he has won → the final number is 224
Step 2: pick a problem solving strategy to try. This looks like a job for algebra!

Let’s try it. Start with x, then triple it: 3x,
The man started out with some money → x
and triples it → 3x
then loses $12 →
so subtract 12 from that result: 3x – 12. Pretty good so far.
He takes his money back, doubles it → two times the previous result: 2(3x – 12)
but then loses $40 → subtract 40 from the result
(3x – 12) – 40
This looks a little complicated.
quadruples his money → multiply the previous result by 4:
4(2(3x – 12) – 40)
and keeps the $224 he has won → the final number is 224:
4(2(3x – 12) – 40) = 224
Yikes! This is solvable, but another method might be easier. Remember that Polya’s step 4 involves looking at how your problem solving is going, and choosing a new one if needed.
Step 3 redo: let’s try the strategy of working backwards instead.
Start with the final number, 224. Right before that, he had quadrupled his money.
quadruples his money → multiply the previous result by 4
If we instead divide by 4, we will get what he had before he had $224.
224 ÷ 4 = 56, so he had $56 before he quadrupled (multiplied by 4) his money.
but then loses $40 → subtract 40 from the result
So he had some amount of money that he subtracted 40 from, to get the $56.
If we instead add 40, we’ll get the previous amount:
56+40 = 96 He had $96 before he subtracted 40, because 96 – 40 = 56.
We are working backwards and doing the opposite at each step. Try to complete this on your own before reading the next part, starting at the bottom.
| The man started out with some money → some number
and triples it → three times that number then loses $12 → subtract 12 from the result He takes his money back, doubles it → two times the previous result but then loses $40 → subtract 40 from the result quadruples his money → multiply the previous result by 4 keeps the $224 he has won → the final number is 224 |
7. ?
6. ? 5. ? 4. ? 3. Add 40 = 56 + 40 = 96 2. Divide 224 by 4 = 56 1. Start here at 224 and go up (backwards)! |
Start at the bottom and work your way up by working backwards! Steps 1, 2, and 3 are written in for you. See if you can figure out step 4 by working backwards and doing the opposite.
Hint: think of the opposite of doubling, the opposite of multiplying by 2.
Then try to figure out step 5. Use the table, above, to remind you of what to get the opposite of.
Keep going! See if you can get all the way backwards to step 7.
| The man started out with some money → some number
and triples it → three times that number then loses $12 → subtract 12 from the result He takes his money back, doubles it → two times the previous result but then loses $40 → subtract 40 from the result quadruples his money → multiply the previous result by 4 keeps the $224 he has won → the final number is 224 |
7. 20
6. Divide the previous answer by 3: 60 ÷ 3 = 20 5. Add 12 to your previous answer: 48 + 12 = 60 4. Divide your previous answer (from step 3) by 2: 96 ÷ 2 = 48 3. Add 40 = 56 + 40 = 96 2. Divide 224 by 4 = 56 1. Start here at 224. |
Finally, do the last step in Polya’s list: look back on your work. Test your answer out going forward. Does it work?
| The man started out with some money → some number
and triples it → three times that number then loses $12 → subtract 12 from the result He takes his money back, doubles it → two times the previous result but then loses $40 → subtract 40 from the result quadruples his money → multiply the previous result by 4 keeps the $224 he has won → the final number is 224 |
1. Start here! 20
2. 20 × 3 = 60 3. 60 – 12 = 48 4. 48 × 2 = 96 5. 96 – 40 = 56 6. 56 × 4 = 224 7. He keeps $224. |
Let’s look back at our algebraic equation, 4((3x – 12) – 40) = 224
The steps we would use to solve it are the same as what we used when we worked backwards!
4(2(3x - 12) - 40) = 224
÷4 ÷4
2(3x - 12) - 40 = 56
+40 +40
2(3x - 12) = 96
First, divide both sides of the equation by 4 to get rid of the 4 multiplying everything:
Next, add 40 to both sides.
See if you can continue the solution to get x, the amount he started with.
The strategy of working backwards is a skill that helps children with the skills they will need when they learn algebra. It is part of what is called pre-algebraic reasoning.
Question: Now you try!
Test your vocabulary and understanding: what does double mean? What is the opposite of doubling? What does triple mean? Quadruple? What are their opposites? What is the opposite of cutting in half? Check your ideas, here.
Now use working backwards to find the answer: — new problem
Example 6 Estimation
Estimation is part of the problem strategy of guess and check. Just as you teach kids to use an educated guess instead of a wild guess, you can teach kids to estimate by benchmarking. Benchmarking means to figure out the whole amount by first figuring out a small part, then seeing how many of that part are in the whole.
For the picture below, we can use benchmarking to estimate the approximate total number of pink flowers.

It looks like there are roughly 80 pink flowers per large petal, and there 9 petals, so that would make 9 x 80 = 720 pink flowers. But opinions differ on what’s one pink flower, and how many there are per petal, so there is no one correct answer!
In your own classroom, you could challenge kids to figure out how many objects are in a whole jar of jelly beans by figuring out how many are in a part of the jar, then they multiply that by the number of parts they think there are in the jar.
The next-to-last problem solving strategy on the list is to draw a picture or make a physical model. We have already been using this strategy in our class in many ways. Think of the base ten and base five blocks we played with and the pictures of trading we made. In addition to using base ten blocks, children can make patterns using regular wooden blocks, Unifix cubes, or, as we have seen in the past videos, any kind of object!
Finally, the last strategy on the list is to describe and solve the problem using algebra or algebraic reasoning. You have been doing this for years in your math classes, so it is left for last here, since it is probably a strategy that is familiar to you. But it’s time to look at the strategy in a new way, for how you can work on this skill with your students.
Example 7 The pattern of multiples of 11
Do you remember the pattern of 9’s from the previous section? That pattern involved pre-algebraic reasoning — looking at a pattern to see that the same sort of thing happens each time, to help us get the answer. Let’s see if you can try a similar idea, here, with the pattern of 11’s.
You may already know that for the first multiples of 11, we always get double digits: 5 x 11 = 55, 6 x 11 = 66, 7 x 11 = 77. Notice that the multiple is the same as the number we get for our double digits.
7 × 11 = 77
↑ the same ↑
But after 10 x 11, a different pattern emerges
121
132
143
154
We can see that ones place goes up by 1, the tens place goes up by 1, and the ones place stays the same. But that’s not the pattern that helps us get the answers! Instead of looking down, from one answer to the next, look across from the problem to the answer, to see a pattern.
11 x 11 = 121. What do you notice about the first and last digits of the answer? What do you notice about the middle number?
12 x 11 = 132. What do you notice about the first and last digits of the answer? What do you notice about the middle number?
13 x 11 = 143. What do you notice about the first and last digits of the answer? What do you notice about the middle number? Look at the next multiple of 11 and the answer to see if the pattern holds.
14 × 11 = 154
↑ the same ↑ ↑ and the middle number is 1 + 4
How would you use this pattern to find the answer to 17 × 11?
Question: Now you try! Use the pattern of 11’s to find some new answers. NEED H5P
You may have noticed that we labelled this example as “algebraic reasoning,” even thought there is no variable in it. But we are using the same sort of reasoning we need to use in algebra — starting with a pattern and extending it to a larger set of numbers.
Power point for this class: problem-solving-strategies-for-any-level-of-studentDownload
Homework:

