Sec. 2.4 – Fibonacci Numbers, Figurate Numbers, Non-Linear Equations; Using Subscripts to Find Patterns
Chapter 2, Section 4
Math Topics – Fibonacci Numbers; the Golden Ratio, Figurate Numbers, Successive Differences and Non-Linear Equations; Using Subscripts to Find Patterns
Fibonacci Numbers
The Fibonacci numbers were invented in 1202 by Italian mathematician Leonardo of Pisa, who was also known as Fibonacci. But they also appeared over a thousand years before that in Indian Mathematics in Sanskrit poems. The numbers are rich in beautiful patterns, and appear in nature and in art, in spirals and in rectangles.
The Fibonacci numbers begin: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ….
Each new number is the sum of the previous two. For example, 1+1 =2, 1+2 = 3, 2+3 = 5, 3+5 = 8, etc.
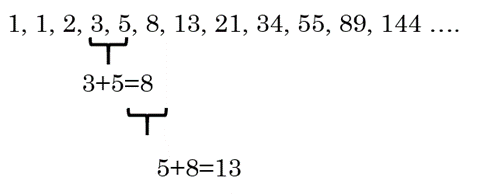
We designate F1 to mean the first Fibonacci number, F2 to mean the second, etc.
F7 = 13 means the 7th Fibonacci number is 13.
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 | F16 | F17 | F18 | F19 |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 |
Question: Now you try! Find F19 and F20.
Flower petals tend to come in Fibonacci numbers.




Sunflower with 21 petals; Shutterstock
The number of spirals in the middle of sunflowers, pinecones, artichokes and pineapples also tend to be Fibonacci numbers.

The Nation Museum of Mathematics (MoMath) has a series of illustrations showing how to count the spirals: https://momath.org/home/fibonacci-numbers-of-sunflower-seed-spirals/ One of their pictures is below:
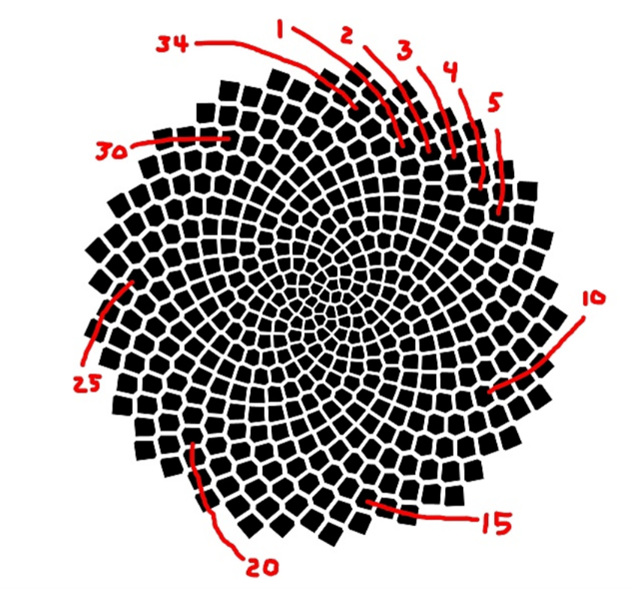

WHY?
This wonderful video by Vi Hart shows how to find Fibonacci numbers in all kinds of plants: https://www.khanacademy.org/math/math-for-fun-and-glory/vi-hart/spirals-fibonacci/v/doodling-in-math-spirals-fibonacci-and-being-a-plant-1-of-3 If you watch the second video in this series, she does a beautiful job of explaining why plants grow in this way – in order to maximize the leaves’ exposure to sunlight, using the most efficient way to grow, because that particular angle is what works just right to give enough space for each leaf.
You can also create a Fibonacci spiral using squares that are the size of Fibonacci numbers.
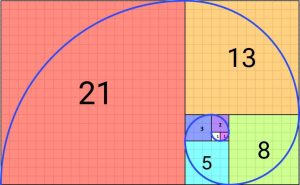
The Fibonacci spiral resembles the spiral of a seashell.

Example 1 Which sequence is most like a Fibonacci sequence?
1, 1, 2, 2, 3, 3 ….
1, 1, 1, 3, 3, 3, 9, 9, 9, 27, 27, 27
2, 5, 7, 12, 19, ….
Try this out yourself, then check here https://koffenholley.survey.fm/fibonacci-quiz to see if you are right!
Try the “quiz” to see which one is right before you scroll down to see why.
<spoiler space>
<spoiler space>
<spoiler space>
Each sequence has some characteristics that are Fibonacci-like. The first sequence, 1, 1, 2, 2, 3, 3 …. starts out with 1, 1, just like the Fibonacci sequence. But then after that, two numbers do not add to equal the next. The next sequence, 1, 1, 1, 3, 3, 3, 9, 9, 9, 27, 27, 27, has an interesting pattern, but you have to add three numbers to get the next and then the number repeats three times — not the same as the Fibonacci pattern. The third sequence, 2, 5, 7, 12, 19, …. is most like a Fibonacci sequence since you must add two numbers to get the next.
Example 2 Divide consecutive Fibonacci numbers. What pattern do you see in the answers? For example, F4/F3 = 3/2 = 1.5 Try dividing the next pair, F5/F4 = 5/3, and the next pair, F6/F5 = 8/5 , etc. What do you notice?
Try it!!! You will remember this better if you stop and think about it than if you hurry to “the answer.” When you teach your own class of students, remember that SPEED often does not equal learning. For grown up students, we are often pressured to go fast so we can cram in more all at once instead of really learning. UGH.
<spoiler space>
<allow time to think and try it!!>
As you divide larger and larger consecutive Fibonacci numbers the result tends to get closer and closer to 1.61… , or more exactly, to ![]() This number is known as the Golden Number, phi, written with the Greek letter, φ . This number is similar to pi = 3.14159…., written with the Greek letter, π. Both have decimals that continue infinitely, and both are irrational numbers (more on irrational numbers in a later section).
This number is known as the Golden Number, phi, written with the Greek letter, φ . This number is similar to pi = 3.14159…., written with the Greek letter, π. Both have decimals that continue infinitely, and both are irrational numbers (more on irrational numbers in a later section).
The Golden Ratio, or “Divine Proportion”
The Ancient Greeks thought that things that were in this ratio were more “pleasing to the eye.” This includes the Parthenon, a temple that was dedicated to the goddess Athena during the fifth century BCE.


Later, Renaissance painters revived the use of the golden ratio. Mona Lisa, by Leonardo DaVinci (painted around 1503) has proportions that are in the golden ratio.
Try it yourself! Measure the length and width of a rectangle that looks pretty to you. Calculate length divided by width. See if it comes out close to the golden number. Do you think the Greeks were right about what kinds of rectangles look the prettiest?
You can also measure from the top of your shoulder to the tips of your fingers and then from the crook of your elbow to the tips of your fingers. The ratio of these two numbers is also often close to 1.618…!
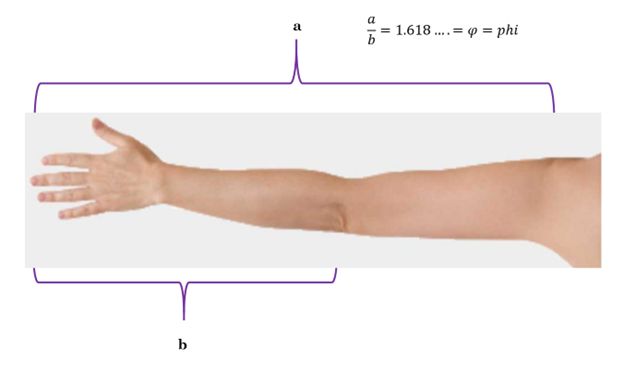
We have tried this in class with students and it works!!
Using Subscripts to Find Patterns
F12
In this part of our problem solving, we will use the subscripts (the small index numbers) to find patterns. The small number, 12, above, is called a subscript. It means the 12th Fibonacci number. When we say that F12 is the sum of the previous two Fibonacci numbers, we can write F12 = F11 + F10, or 144 = 89 + 55, since those are the 12th, 11th and 10th Fibonacci numbers. Notice how 11 is one less than 12, and 10 is 2 less than 12. We could write F12 = F12-1 + F12-2. To find a general formula, use n instead of 12. In general, for all Fibonacci numbers, Fn = Fn-1 + Fn-2.
F12 = F11+F10
F12 = F12-1+F12-2
Fn = Fn-1+Fn-2
To get the general formula using n, we imitate the pattern we see with the numbers themselves.
Example 3 Find the general formula using n for the ratio of two successive Fibonacci numbers, 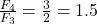 ,
, 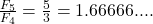 ,
,  , etc., in the pattern we explored before.
, etc., in the pattern we explored before.
To see the formula, notice that the bottom number is always one less than the top. That is,
![]()
and
![]()
To find a general formula, use n instead of 4 in the first example, or use n instead of 5 in the second example. We get
![]()
This is the general formula for the ratio of two successive Fibonacci numbers.
Note: we could have instead started with the bottom number, and noticed that the top number is one bigger, so we could instead write Fn+1/Fn. There is often more than one correct way to write a formula, depending on what we take n to be.
Example 4 An interesting pattern emerges when we add any six consecutive Fibonacci numbers. See if you can find the pattern, then write the general form using subscripts.
Step 1: Understand the problem. Consecutive means one right after the other. So, if we are using just regular integers, the the numbers 3, 4, 5 are one right after another, but 2, 4, 9 are not.
Remember that the Fibonacci numbers are:
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 | F16 | F17 | F18 | F19 |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 |
So now you need to pick six Fibonacci numbers that are one right after another and see what you get when you add them.
Add the first six: F1 + F2 + F3 + F4 + F5 + F6 = 1+1+2+3+5+8 = 20
Add another six that are consecutive: F3+F4+F5+F6+F7+F8=2+3+5+8+13+21 = 52
Add another six consecutive Fibonacci numbers: F5+F6+F7+F8+F9+F10=5+8+13+21+34+55 = 136
Add another six: F6+F7+F8+F9+F10+F11=8+13+21+34+55+89 = 220
What is the largest number that you see that divides into each of these answers? Write each answer as a product using that number.
Each is divisible by 2, but the largest number that goes into each is 4. We can write each answer as a product of the number 4 and another number:
F1 + F2 + F3 + F4 + F5 + F6 = 1+1+2+3+5+8 = 20 = 4 × 5
F3+F4+F5+F6+F7+F8=2+3+5+8+13+21 = 52 = 4 × 13
F5+F6+F7+F8+F9+F10=5+8+13+21+34+55 = 136 = 4 × 34
F6+F7+F8+F9+F10+F11=8+13+21+34+55+89 = 220 = 4 × 55
To see even more of the pattern, write which Fibonacci number you have in each case.
F1 + F2 + F3 + F4 + F5 + F6 = 4 × 5 = 4 × F5
F3+F4+F5+F6+F7+F8 = 4 × 13 = 4 × F7
F5+F6+F7+F8+F9+F10 = 4 × 34 = 4 × F9
F6+F7+F8+F9+F10+F11 = 4 × 55 = 4 × F10
See if you can now see where that Fibonacci number is, in relation to the ones you just added, then write the general pattern in words and using n. Notice that, just like with the pattern of 9’s and the pattern of 11’s, we are going across from the problem to the answer to try to find the pattern.
In words: You get four times the fifth Fibonacci number of the ones you added.
Using subscripts: Fn + Fn+1 + Fn+2 + Fn+3 + Fn+4 + Fn+5 = 4 × Fn+4
Figurate Numbers
The figurate numbers make common figures, or shapes. There are triangular numbers (that make triangles or pyramids), square numbers (that make squares), pentagonal numbers (that make 5-sided shapes called pentagons), and more.
Square Numbers
You have already seen the square numbers, so we’ll start with those. The square numbers are the perfect squares: 1, 4, 9, 16, 25, etc. We write S1 to indicate the first square number, S2 for the second square number, and so on.
When we draw the square numbers, we can represent them as square shapes:
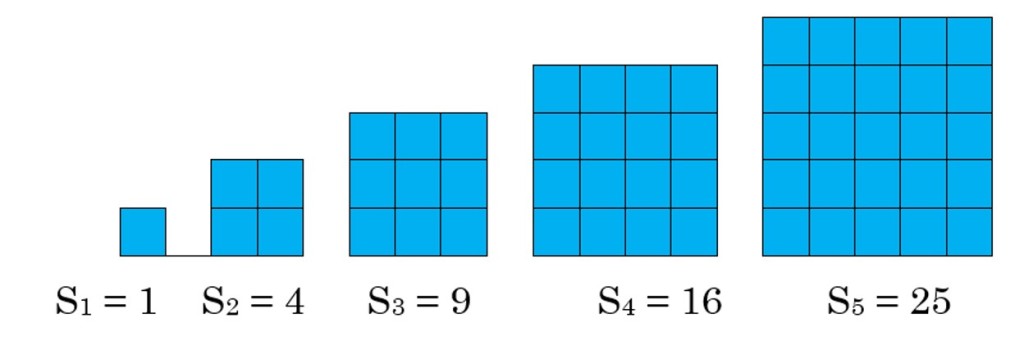
Example 5 Use the formula Sn = n2 to find the 6th square number, and draw the picture.
We replace the n in the formula with the number 6, so S6 = 62 = 36. The picture will be a 6 by 6 square.
Example 6 Find the successive differences for the square numbers. Use the differences to predict the next square number.
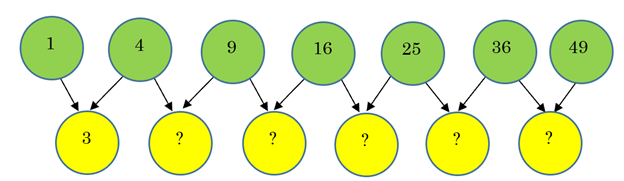
That is, 4 – 1 = 3, so place 3 between the two numbers. Next, find 9 – 4, then 16 – 9, etc. What do you notice about each new difference?

You may notice that the differences don’t stay the same each time – in fact, they are changing by 2 each time! If you make one more row of differences, you can see this even more clearly.
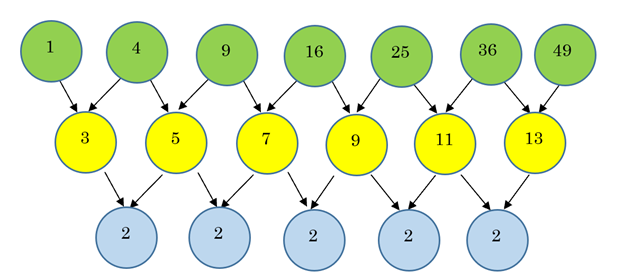
Next, we can use these differences to work backward to finding out the next number in the sequence:
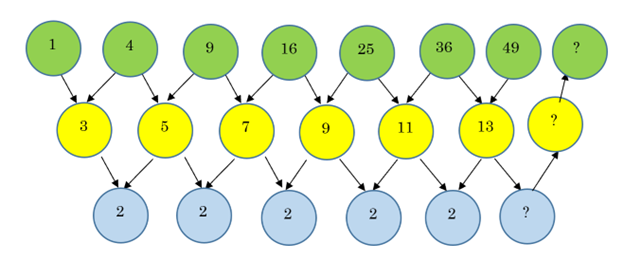
Start at the blue circle on the bottom right. What number does that have to be? Next, what does that tell you the next yellow circle must be? Finally, what does that mean we have to add to get the next square number?
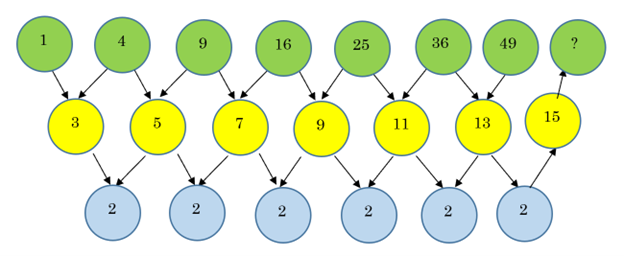
We know the next blue circle must also be a 2, so the yellow circle above it must be 13 + 2 = 15. Thus, the next square number must be 49 + 15 = 64.
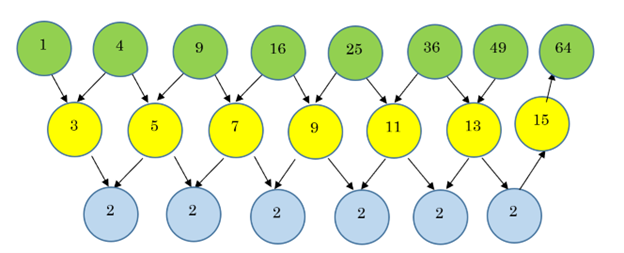
We can also verify this because we know that 82 = 64.
Notice that it took two rows of differences before we got the same difference every time. Recall that the differences are the slope of the equation, so this means our slope is constantly changing! This means that if we make a table of the square numbers and graph them, we will not get a straight line.
We can write our table horizontally, as below.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| n2 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 |
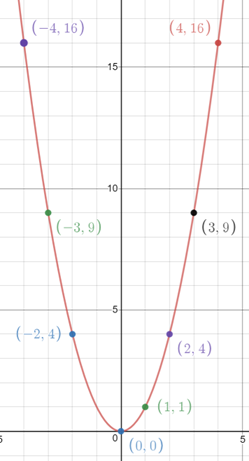
Or, writing the table vertically, as we usually do when graphing, we have:
| x (or n) | y | point |
| -4 | 16 | (-4,16) |
| -3 | 9 | (-3,9) |
| -2 | 4 | (-2,4) |
| -1 | 1 | (-1,1) |
| 0 | 0 | (0,0) |
| 1 | 1 | (1,1) |
| 2 | 4 | (2,4) |
| 3 | 9 | (3,9) |
| 4 | 16 | (4,16) |
Notice that for the table, we extended the pattern to include negative numbers.
We can graph these points and see that we have a parabola. Notice that the left and right sides of the parabola have the same y-values, since when we square a negative number, we get a positive value.
Algebra note: Linear and Non-Linear Equations
A linear equation (which graphs a line) with x1 as the highest-powered term, will have one row of successive differences which will remain the same each time – that difference is the slope of the line, so we can use y=mx+b to find the equation.
A quadratic equation (which graphs a parabola) with x2 as the highest-powered term, will have two rows of successive differences before we get a difference that stays the same each time. To find the equation, we might need to use calculus, using the derivative, or if it’s a block pattern, we may be able to visualize the physical squares in the pattern, and how those squares relate to the x values.
An equation with x3 as the highest-powered term, will have three rows of successive differences before the difference stays the same each time.
Triangular Numbers
Another type of figurate number (numbers that make a shape) is the triangular number.
For the triangular numbers, we write T1 to mean the first triangular number, T2 to mean the second triangular number, and so on. If we use blocks, the triangular numbers are shaped like pyramids.
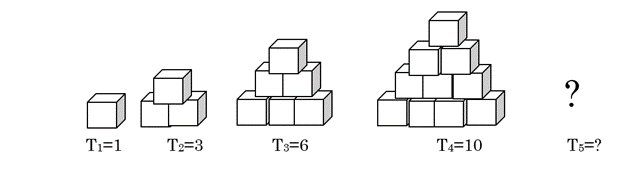
The first triangular number has 1 block, so T1 = 1; the second triangular number has 3 blocks, so T2 = 3; T3 = 6 and T4 = 10.
If we use dots, the shapes look more like triangles, and coloring the bottom row can help us see how the number in that bottom row relates to the triangular number we are on.
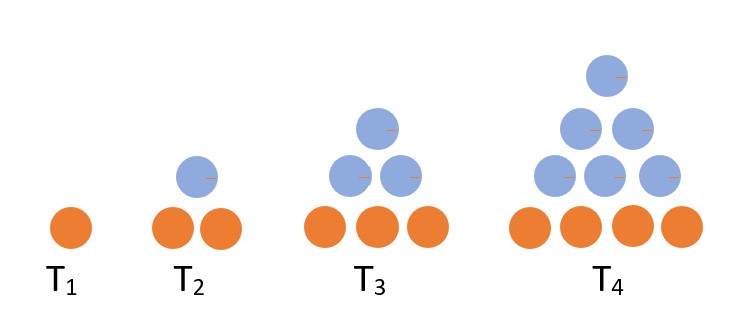
Example 7 See if you can draw the correct picture for T5 by copying the picture for T4 (either using dots or blocks, your choice) and adding one more layer of blocks or dots to the bottom row. How many blocks will be in the bottom row of T5? How many total blocks does T5 have?
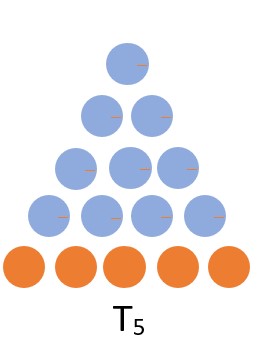
The bottom row in T5 will have 5 blocks in it, the same as the subscript (the small 5). The total number of blocks will be 1+2+3+4+5 = 15. Thus, T5 = 15. How many blocks will be in the bottom row of T6? How many total blocks will it have?
Spoiler space….
See if you can figure it out before you scroll down!
….
….
….
The bottom row of T6 will have 6 blocks, the same as the subscript 6. The total number of blocks will be 1+2+3+4+5+6 = 21. Thus, T6 = 21.
Another way to find the triangular numbers is to use the formula for triangular numbers, which is:
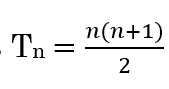
You can use this formula to see that T5 should have 15 blocks, by letting n = 5 in the formula:
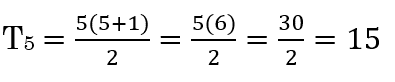
Example 8 Use the triangular number formula to find the 6th and 7th triangular numbers.
For the 6th triangular number, let n = 6 in the formula. We get T6 = 6(6+1)/2 = 6(7)/2 = 42/2 = 21
For the 7th triangular number, let n = 7 in the formula. Try it yourself. The answer should be 28.
Example 9 Find the successive differences for the triangular numbers and use them to find the 5th, 6th and 7th triangular numbers. Your answers should agree with what you got in the formula, above.
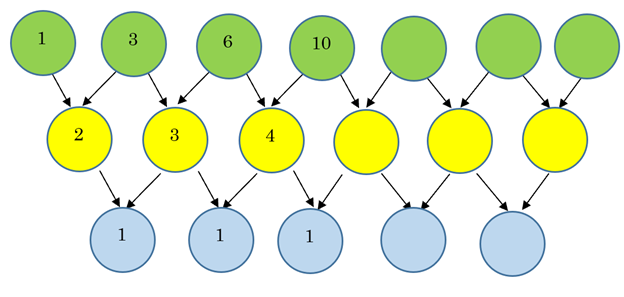
Example 9, continued
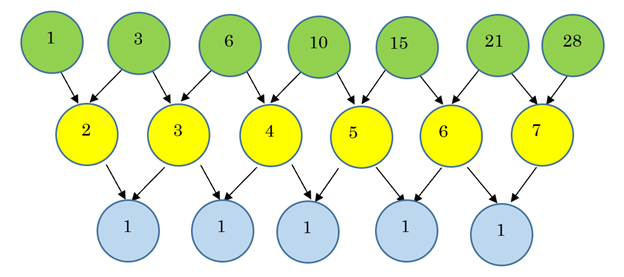
Notice that it again takes two rows for the differences to remain constant. This is consistent with the fact that the triangular number formula,
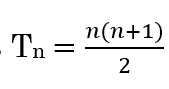
can be rewritten as
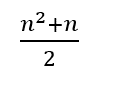
so the highest power is the 2nd power, as expected by the fact that it took two rows for the difference to remain constant.
