Sec. 2.5 – Fractions, Patterns in Pascal’s Triangle
Chapter 2, Section 5
Elementary Education – Introduction to Fractions, Equivalent Fractions, Fraction Size, Adding Fractions
Math Topics – More Problem Solving: Pascal’s Triangle
Introduction to Fractions
Before children formally learn fractions, they can play with Tangrams and attribute blocks to make shapes and begin to explore how shapes can fit into a whole.

Even pre-school aged children understand the fraction 1/2, and most understand how to share equal amounts of objects. In Developing Effective Fractions Instruction for Kindergarten through 8th Grade, the authors recommend building on this sort of informal understanding by having kindergarten children start with sharing problems that involve whole numbers, like sharing 12 cookies with 3 people.

As children get older, such problems can progress to those with fraction results, like sharing 4 pizzas among 8 children.
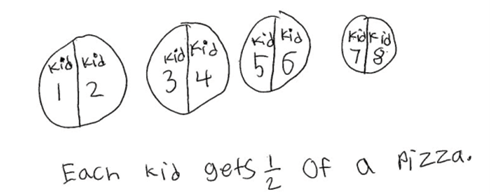
What is a Fraction?
In about the third grade, children begin formal instruction in fractions. Fractions can be understood as a part of a whole and at the same time as a particular place on the number line, as a number. For example, ![]() can be thought of as 1 part of a whole that is divided into 2 pieces; it can also be thought of as the number that is half way between 0 and 1 on the number line.
can be thought of as 1 part of a whole that is divided into 2 pieces; it can also be thought of as the number that is half way between 0 and 1 on the number line.

Similarly, ![]() can be thought of as 1 part of a whole that is divided into 4 pieces, or one quarter of the way between 0 and 1 on the number line.
can be thought of as 1 part of a whole that is divided into 4 pieces, or one quarter of the way between 0 and 1 on the number line.

For ![]() , we can think of taking three out of 4 equal parts, or of dividing the number line into 4 equal parts and going to the third part.
, we can think of taking three out of 4 equal parts, or of dividing the number line into 4 equal parts and going to the third part.

It is also important for children to use many other objects to represent fractions, not just pizzas and the number line! By using many kinds of objects, students can visualize parts of many different kinds of wholes, and can begin to see equivalent fractions.
Example 1 Using the milk carton pack that has 24 cartons of milk, below, show the fractions 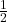 ,
, 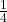 , and
, and 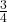 .
.

To show ![]() , we take the milk pack and cut it into two equal parts, circling or shading one of those parts. You can cut this particular carton in half horizontally or vertically.
, we take the milk pack and cut it into two equal parts, circling or shading one of those parts. You can cut this particular carton in half horizontally or vertically.

To show ![]() , we take the milk pack and cut it into four equal parts, circling or shading one of those parts.
, we take the milk pack and cut it into four equal parts, circling or shading one of those parts.

To show ![]() , we take the milk pack and cut it into four equal parts, circling or shading three of those parts.
, we take the milk pack and cut it into four equal parts, circling or shading three of those parts.

The key take-away: ![]() is splitting an object into 4 equal parts and taking 3 of them.
is splitting an object into 4 equal parts and taking 3 of them.
![]() is splitting an object into b equal parts and taking a of them. The number in the denominator (bottom) or the fraction, is the number of equal parts, while the top number (the numerator) is the number you take, or circle.
is splitting an object into b equal parts and taking a of them. The number in the denominator (bottom) or the fraction, is the number of equal parts, while the top number (the numerator) is the number you take, or circle.
Example 2 Using the pack of 15 soup cans, below, show the fractions 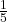 and
and 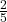 .
.

To show ![]() , divide the pack into five equal parts and take one of them. To show
, divide the pack into five equal parts and take one of them. To show ![]() , divide the pack into five equal parts and take two of them.
, divide the pack into five equal parts and take two of them.

Question: Now you try! How would you take the same cans of soup and show ![]() ? How would you make the numerator of 1 and the denominator of 3 a clear part of your picture? How would you show
? How would you make the numerator of 1 and the denominator of 3 a clear part of your picture? How would you show ![]() ? How would you make the numerator of 2 and the denominator of 3 a clear part of your picture? Click here after you think about it.
? How would you make the numerator of 2 and the denominator of 3 a clear part of your picture? Click here after you think about it.
Equivalent Fractions
Using real objects to create fractions can begin to allow students to see equivalent fractions, which are fractions that have the same value, even though they look different. For example, in the above soup can example, the fraction ![]() is equivalent to 3 cans out of 15. That is,
is equivalent to 3 cans out of 15. That is, ![]()
Numerically, to get an equivalent fraction, we multiply or divide the top and bottom of the fraction by the same number. For example, we can multiply the numerator (top) of ![]() by 3 and the denominator (bottom) of
by 3 and the denominator (bottom) of ![]() by 3 to get
by 3 to get ![]() .
.
![]()
Or we can divide ![]() by
by ![]() to go back to
to go back to ![]() :
:
![]()
Either way creates an equivalent fraction because multiplying or dividing by 3/3 is the same as multiplying or dividing by 1.
Example 3 Using the pack of soup cans, find the fraction equivalent to 2/5.
Since we circled six cans out of a total of 15 cans, we know that 2/5 is equivalent to 6/15.
We can also show this numerically, by multiplying ![]() by
by ![]() . That is,
. That is, ![]()
We can also divide ![]() by
by ![]() to go back to
to go back to ![]() :
:
![]()
Question: Now you try! If you have 15 cans of soup, what fraction equivalent to 1/3 would that give you? How could you get that fraction looking at the picture? How could you get that fraction numerically, by multiplying? What about 2/3? Click here after you think about it.
But for children first learning fractions, being able to picture the fractions should come first, before you do the arithmetic, so that the arithmetic makes sense.
Example 4 Using tangrams or pattern/attribute blocks, if the hexagon is one whole, how can you show halves, thirds and sixths? What about 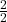 ,
, 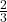 , and
, and 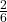 ? What equivalent fractions can we see?
? What equivalent fractions can we see?
If a hexagon is one whole, then the trapezoid is ½, since 2 trapezoids fit into a hexagon.

1 whole hexagon, ![]() hexagon = trapezoid,
hexagon = trapezoid, ![]() two trapezoids = 1 whole hexagon.
two trapezoids = 1 whole hexagon.
Since three rhombuses (diamonds) fit in a hexagon, one rhombus = ![]()

One-third = one part shaded out of three equal parts
We can show ![]() by shading 2 of them.
by shading 2 of them.

Two-thirds = two parts shaded out of three equal parts
If we shade all three parts, we have ![]() = 1 whole
= 1 whole

Three thirds = 1 whole
The hexagon can be divided into 6 triangles, so 1 triangle = ![]()

Notice that ![]() makes the same shape as
makes the same shape as ![]() .
.
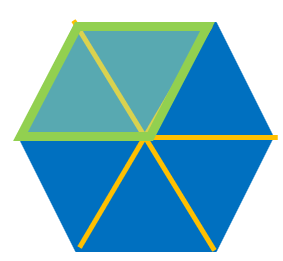
Since two triangles = one rhombus, we can see naturally that ![]()
Numerically, we can divide ![]() by
by ![]() to get
to get
![]()
The two fractions ![]() and
and ![]() are equivalent because dividing by
are equivalent because dividing by ![]() is the same as dividing by 1.
is the same as dividing by 1.
Notice that the hexagon divides nicely into halves, thirds and sixths, but it would be hard to show ![]() or
or ![]() using a hexagon, since it is hard to divide a hexagon into 4 equal parts or 5 equal parts.
using a hexagon, since it is hard to divide a hexagon into 4 equal parts or 5 equal parts.
Relative Sizes of Fractions
It can be confusing that the fraction ![]() is bigger than the fraction
is bigger than the fraction ![]() , even though 2 is smaller than 6. But when children use Tangrams or attribute blocks, they can see that one half of a hexagon (the trapezoid) is much bigger than one-third (the triangle). Relative fraction sizes can also be experienced using other objects, like boxes of crayons.
, even though 2 is smaller than 6. But when children use Tangrams or attribute blocks, they can see that one half of a hexagon (the trapezoid) is much bigger than one-third (the triangle). Relative fraction sizes can also be experienced using other objects, like boxes of crayons.
Example 5 Using a box of 24 crayons, show which fraction is bigger, 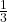 , or
, or 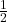 .
.
One third of a box of crayons means we break the box up into three equal parts.

 One-half of a box of 24 crayons is 12 crayons.
One-half of a box of 24 crayons is 12 crayons.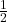 is more than
is more than 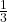
But why not just use fraction bars or pies to show fractions?
Students of all ages tend to do strange things with fraction bars, like making one bar longer than the other:
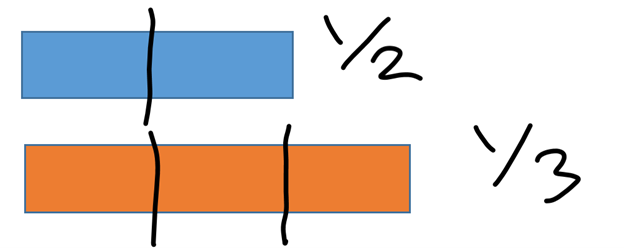
This can lead to the absurd conclusion that ![]() and
and ![]() are the same size, something we would never think when using real objects. Although using pies (circles) doesn’t have this issue, it also doesn’t give students the experience of the meaning of fractions in the same way that using actual objects does.
are the same size, something we would never think when using real objects. Although using pies (circles) doesn’t have this issue, it also doesn’t give students the experience of the meaning of fractions in the same way that using actual objects does.
Measuring Tape Fractions
Most of the world uses the metric system to measure. The metric system is based on tenths.

However, in the United States, we still measure using inches, which are divided into halves, quarters, sixteenths and 32nds.
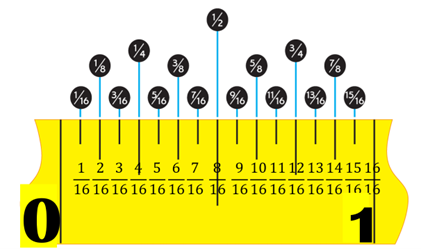
On the measuring tape above, the smallest marks show sixteenths, since there are 16 of them from 0 to 1. When you count the marks, start counting at the first mark after 0.
The next larger marks represent eighths, since you can count that there are 8 marks, separating the line into 8 parts. The next marks are quarters. The largest mark, in the middle, is for ![]() .
.
You can see that ![]() . Several other equivalent fractions can also be seen, such as
. Several other equivalent fractions can also be seen, such as ![]() , and
, and ![]() . The beginning starts at zero, which is the same as
. The beginning starts at zero, which is the same as ![]() .
.
Notice that it is hard to show thirds, fifths or tenths on this ruler, since 16 is not divisible by 3, 5 or by 10.
Example 6 What mixed number is shown by the x on the inch ruler below? What equivalent fraction is also shown?

There are 16 small marks between the 2 and the 3 (don’t count the 2, since that’s the starting spot, but do count the last mark at 3). Thus, the smallest marks are 16ths.
Thus, the x marks two and 14/16:
![]()
Alternatively, you can count out 7 of the 1/8-inch marks.
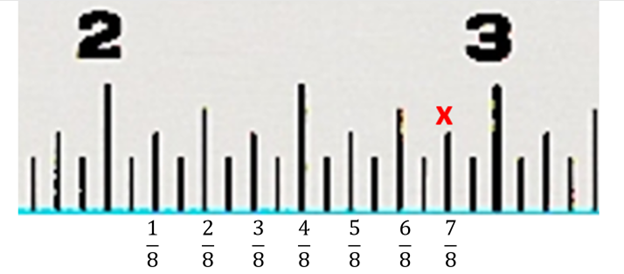
The equivalent fraction is two and 7/8:
![]()
Example 7 Show the fractions 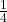 ,
, 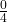 ,
, 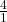 and
and 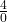 using a measuring tape.
using a measuring tape.
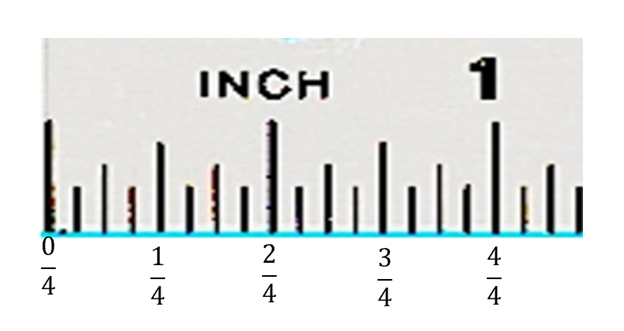
On the measuring tape, the first mark, at 0, shows ![]() .
.
The fraction ![]() is the same as 4 whole objects. It is not shown on the above measuring tape, because it is all the way over at 4 inches. See the picture below.
is the same as 4 whole objects. It is not shown on the above measuring tape, because it is all the way over at 4 inches. See the picture below.

To show the fraction ![]() , we would have to break an object into zero pieces, and then shade 4 of them. This is impossible! Similarly, we cannot show
, we would have to break an object into zero pieces, and then shade 4 of them. This is impossible! Similarly, we cannot show ![]() on a measuring tape. The fraction
on a measuring tape. The fraction ![]() is undefined.
is undefined.
In general, any number divided by zero is undefined.
Why?
We know that a division problem like 12 ÷ 3 = 4 has a matching multiplication problem 3 × 4 = 12.
That is, ![]() gives us 3 × 4 = 12
gives us 3 × 4 = 12
Similarly, ![]() has the matching multiplication problem 3 × 0 = 0.
has the matching multiplication problem 3 × 0 = 0.
Generally, we know that ![]() , because b × 0 = 0.
, because b × 0 = 0.
However, ![]() , with zero in the denominator (bottom of the fraction) is a different matter. Any number we try for an answer would not give us a true multiplication fact, because
, with zero in the denominator (bottom of the fraction) is a different matter. Any number we try for an answer would not give us a true multiplication fact, because ![]() gives us the multiplication 0 × c = a, which cannot be true, unless a is zero. The answer is not true for any other value of a. For example, suppose we have
gives us the multiplication 0 × c = a, which cannot be true, unless a is zero. The answer is not true for any other value of a. For example, suppose we have ![]() . This gives us 0x = 3, which then gives us 0 = 3, which is never true.
. This gives us 0x = 3, which then gives us 0 = 3, which is never true.
To go back to our concrete examples, if a hexagon is the whole, we cannot show ![]() because that would mean dividing the hexagon into zero parts, and taking (or circling) three of them. That is not possible!
because that would mean dividing the hexagon into zero parts, and taking (or circling) three of them. That is not possible!

A hexagon divided into zero parts. How can we take three of the parts?
That’s impossible!
Question: Now you try!

CHANGE INTO H5P On the above measuring tape, how could you show the fractions 0/3, 3/0, and 3/1? Roughly where would 1/3 be, and why would it be hard to show using the existing marks on the tape? Click here after you think about it.
Adding and Subtracting Fractions Using Models and “Like Terms”
Children can use attribute blocks and other objects to model adding fractions. For example, the hexagons below shows that ![]()
 = 1 whole
= 1 whole
Adding these two fractions is similar to adding like terms in algebra, in that the like term stays the same:
two thirds + one third = three thirds (not three sixths)
![]() (not
(not ![]() )
)
![]() (not
(not ![]() )
)
two triangles + one triangles = three triangles (not three of a new shape)
Adding and Subtracting Fractions That Do Not Have the Same Denominator
To model fractions that do not have the same denominators, we can continue to use the hexagons, egg cartons, bags, etc., to show how to re-divide the objects into smaller pieces that are the same size, so they can be added.
Example 8 Use a hexagon to model 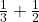 .
.
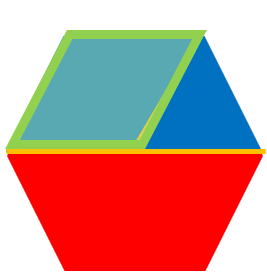
In this picture, we have one green rhombus, which represents ![]() .
.
We have one red hexagon, which represents ![]() .
.
A child who has previously used the hexagon, rhombus, triangle and trapezoid tangram shapes may recognize that since we have 1 blue triangle remaining out of 6 that make a hexagon, the answer to ![]() must be 5 blue triangles, or
must be 5 blue triangles, or ![]() .
.
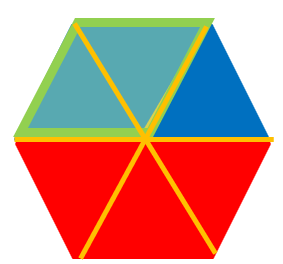
Alternatively, the child may see that ![]() is the same as three blue triangles and
is the same as three blue triangles and ![]() is the same as two blue triangles, so
is the same as two blue triangles, so
one half + one third = three triangles + two triangles = five triangles = ![]()
We can also multiply ![]() by 3/3 to get 6ths, and multiply
by 3/3 to get 6ths, and multiply ![]() by 2/2 to get 6ths:
by 2/2 to get 6ths:
![]()
Example 9 Show how you could add 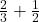 using egg cartons. Think of how you can use the fact that there are 12 eggs in a carton to give you a common denominator, and how you can explain why the answer comes out to more than one whole.
using egg cartons. Think of how you can use the fact that there are 12 eggs in a carton to give you a common denominator, and how you can explain why the answer comes out to more than one whole.
To show ![]() , we can use an egg carton divided into three equal parts with two parts circled or shaded.
, we can use an egg carton divided into three equal parts with two parts circled or shaded.

Since there are 12 eggs, and we circled 8 of them, we get the equivalent fraction ![]() .
.
We know numerically that ![]() because when we divide the numerator and denominator by 4, we get the fraction
because when we divide the numerator and denominator by 4, we get the fraction ![]() :
: ![]() .
.
We can also think of multiplying ![]() by 4/4 to get
by 4/4 to get ![]() :
:
![]()

To show ![]() , we can use an egg carton divided into two equal parts with one part circled or shaded. This is the same as 6 eggs out of 12, or
, we can use an egg carton divided into two equal parts with one part circled or shaded. This is the same as 6 eggs out of 12, or ![]() .
.
Make sure you can see how to get this fraction numerically as well. What would you multiply ![]() by to get
by to get ![]() ?
?
Putting all the eggs together gives us ![]()

![]()
Since 14 eggs is more than 1 carton, we have 1 carton + 2 eggs in the next carton = ![]()
A child may notice that the two eggs are 1/6 of the remaining carton, so that we can write ![]() instead of
instead of ![]() , but for early exploration, it is not important to always simplify the fractions.
, but for early exploration, it is not important to always simplify the fractions.
Notice that in this example, we did not use the lowest common denominator, which would have been 6. Instead, we used the denominator that was suggested by the objects we used.
Question: Now you try!
Using 15 cans of soup, how could you show how to add 2/3 + 3/5? What common denominator would be suggested by the cans? How would you know whether the answer would come out to more than 1 whole? Click here after you think about it.
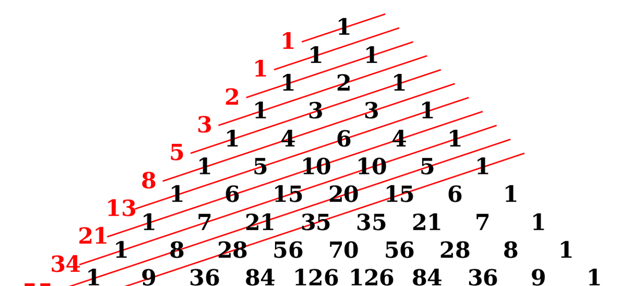
More Problem Solving: Pascal’s Triangle Guess My Rule
The first two rows of Pascal’s Triangle are shown below. Can you tell what the next row will be?
1 1 1
Of course not! Remember, two examples of a pattern (in this case, two rows) is rarely enough to determine a pattern.
Can you tell what the next row will be now, using the three rows shown below?
1
1 1
1 2 1
Maybe! Hint: think of how the 1 and the 1 combine to make the 2 below them.
You might find that you really need one more example before you can see a pattern….
1
1 1
1 2 1
1 3 3 1
See if you can figure out the next row now!
The pattern is that you add the numbers above, to the left and right, to get the next number. For example, we get the 6 by adding the 3 and the 3 above it.
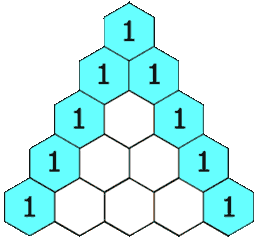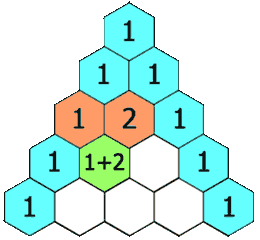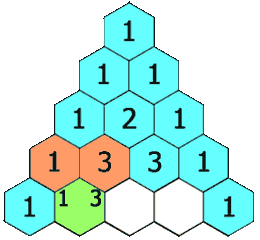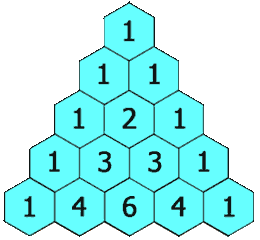
There are many interesting patterns in Pascal’s triangle. The next examples show a few of them.
Example 9 Can you find the Natural Numbers (1, 2, 3, 4, ….) in order in Pascal’s Triangle?
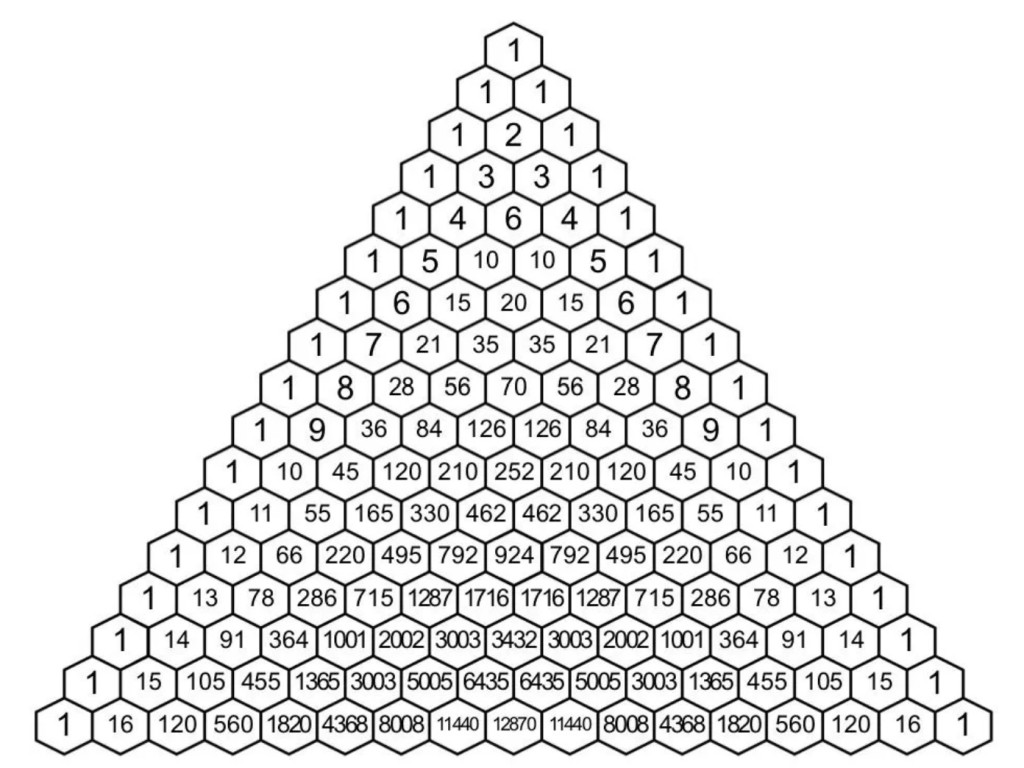
The Natural Numbers (1, 2, 3, ….) appear in order along the first and last diagonal.
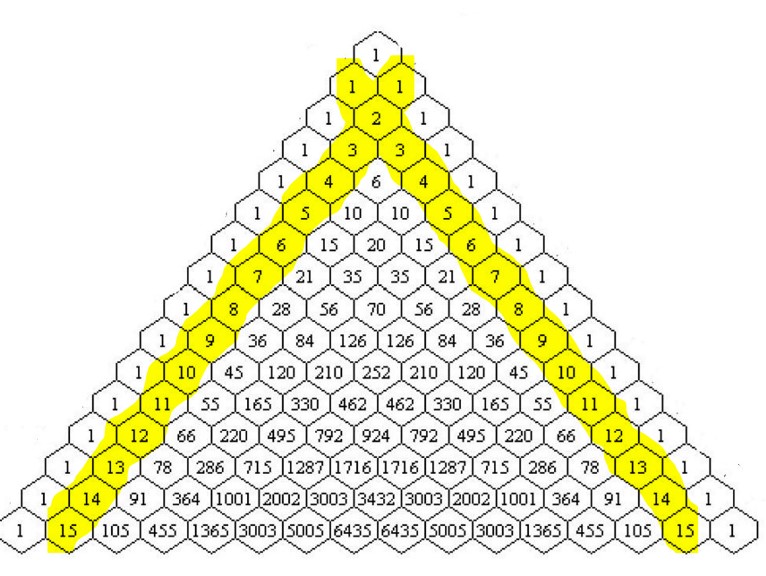
Example 10 Another pattern occurs if we add up each row.
The top row, which we’ll call row zero, just has 1, so it adds up to 1.
The next row, row 1, has 1 and 1 in it, which add up to 1+1 = 2.
The third row, 1, 2, 1, adds up to 1+2+1 = 4.
The fourth row, 1, 3, 3, 1, adds up to 1+3+3+1 = 8.
Do you see a pattern in the answers? How can you use the pattern to predict the number in the next row?
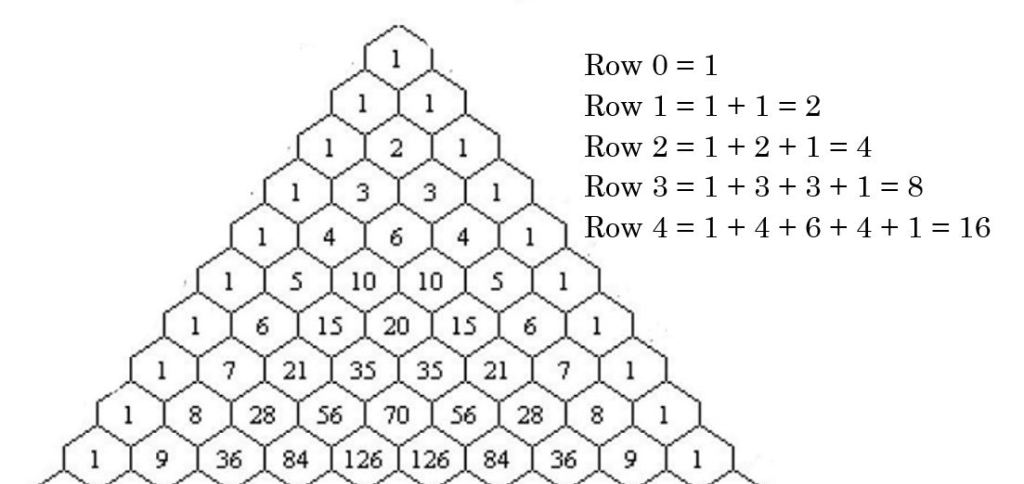
The answers double each time, so we know the next row will add up to 16 (shown above), and the one after that will add up to 32.
What do you think the 30th row will add up to? To find out using the pattern of the answers, we would have to keep doubling and doubling! But there is an easier way, using algebraic reasoning. Instead of looking down, from one answer to the next, let’s look across, and see how each row number relates to each answer.
Row 0 = 1
Row 1 = 2
Row 2 = 4
Row 3 = 8
Row 4 = 16
How can you use the row number to get the answer?
Hint: when we double, we are multiplying by 2, over and over. Repeated multiplication is represented by exponents. So, repeatedly multiplying by 2 is the same as raising 2 to a power. Now see if you see a pattern!
Row 0 = 1 = 2?
Row 1 = 2 = 2?
Row 2 = 4 = 2?
Row 3 = 8 = 2?
Row 4 = 16 = 2?
What power of 2 do you get for each answer? How is that related to the row number?
Row 0 = 1 = 20
Row 1 = 2 = 21
Row 2 = 4 = 22
Row 3 = 8 = 23
Row 4 = 16 = 24
Using the powers of 2, it is much easier to find the sum of the 30th row, without actually having to add up the 30th row.
The 30th row will have the sum, 230
= 1,073,741,824 Wow!
In general, since the row number and the exponent are the same, we can write that row n will have the sum 2n . We use the same letter to represent the row number and the exponent.
Example 11 Another pattern in Pascal’s triangle
If we make more shallow diagonals, like this, and add up the numbers along them, what types of numbers do you see?
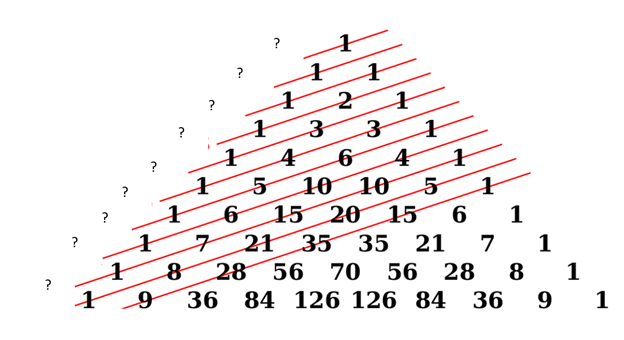
We get the Fibonacci numbers if we add along the diagonals shown!