Sec. 2.6 – Babylonian Fractions; Writing Terminating and Repeating Decimals as Fractions; Multiplying Fractions Visually
Chapter 2, Section 6
Math Topics – Babylonian Fractions; Writing Terminating and Repeating Decimals as Fractions
Elementary Education – Introduction to Multiplying Fractions Visually; Kitchen Math
Babylonian Fractions

This stone tablet, from approximately 4,000 years ago, shows Babylonian fractions written on the diagonal of a square. The number 1, followed by 21, then 51, then 10, shows a 1 followed by three Babylonian fractional place values.
The Babylonians used 60 as the base for their fractions, as well as their whole numbers!
Thus, to figure out a Babylonian fraction, you must try to find an equivalent fraction over 60.
For example, to figure out the Babylonian fraction for ½, ask yourself, 1/2 = what/60?
![]()
To get 60 in the denominator, we must multiply the 2 by 30. Since we must multiply numerator (top) and denominator (bottom) of the fraction by the same number, we must also multiply the 1 by 30:
![]()
Thus, the Babylonian equivalent to our ½ is 30. The Babylonians used three of the symbols for ten to make 30: 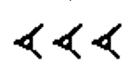 to show this fraction, just as they would show the number 30.
to show this fraction, just as they would show the number 30.
Before looking at the chart, below, see if you can figure out the Babylonian fractions for 1/3, 1/4, 1/5 and 1/6.
| Fraction in Our System | Babylonian Fraction | Explanation |
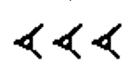
30 |
||
20 |
||
15 |
||
12 |
||
10 |
Example 1 Write 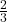 as a Babylonian fraction, using Babylonian symbols.
as a Babylonian fraction, using Babylonian symbols.
Use the strategy of multiplying the numerator and denominator (top and bottom) of the fraction by the same number to get an equivalent fraction.
![]()
Tip: think about what you need to multiply 3 by, to get 60, then do the same thing with the top of the fraction.
We know 3 × 20 = 60, so multiply top and bottom by 20:
![]() =
= ![]()
![]()
![]()
![]()
Note that they did not write the 40 over 60, they just wrote 40 to mean 2/3. People who were reading the number would have to know by context that the number written was a fraction, and not a decimal.
How could you find the Babylonian fractions for
It was easy to write Babylonian fractions for halves, thirds, fifths, sixths, 12ths, 15ths, 30ths, and more – anything that divides evenly into 60.
To make fractions besides these, the Babylonians went to the next place values.
For example, 1/8 could not be written over 60, since 8 does not divide into 60, so it was written as ![]()
You can see that it is true that ![]() by writing each as decimals:
by writing each as decimals:
![]() (divide 1 ÷ 8 on your calculator to see this.)
(divide 1 ÷ 8 on your calculator to see this.)
Or you can get a common denominator and then add:
![]()
450/3600 simplifies to 1/8.
Note: Writing 1/8 as 7/60 + 30/3600 is similar to the way we write the decimal 0.25 as 25/100 = 2/10 + 5/100. We are thinking of the two place values for 0.25, the tenths and hundredths. The Babylonians were thinking of the two places for 1/8, the 60’s place and the 3600’s place.
Example 2 How would the Babylonians have added 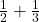 ?
?
The Babylonian fraction for ![]() is
is ![]() , written
, written 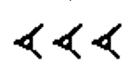 . The Babylonian fraction for
. The Babylonian fraction for ![]() is
is ![]() , written
, written ![]() .
.
To add the two, the Babylonians only had to add 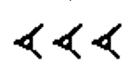 +
+![]() =
= 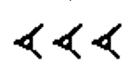
![]() .
.
Note that they did not write the denominator, 60.
In Babylonian, the fractions ![]() and
and ![]() were already “like terms” – they had the common denominator of 60. So they would have added
were already “like terms” – they had the common denominator of 60. So they would have added ![]() .
.
Example 3 How would the Babylonians have added 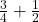 ? How would they have known that the result was more than 1 whole?
? How would they have known that the result was more than 1 whole?
The first fraction has a denominator if 4. We want it to have a denominator of 60, since that’s what the Babylonians used. To go from a denominator of 4 to a denominator of 60, think about what you can multiply 4 by, to get 60.
There are many strategies! You can use guess and check, to see what times 4 gets 60, or you can work backwards, by dividing 60 by 4. Either way, you should get that 4 x 15 = 60, so you need to multiply both numerator and denominator by 15.
![]() =
= 
When the two are added, the result is 75. Since 1 whole = ![]() , the result of
, the result of ![]() is more than one whole.
is more than one whole.
Question: Now you try!
How would the Babylonians have added ![]() and
and ![]() ? Would the result have been more than one whole? How could they tell? Click here to check your answers.
? Would the result have been more than one whole? How could they tell? Click here to check your answers.
Writing Fractions as Decimals and Decimals as Fractions
Any fraction can be written as a decimal, by dividing: numerator (top) ÷ denominator (bottom).
For example, ![]()
![]()
Notice that the first decimal ends, while the second one repeats infinitely.
How can we go the other way, and convert a decimal to a fraction? Notice that 0.4 is called “four tenths.” So we can write it as ![]() , which we can then reduce to
, which we can then reduce to ![]() . Additional examples:
. Additional examples:
![]() , written over ten, since it ends in the tenths place.
, written over ten, since it ends in the tenths place.
![]() , written over 100, since it ends in the hundredths place. We can then reduce this to
, written over 100, since it ends in the hundredths place. We can then reduce this to ![]()
Any decimal that ends can be written as a fraction using the correct power of 10. The power of ten that you need matches the number of decimal places. For example, any decimal that ends after one decimal place would be over 10, or 10 to the 1st power; any decimal that ends after two decimal places would be over 100, or 10 to the 2nd power; any decimal that ends after three decimal places would be over 1000, or 10 to the 3rd power.
Question: Now you try!
How would you write 0.7 as a fraction? What about 0.21? 0.213? Click here to check your answers.
It is a bit more difficult to write a decimal as a fraction if it does not end. For example, the decimal 0.66666… does not end, so it is not possible to decide whether to write it over 10, 100, 1000, or other power of 10.
To write a repeating decimal as a fraction, we can use the problem strategy of writing the problem algebraically:
Start with x = 0.66666….
If we multiply by 10, we move the decimal over one place: 10x = 6.6666….
Why would we do this? Because now if we subtract the two algebraic equations, we can get rid of the repeating decimal, since 6 – 6 = 0:
10x = 6.6666….
–x = 0.6666….
9x = 6 Divide both sides of the equation by 9, and we get ![]()
You can check to make sure you have the right answer by dividing: ![]()
Yes, it worked!
Example 4 Write the following decimals: 0.04, 0.042 and 0.042042042…. as fractions. Be sure to reduce, if possible, and check that you are correct be dividing.
0.04 ends in the 100ths place (two places after the decimal), so we write ![]() , which reduces to
, which reduces to ![]()
Checking by dividing: 1 ÷ 25 = 0.04.
0.042 ends in the1000ths place (three places after the decimal), so we write it as ![]() , which reduces to
, which reduces to ![]()
Checking by dividing: 21 ÷ 500 = 0.042.
The decimal 0.042042… does not end, so we cannot write it over a power of 10.
Instead, we use algebra, starting with x = 0.042042042…. Since the repeat is three digits long, multiply by 1000 to move the decimal over three places: 1000x = 42.042042042….
Now if we subtract the two algebraic equations, we can get rid of the decimal:
1000x = 42.042042….
–x = 0.042042….
999x = 42 Divide both sides of the equation by 999, and we get ![]()
Check by dividing: 14 ÷ 333 = 0.042042… It worked!
Question: Now you try!
Check your understanding of how to convert repeating decimals into fractions! If you have the repeating decimal 0.777777…. what would you let x equal, and what would you multiply x by? What about 0.7070707070….? What about 0.770770770770770….? Click here to check your answers.
Introduction to Multiplying Fractions
Multiplication of fractions can be shown in several ways, some of which may be new to you: taking part of a part, as repeated addition, as area, or using partial products.
Taking a part of a part
What is half of one half? If we look at a measuring tape, ½ is right in the middle.
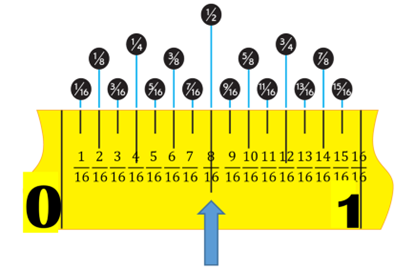
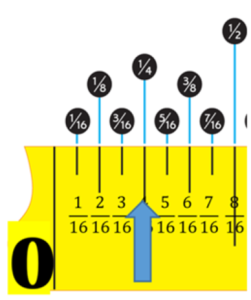
If we then just go halfway along that part of the measuring tape, we get that ½ of ½ is ¼.
We can show ½ of a cup of water in the measuring cup, then get one half of that amount, by pouring out ½ of what we have, which will yield ¼ cup.
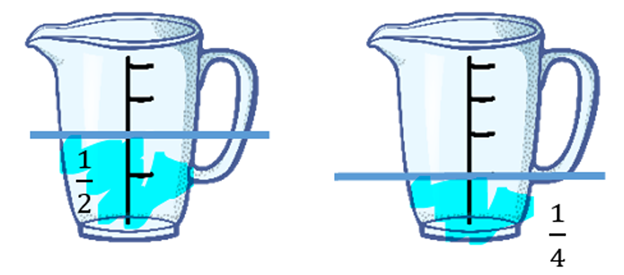
The same idea can also be shown with a piece of paper: fold the paper in half, then fold it in half again, and you have ¼.
Which operation will get us the same result, that ![]() of
of ![]() =
= ![]() ? Would we add the two fractions? Subtract? Multiply? Divide?
? Would we add the two fractions? Subtract? Multiply? Divide?
We know that ![]() , and we know that subtracting the two fractions will give us zero. But if we multiply the fractions, we get our desired answer:
, and we know that subtracting the two fractions will give us zero. But if we multiply the fractions, we get our desired answer: ![]() . Notice that when we multiply fractions, we multiply straight across the tops, straight across the bottoms.
. Notice that when we multiply fractions, we multiply straight across the tops, straight across the bottoms.
Example 5 Demonstrate why 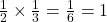 using a piece of paper.
using a piece of paper.
Fold a piece of paper in half, lengthwise, and shade half of it.

Unfold the paper and fold it the other way, in thirds, then shade a third of it.

The part that you shaded twice is 1/6, since it is one piece out of 6.
Multiplication of Fractions Using Repeated Addition or Area
Another way to model fraction multiplication is to use repeated addition. When we multiply 2 × 3 we can show this as 2 rows of three stars, so we can model 2 × 3½ in a similar way.
Example 6 Show why 2 × 3½ = 7 using repeated addition, then draw a picture to illustrate it.
The repeated addition is to add 3½ , twice: 3½ + 3½. Remember that each 3½ is 3 and ½, or 3 + ½. So we get 3½ + 3½ = 3 + ½ + 3 + ½ = 3 + 3 + ½ + ½ = 6 + 1 = 7
Yes, that was a long way to get 2 × 3½! One we have the hang of it, we don’t need to show so many steps, but when we are just starting, the steps can help us see what we are doing better.
We can also show the multiplication with a picture. Here we have 3½ stars, repeated 2 times.
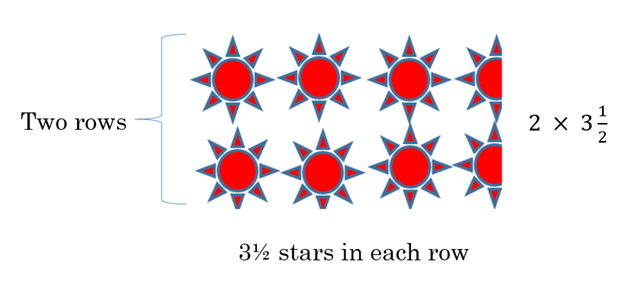
Counting the number of whole stars, we have 6 whole stars. We have 2 half stars, which is the same as 1 whole star. 2 times 3 and a half = 6 whole stars + 2 half stars = 6 stars + 1 star = 7 stars.
We can also draw a 2 by 3½ rectangle. In the picture below, the grid is divided into whole numbers (the dark lines) and quarters, to make drawing easier. The rectangle inside the grid is 2 whole inches going down, and 3½ inches across the top.
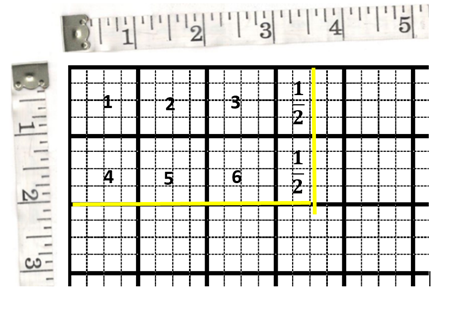
This gives us a total area of 6 whole squares plus two half squares, which is 7.
Multiplication of Fractions Using Partial Products
Example 7 Show the same multiplication as in the previous example using partial products and the distributive property.
![]()
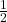 .
.Instead of writing this going across, we can write it vertically, again multiplying 2 times the 1/2, and 2 times 3. Here it’s easier to see if the put the 2 underneath.
![]()
× 2
6+1 = 7
Notice that multiplying 2 × 3½ can done in the same way as multiplying 2 × 3.5. We multiply the 2 by each “part” of the other number.
13.5 (the little 1 shows that “we carry the 1” after multiplying 2 × 0.5 and getting 1)
× 2
7
Kitchen Math
Children can have fun with kitchen math, using measuring cups to help make play dough or food: https://www.youtube.com/watch?v=Yhpiuibv0LY. Want to try this with your own class? Here’s a great recipe for play dough, for 4 to 6 kids, from https://www.iheartnaptime.net/play-dough-recipe/:
- 2 cups all-purpose flour
- 3/4 cup salt
- 4 teaspoons cream of tartar
- 2 cups lukewarm water
- 2 Tablespoons of vegetable oil (coconut oil works too)
- Food coloring, optional
- Quart sized bags
From the website: “Stir together the flour, salt and cream of tartar in a large pot. Next add the water and oil. If you’re only making one color, add in the the color now as well. Cook over medium heat, stirring constantly. Continue stirring until the dough has thickened and begins to form into a ball. Remove from heat and then place inside a gallon sized bag or onto wax paper. Allow to cool slightly and then knead until smooth. If you’re adding colors after, divide the dough into balls (for how many colors you want) and then add the dough into the quart sized bags. Start with about 5 drops of color and add more to brighten it. Knead the dough, while inside the bag so it doesn’t stain your hands. Once it’s all mixed together you’re ready to PLAY.”
If you wanted to make this recipe for 25 kids, how much of each ingredient would you need?
The recipe above is for 4 to 6 kids, so 25 kids is about 5 times as many kids as the recipe calls for. So we would need to multiply each ingredient by 5.
- 2 cups all-purpose flour is easy to multiply by 5: 2 x 5 = 10
- 3/4 cup salt is a bit harder to multiply by 5: 3/4 x 5 = ?
Since 5 is the same as 5/1, we can multiply 3/4 by 5/1, using the same technique of multiplying straight across the tops and straight across the bottoms of the fractions:
![]()
We get 15/4. To see how much this is, divide 15 by 4. You get 3.75 or ![]() . Or you can visually think of fifteen quarter cups:
. Or you can visually think of fifteen quarter cups:
