Sec. 2.7 – Irrational and Rational Numbers, Pi, Multiplying and Dividing Fractions Using Models
Chapter 2, Section 7
Elementary Education – Multiplying and Dividing Fractions Using Models
Math Topics – Irrational and Rational Numbers, Pi
Rational and Irrational Numbers
A rational number is a number that can be written as a ratio, or fraction, using two integers. An irrational number cannot be written as a fraction of two integers. The word irrational comes from the Latin for ir, meaning not, and the word ratio, for fraction. Note: integers are positive or negative whole numbers.

Example 1 Are the numbers 3, 0.5, 0, -4, 0.6666… (also written 0.6̅) and 2√3 rational or irrational numbers? How can we tell?
All of these numbers except the last one are rational.
3 can be written as 3 over 1, that is, ![]() , so it is rational.
, so it is rational.
0.5 is the same as ![]() , so it is rational.
, so it is rational.
0 can be written as 0 divided by any number, for example, ![]() , so it is rational.
, so it is rational.
-4 can be written as -4 over 1, that is, ![]() , so it is rational.
, so it is rational.
Using the methods from the previous section, we ca rewrite 0.6666… as ![]() , so it is rational.
, so it is rational.
Use your calculator to find the value for ![]() = 3.464101615 …. Notice that it does not end and does not repeat, so it cannot be written as a fraction. This number is irrational.
= 3.464101615 …. Notice that it does not end and does not repeat, so it cannot be written as a fraction. This number is irrational.
- Any integer ….-3, -2, -1, 0, 1, 2, … can be written as a fraction over 1, so is rational.
- Any decimal that terminates (ends) can be written as a fraction over a power of 10, so is rational.
- Any decimal that does not end but does repeat can be written as a fraction, using the method we learned in the previous section, so is rational.
- Any decimal that does not end and does not repeat cannot be written as a fraction, so is irrational.
Measuring Circles
The circumference of a circle is the distance all the way around a circle. In the circle below, the circumference is represented by the orange that goes around the outside of the circle, while the dashed line across is the diameter.
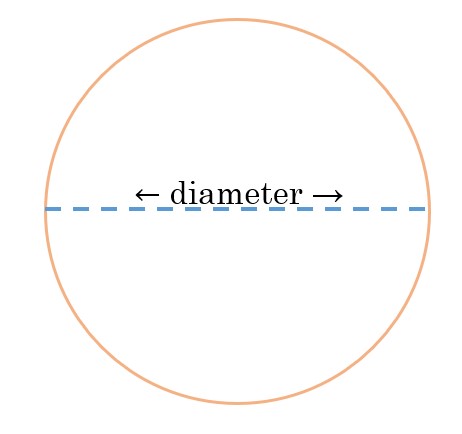
An interesting number arises when we measure these two parts of a circle and then divide them!
Example 2 Measure the circumference and diameter of a circle to the nearest fraction of an inch or using the cm ruler. Divide the circumference by the diameter, C ÷ D. For example, I very carefully measured the top of my coffee cup and got a circumference of 11 inches and a diameter of 3½, so I divide 11 ÷ 3.5 and get 3.14…
Try this yourself with several different circles, large and small. What result do you get every time? What special number is this?
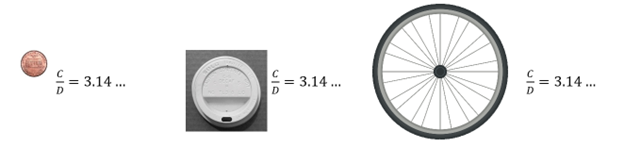
No matter how big or small a circle you have, when you divide the circumference of a circle by the diameter, your answer will always be close to the number 3.14…, or pi. The closer you are to pi depends on how carefully you measured your circle.
The fact that C/D = π is what gives us the formula for the circumference of a circle.
We can see why with a little algebra:
![]()
Multiply both sides of the equation by D:
![]()
D cancels on the left side of the equation and we get ![]() .
.
Since the diameter of a circle is the same as two radiuses, we can also write this as
![]() .
.
Pi, or π, is an irrational number. The decimals of pi go on forever, with no one repeating pattern. There is no way to write pi as a fraction. Some of us learned in grade school to write pi as 22/7, but this quickly diverges (is different from) from pi since 22/7 = 3.1428…, while pi = 3.14159….
Question: Now you try! Which of these numbers: -7, 0, 3π, 1/3, 0.191919…. are rational? Which are irrational? How do you know? Think about it, then click here to check your answers.
Pi (π) Poems
Source: https://en.wikipedia.org/wiki/Piphilology which also has some more great pi poems in all different languages
English
Sir, I tell a rhyme excelling,
In sacred truth and rigid spelling.
Numerical sprites elucidate,
For me the lexicon’s dull weight.
How is this poem related to pi? Hint: count how many letters are in each word!
This more modern version could help you see it:
May I have a large container of coffee, cream and sugar?

What digits do “cream and sugar” add? Does this match the previous poem?
Sir, I tell a rhyme excelling 3. 1 4 1 5 9
“May” and “sir” are both three letters long, then I is 1 letter long and the next word is three letters…. The words in each poem or phrase are each the length of a digit of pi! Pi poems exist in many languages. Below are examples in Spanish, French, and Mandarin.
Spanish
Fue y cayó.
Y queda solamente la inútil cifra
con pocos destinos poderosos,
tristes devenires sin el más sencillo bien.
Idiota, re idiota,
sabe que sus encantos son ya latosos decimales.
Pobre…
Translation
It went and it fell.
And only the useless figure remains,
with little powerful destinies,
sad future without the simplest goodness.
Idiotic, very idiotic,
it knows that its charms are now boring decimals.
Poor [thing]…
The length of each word gives the digits of pi!
French (126 decimal places!!)
Que j’aime à faire apprendre un nombre utile aux sages!
Immortel Archimède, artiste ingénieur,
Qui de ton jugement peut priser la valeur?
Pour moi, ton problème eut de pareils avantages.
Jadis, mystérieux, un problème bloquait
Tout l’admirable procédé, l’œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
Ô quadrature ! vieux tourment du philosophe!
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l’espace plan circulaire?
Former un triangle auquel il équivaudra?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire,
Fonction du rayon. Pas trop ne s’y tiendra:
Dédoublera chaque élément antérieur;
Toujours de l’orbe calculée approchera;
Définira limite ; enfin, l’arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle!
Professeur, enseignez son problème avec zèle!
Translation
How I like to teach this number useful to the wise.
Immortal Archimedes, artist, engineer,
in your opinion who could estimate its value?
For me, your problem had equal advantages.
Long ago, mysterious, a problem blocked
All the honorable process, the great work
That Pythagoras revealed to the Ancient Greeks.
Oh quadrature! Old philosopher’s torment
Unsolvable roundness, for too long you have
Defied Pythagoras and his imitators.
How to integrate the plain circular space?
Form a triangle to which it is equivalent?
New invention: Archimedes will inscribe
Inside a hexagon; will appreciate its area
Function of a ray. Not too much to hold onto there:
Will split each previous element;
Always the calculated orb will approach
Will define the limit; finally, the arc, the limiter
Of this disturbing circle, an enemy too rebellious!
Teacher, teach its problem with zeal!
Chinese
Chinese pi poems are created differently than the previous poems. Instead of each word being a certain number of letters long, they use words that sound like the numbers. For example, in the poem below, the character meaning “mountain” (山 shān) is used to represent the number “three” (三 sān), because shān and sān sound similar. The character meaning “I” (吾 wú) is used to represent the number “five” (五wǔ), and the characters meaning “temple” (寺 sì) and “die” (死 sǐ) are used to represent the number “four” (四 sì).
Some of the mnemonic characters used in this poem don’t work well in Mandarin Chinese, and may work better in a different dialect of Chinese. For example “kill” (殺 shā) for “three” (三 sān), “jug” (壺 hú) for “five” (五 wǔ), “happiness” (樂 lè) for “six” (六 liù) and “eat” (吃 chī) for “seven” (七 qī).
| 山 | 巔 | 一 | 寺 | 一 | 壺 | 酒 |
| Shān | diān | yī | sì | yī | Hú | jiǔ |
| 3 | . | 1 | 4 | 1 | 5 | 9 |
| 爾 | 樂 | 苦 | 煞 | 吾 | ||
| Ěr | lè | kǔ | shā | wú | ||
| 2 | 6 | 5 | 3 | 5 | ||
| 把 | 酒 | 吃 | 酒 | 殺 | 爾 | |
| Bǎ | jiǔ | chī | jiǔ | Shā | ěr | |
| 8 | 9 | 7 | 9 | 3 | 2 | |
| 殺 | 不 | 死 | 樂 | 爾 | 樂 | |
| Shā | bù | sǐ | lè | Ěr | lè | |
| 3 | 8 | 4 | 6 | 2 | 6 |
This can be translated as:
On a mountain top a temple and a jug of wine.
Your happiness makes me so bitter;
Take some wine and drink, the wine will kill you;
If it does not kill you, I will rejoice in your happiness.

Pi Day
On March 14th, many schools celebrate Pi Day, since is March is the 3rd month of the year, so the date is 3/14, like the digits of pi, 3.14…. Here are some great ways schools can celebrate pi day: http://www.teachpi.org/, and here is a fun video: A brief history of pi.
Multiplying and Dividing Fractions Using Models
In the last section, we began to look at models of multiplying fractions. Now we continue by looking at what happens when we multiply two mixed numbers together, and how to model division.
Example 3 Show 2½ × 3½ using a picture and partial products.
Previously, we showed that 2 × 3½
is two rows of 3½ stars. Now, we must repeat the stars 2½ times, so we’ll have another half of a row.
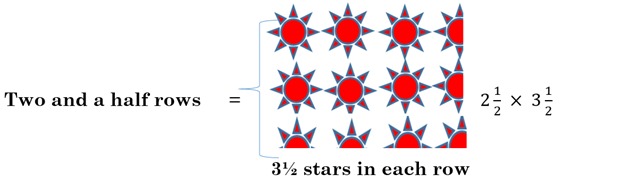
- We have 6 whole stars.
- We have 2 half stars on the right edge ½ + ½ = 1
- We have 3 half stars on the bottom. ½ + ½ + ½ = 1½
- The small part of a star on the bottom right corner is ½ of ½, which is ¼.
![]()
We can also find the answer using the distributive property and partial products:
![]() .
.
This may be easier to see by writing vertically:
![]()
![]()
![]() This line is from multiplying
This line is from multiplying ![]() by each number above it:
by each number above it: ![]() ×
× ![]() , and
, and ![]() × 2
× 2
![]() This line is from multiplying 3 by each number above it.
This line is from multiplying 3 by each number above it.
![]()
Notice that ![]() . Why?
. Why?
Because if I have three half cookies, I have 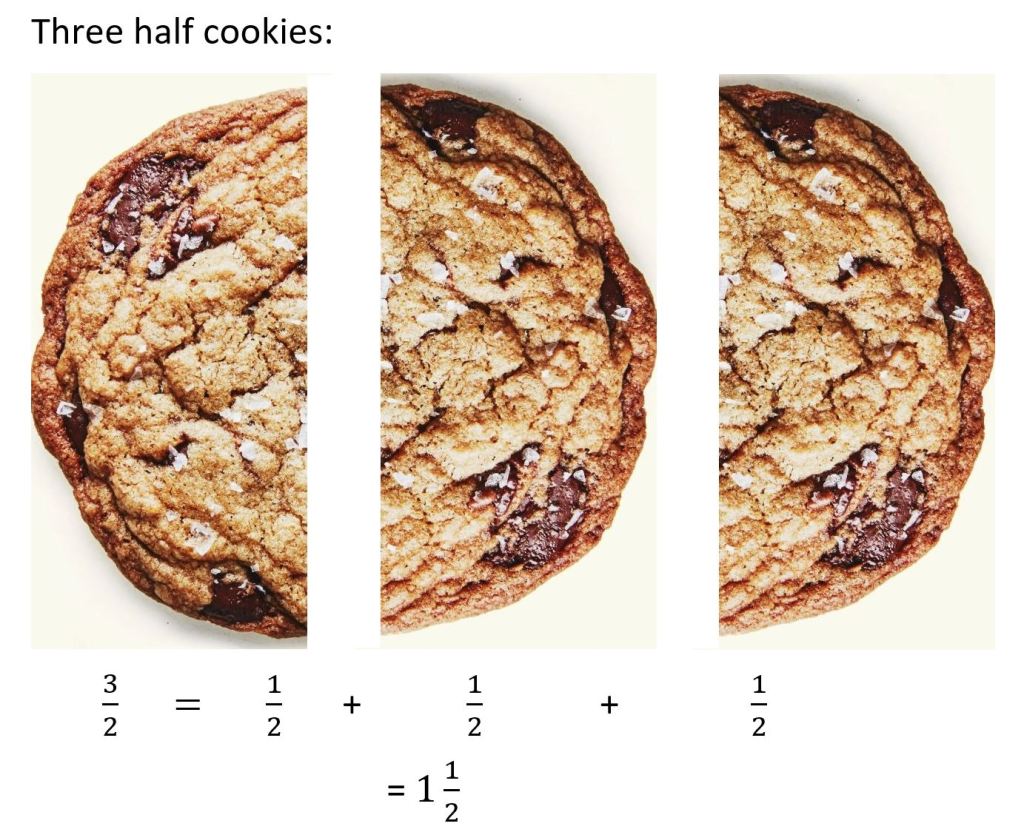
![]() .
.
Two of those half cookies can be put together to make 1 whole, with one of the half cookies left.
![]() .
.
Question: Now you try!
If you multiply 1/2 x 9, what fraction would you get? How could you visualize your answer as cookies to see what mixed number that is? For this question, you can check the answer yourself. Multiply 0.5 x 9 on your calculator to check!
Another way to model multiplication of fractions is using area. Children should already have multiplied whole numbers using area, such as 3 × 2 = 6 using a rectangle that is 3 across and 2 down:
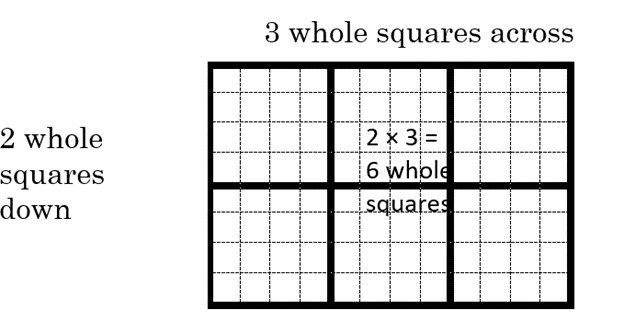
In this picture, the whole squares are also divided into 4 going across, and 4 going down, which we will use in the next example.
Example 4 Show 2½ × 3½ using the area method. Show where you can find each partial product.
To use the area method, draw a rectangle that is 3½ along one side and 2½ along the other:
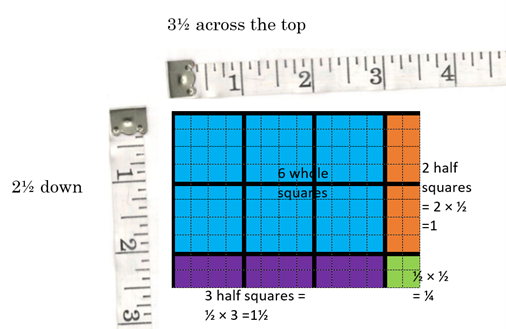
The partial products are 6 whole squares, 2 half squares along the side, 3 half squares along the bottom, and the corner square, ½ × ½ = ¼.
Traditional Methods of Multiplying Fractions
You may remember multiplying mixed numbers by turning them into “improper” fractions:
![]()
To multiply 2½ by 3½ using this method, you must write “two and a half” as “five halves,” and write “three and a half” as “seven halves.” (To see that ![]() , you can think of how many half cookies you have if you have 2 and a half cookies).
, you can think of how many half cookies you have if you have 2 and a half cookies).
Rewriting each mixed number as a fraction and then multiplying may have the advantage of being what you are used to, but there are many steps and some very large numbers, not to mention having to divide 35 by 4 in the end. For kids just learning this, it is important for them to be able to visualize the multiplication, not just follow a procedure.
Division of Fractions Using Objects
One way to think of division is to imagine how many groups fit in. For example, for 15 ÷ 3 we can imagine how many groups of 3 objects can we fit in if we have 15 objects.
How many groups of three hearts can I make from 15 hearts?

Answer: I can make 5 groups. So, 15 ÷ 3 = 5.
Similarly, we can think of 1 ÷ ¼ as how many ¼’s fit in to a whole. Here’s an easier way for you, as a grown up, to imagine this: If I have $1, how many quarters is this?

There are 4 quarters in one dollar, so ![]() . This may help you remember that when you divide, you must “flip the second fraction and multiply,” that is,
. This may help you remember that when you divide, you must “flip the second fraction and multiply,” that is, ![]()
But it’s even better if you understand that the answer should be 4!
Example 5 Show 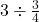 using money.
using money.
Now we have three whole dollars, and we want to see how many groups of three-quarters fit in.

Since ¾ = three quarters, imagine circling groups of three, just as with the hearts.

We can fit in 4 groups of three quarters, so ![]()
To get this arithmetically, we flip the second fraction and multiply: ![]()
Children may not be as facile at using money as adults, so with children, you may want to focus on shapes, such as the hexagon. The next example looks at a similar problem, but now using hexagons.
Example 6 Show 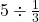 using hexagons.
using hexagons.
For this problem, you will need 5 hexagons, and you want to show how many thirds (![]() ) fit in to them.
) fit in to them.
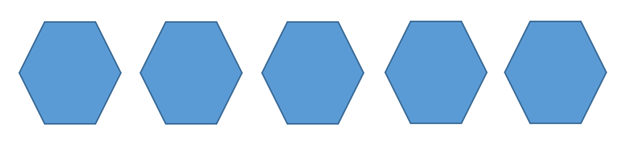
Three rhombuses (diamonds) fit into each hexagon, so a rhombus is ![]() :
:
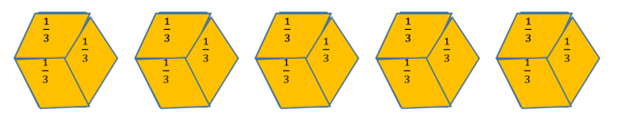
Since we have a total of 15 of these rhombuses (diamonds), this gives us that ![]() .
.
We get the same answer when we “flip” the second fraction and multiply: ![]() . Notice that we also had to write 5 as
. Notice that we also had to write 5 as ![]() so that we could multiply.
so that we could multiply.
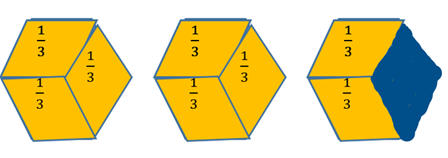
Example 7 Show 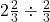 using hexagons.
using hexagons.
We will need to draw two whole hexagons, and part of the next one, then see how many 2/3 fit in to this. Here we have 2 whole hexagons, plus ![]() of a hexagon.
of a hexagon.
Now think about making groups of two-thirds, to get ![]() .
.
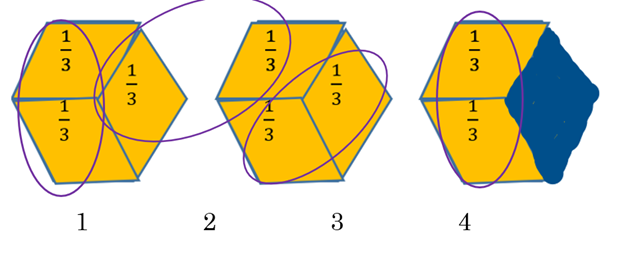
You get four groups of 2/3, so ![]() .
.
To show the same thing using arithmetic, we would have to change the ![]() into
into ![]() , then flip the second fraction and multiply:
, then flip the second fraction and multiply:
![]()
Notice that the arithmetic, if it is new for you, could take longer and be more difficult than drawing a picture and using common sense.
A perfect number is the sum of its proper divisors. How do we translate this statement?
A perfect number
is → =
the sum → add up
of its proper divisors → divisors are numbers that divide into a number. A proper divisor is any divisor except the number itself.
Example 8 Is 6 a perfect number?
The divisors of 6 are 1, 2, 3, and 6. We don’t include 6. The sum of the proper divisors is 1+2+3 = 6, so 6 is a perfect number, since it is equal to the sum of its proper divisors.
Example 9 Is 8 a perfect number?
The divisors of 8 are 1, 2, 4, and 8. We don’t include 8. The sum of the proper divisors is 1+2+4 = 7, not 8, so 8 is not a perfect number.
How do we find the divisors of larger numbers? We can use a factor tree to find all the prime factors, then combine prime factors to find all the divisors.
Example 10 What are the divisors of 60? Is 60 a perfect number?
Since 60 is even, we know that 2 is a divisor of 60. Since 60 ÷ 2 = 30, 30 is another divisor of 60.
3 is another divisor.
Thus, the divisors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
When we find the sum of the proper divisors (everything except 60), we get 1+2+3+4+5+6+10+12+15+20+30 = 108, not 60, so 60 is not a perfect number.
