Sec. 3.2 – Set Operations with Two- and Three-Circle Venn Diagrams
Chapter 3, Section 2
Math Topics – Set Operations with Two- and Three-Circle Venn Diagrams, Introduction to Using Regions, Introduction to DeMorgan’s Laws
Elementary Education – Uses of Sets in Different Subject Areas, Playing “Guess My Rule.”
Elements in Venn Diagrams
Venn Diagrams can be used to explain relationships between different shapes, types of numbers, even between animals or the kinds of foods we like! In this section, we’ll look at two fun examples, which we will use to practice and dig more deeply into the ideas from the previous section. We’ll also see how to use regions to help us see what parts of the Venn diagram to use.
Before we start, we introduce one new symbol.
- ∈ means “is an element of,” meaning it is an object in the set.
- If we put a line through the symbol, ∉, then it means, “is not an element of.”
For example, if I have set A = the multiples of 2 between 1 and 10 = {2, 4, 6, 8, 10}, then it is true that 4 ∈ A. We read that as, “4 is an element of A.” It is also true that 5 ∉ A. We read that as, “5 is not an element of A.”
For our next examples, instead of multiples of numbers, let’s look at other things that can be organized using sets. This will help us review the concepts from the previous section, before we look at Venn Diagrams with three circles.
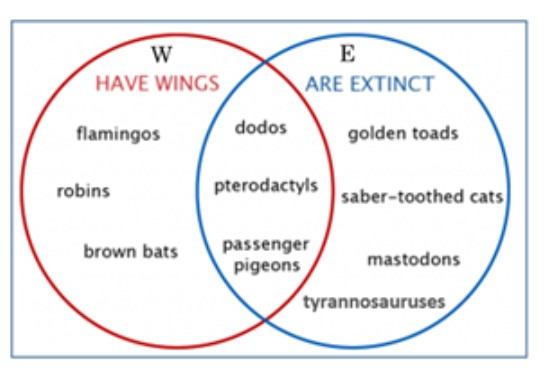
Types of animals can be organized into a Venn diagram, as below.
Example 1 Name an animal that is in W and use the correct symbol to write it. Name an animal that is not in W and use the correct symbol to write it.
We can write flamingos ∈ W, which means, “Flamingos is an element of W.”
We can write golden toads ∉ W, which means, “Golden toads is not an element of W.”
What about dodos? Are they an element of W, or not?
Yes, dodos are an element of W, too, since dodos have wings. We can write dodos ∈ W. Remember that W is the whole circle, even the part that overlaps with set E.
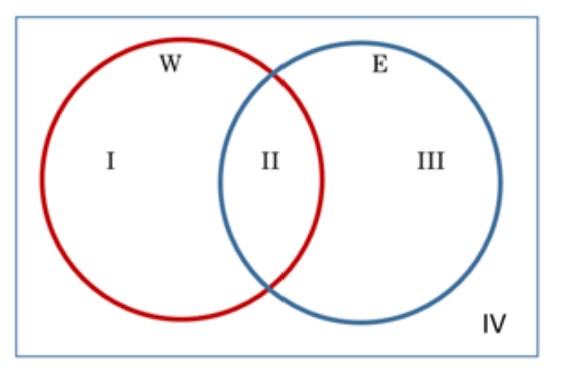
Numbered Regions for Two-circle Venn Diagrams
The Two-circle Venn Diagram has four major regions, numbered below using Roman numerals I to IV.
I = 1, II = 2, III = 3, and IV = 4. We use Roman numbers for regions to distinguish them from elements in the set.
- Set W is regions I and II.
- Set E is regions II and III.
- The Universal set is all the regions, I, II, III and IV.
For the next examples, it can be helpful to look at both pictures, showing the elements (picture on the left) and the regions (picture on the right) as we answer this question.
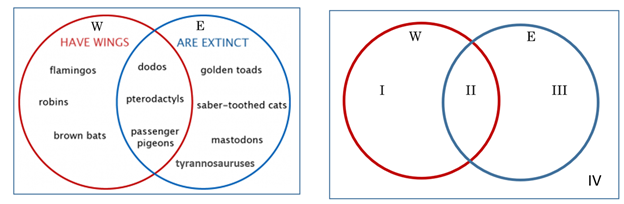
Example 2 How would you say W| in words? What regions describe W| ? What elements are in W| ?
From the previous section, we can recall that the mark after the W means the complement of W, or everything not in W, so we would say, “All animals that do not have wings.” This part of the diagram would be regions III and IV.
To list the elements, we write W| = {golden toads, saber-toothed cats, mastodons, tyrannosauruses}. In this particular example, there was no element in region IV, but if there were, we would include it in our list of elements in W| .
Example 3 Find the intersection and union of the two sets. How would you describe these animals in words? Which numbered region or regions describe the intersection? The union?
In this diagram, the intersection describes all the animals that have wings and are extinct. We write W ∩ E = {dodos, pterodactyls, passenger pigeons}. These are the animals in the overlap of the two circles, region II.
The union is the animals that have wings or are extinct. W ∪ E = {flamingos, robins, brown bats, dodos, pterodactyls, passenger pigeons, golden toads, saber-toothed cats, mastodons, tyrannosauruses.} The union is all of both sets, regions I, II and III.
Remember: the symbol for intersection, ∩ , looks like an n. The word intersection has the letter n in it, as does and! So the intersection of two sets will always be translated as the word and. Union starts with the letter U, and the union symbol, ∪, looks like a U. The union symbol will always be translated as the word, or.
Example 4 How can we describe elements that are in one set but not the other, using set notation? For instance, how can we describe region I, all by itself?
From the previous section, remember the strategy of translating each symbol and letter into words. Think how we would describe flamingos: they have wings, and (but) they are not extinct. Which symbols correspond to and and to not? How would we say that flamingos are an element of this set?
Think about it and try it before you scroll down to see!
Question: Now you try! Now see if you can do this with another animal on the diagram. For example, where are golden toads? Use the words to write the symbols using set notation. Check here to see if you are correct.
Example 5 What about (W ∪ E)|, with the complement symbol outside the parenthesis? What region or regions would that be? Remember that the ( ) groups W ∪ E together, so we take the complement of what we get for W ∪ E. You can think of this as the “order of operations” for sets, just like in algebra. First, we look at the union of W with E, then (W ∪ E)| is outside that — everything that is not in the union of both sets.
What region is outside the union of both sets? Try coloring it to see, or list the regions that are in W ∪ E. The regions in W ∪ E are I, II and III. What is outside those regions?
This would be region IV.
Caution: Sometimes people say that region IV is the universal set, U, but that’s not true. We can see from this example that region IV is what is outside the two circles. But the Universal set, U, is all the regions. U = I, II, III, IV.
What concepts could you explain in your own classroom using Venn diagrams? In elementary school, you would probably not use all the set notation we used, above, but you could use Venn diagrams as a way to organize ideas and to categorize things, just as we did with things that are extinct and things that have wings.
The game of Set (https://www.setgame.com/set/puzzle) is also a fun way to explore categorizing things. It can be lots of fun to play with kids or grownups — but I’ve found that kids are usually better at it than grown ups!
It can also be fun to use the Set cards to play a different game, “Guess My Rule”! Can you guess the rule for set A, below? What about for set B? What kinds of cards would go in the intersection of the two sets? What kinds of cards are outside both sets?
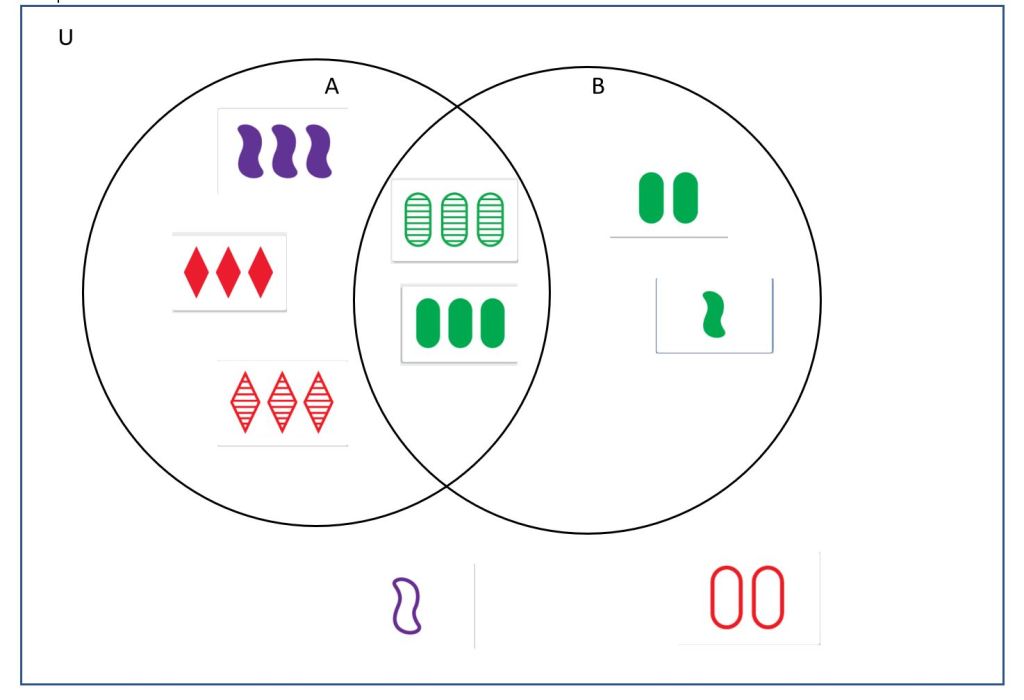
Question: now you try! See if your guesses for each of the above circles are correct, here.
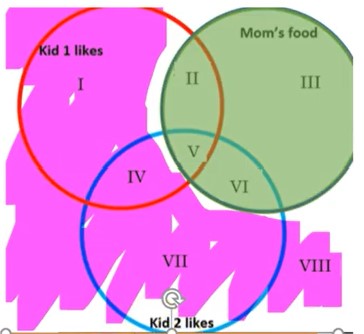
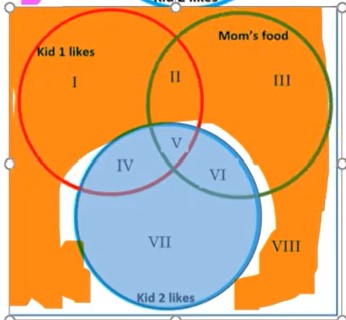
Numbered Regions for Three-circle Venn Diagrams
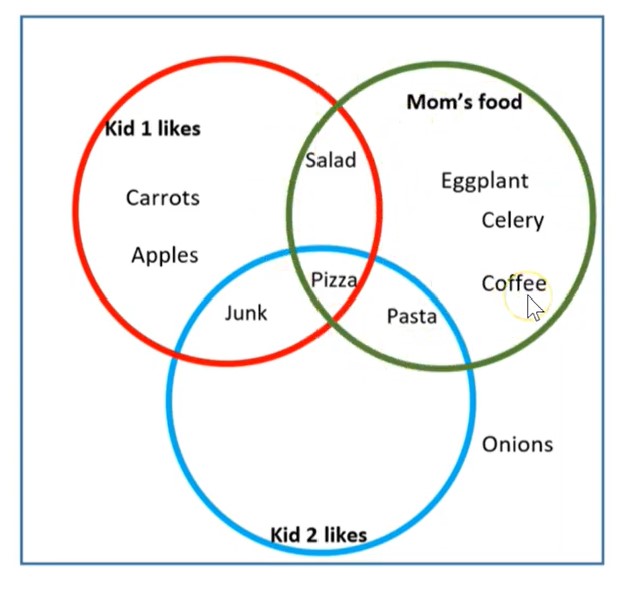
Kid 1, kid 2, and mom don’t have many foods in common! This make me think of my son. Is this true in your family, too?
We will use this diagram to examine the intersection and union of all three sets and of just two of the sets, and more about the complement of a set. Notice that with three circles, we have many more regions to consider than with just two sets.
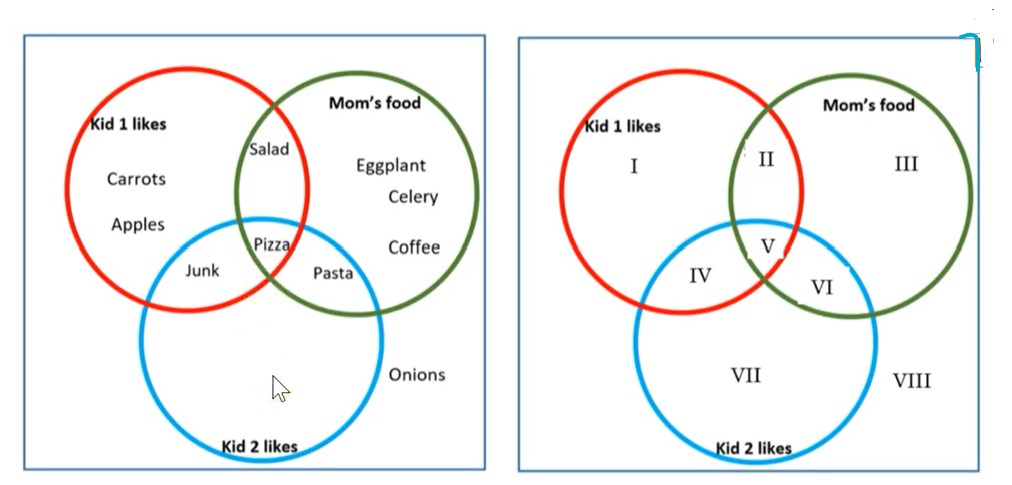
Note: I = 1, II = 2, III = 3, IV = 4 , V=5, VI= 6, VII = 7, VIII = 8
Example 6 Why is pizza in the middle of all three circles?
It’s the one food all three of them like! Pizza is in the intersection of all three of the sets, K1 ∩ K2 ∩ M. This is food liked by kid 1 and kid 2 and mom. Remember that intersection translates as the word and. The intersection of all three sets is region V (the Roman numeral for 5).
Example 7 What kind of food is in K1 ∩ M? This is the intersection of the two sets, where they overlap. It’s the food that kid 1 and mom like.
K1 ∩ M = {Salad, Pizza}
Caution: the intersection of K1 and M is not just the salad; both the pizza and the salad are in the overlap. Look at where all of the red (K1) circle and all of the green (mom) circle overlap. It does not matter whether it also overlaps with K2. The food that is liked by kid 1 and mom could have kid 2 food in it!
Imagine shading in the whole kid 1 circle in red, and the whole mom circle in green:
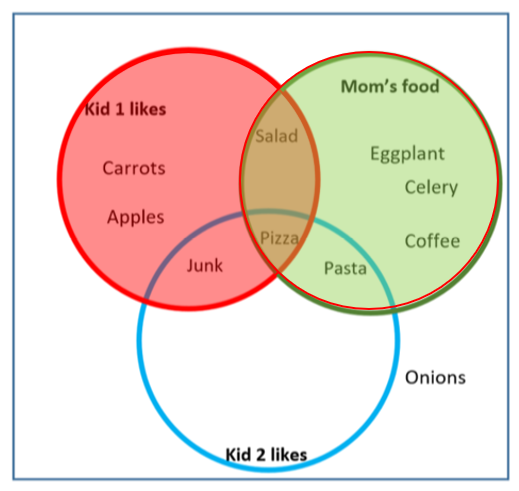
The part that is shaded with both colors (red and green) is the intersection.
Looking at the regions, K1 ∩ M = regions II and V.
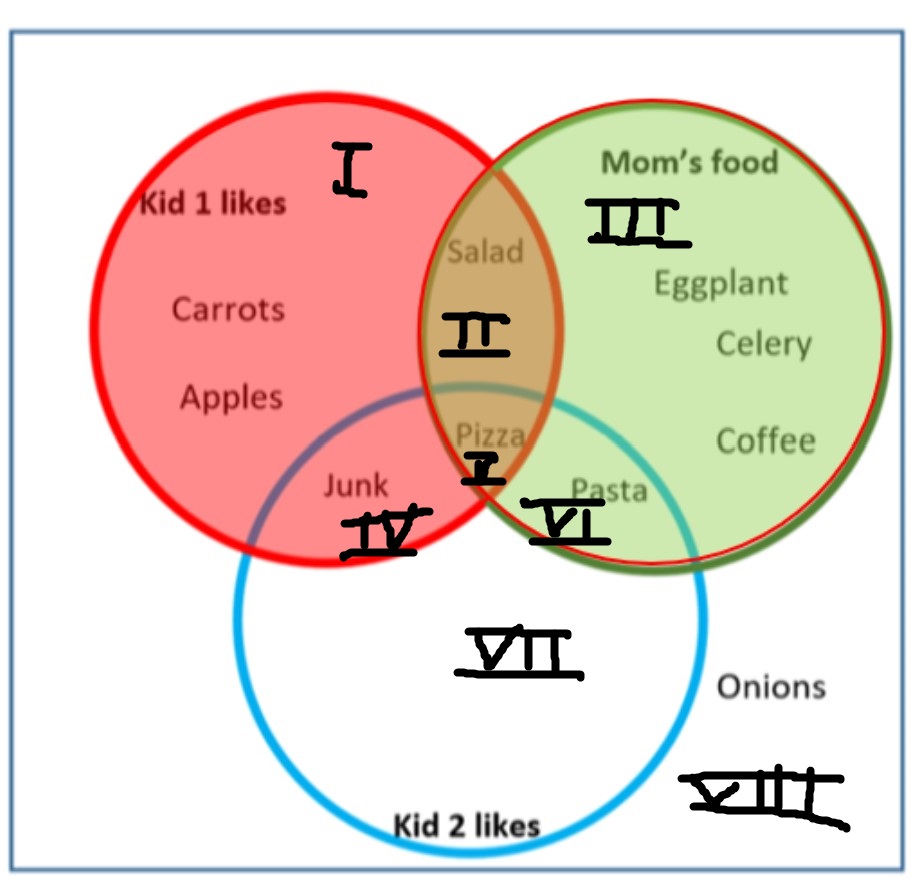
Example 8 What kind of food is in K1 ∪ M? This is Food liked by K1 or mom. This is the union of the two sets.
K1 ∪ M = {Carrots, Apples, Junk, Salad, Pizza, Eggplant, Celery, Coffee, and Pasta} It is any part of the diagram that is colored in either color above (red or green). Using the regions, K1 ∪ M = I, II, III, IV, V and VI.
Example 9 How would you find M| , and how would you write this in words? Recall from the previous section that M| is the complement of M, which is everything that is not in M. This means anything outside the Mom’s food circle. Block off the M circle (colored in green) and you will find that what’s left.
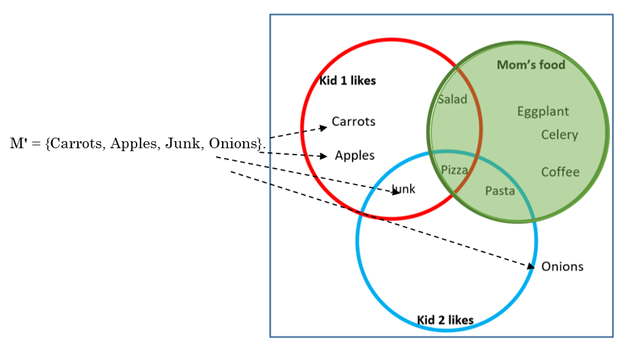
In words, we write, the foods that mom does not like. M| = {Carrots, Apples, Junk, Onions}.
Notice we don’t need to talk about K1 or K2 when we translate the complement into words. We just directly translate what we see in the symbols, M| = not food that Mom likes.
Example 10 What about (M ∪ K2)| ? What foods are these, and how would we describe this set in words? To find these foods, look first at M ∪ K2. Imagine blocking off all of that in yellow. What’s left is the complement, what’s not colored in yellow.
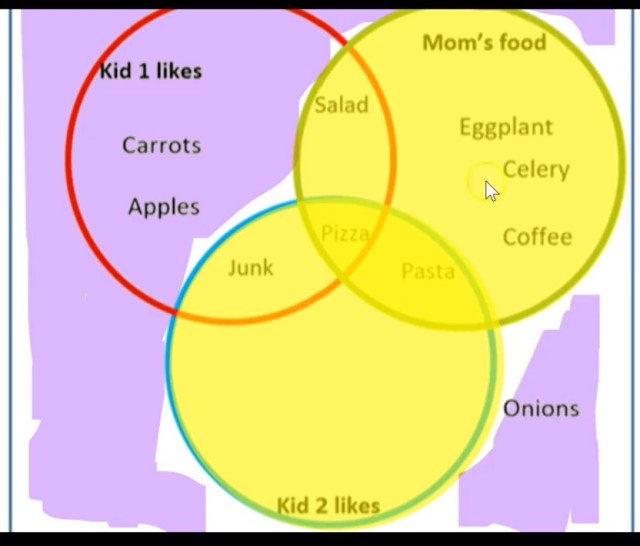
(M ∪ K2)| = {Carrots, Apples, Onions}, regions I and VIII.
In words, this is the food that is not liked by mom or kid 2.
Notice:
- We translate the words using only the set M and the set K2. We don’t need to mention K1 or the part outside all the sets – both these parts are taken care of, just by saying not liked by mom or kid 2.
- We only use one not, since there is only one not symbol.
DeMorgan’s laws

I do not like Coke or Pepsi. This is true. I hate the sugar, but even the taste, ugh. I don’t much like the diet stuff either. I just do not like Coke and I do not like Pepsi.
Reread those sentences and watch what happens to the or, the not and the and!
Here’s what this looks like symbolically:
(C ∪ P)| = I do not like Coke or Pepsi,
C| ∩ P| = I do not like Coke and I do not like Pepsi.
The above is an example of DeMorgan’s Laws. Notice how the not symbol changes from one to two places, and how the or changes to and !
DeMorgan’s Laws*
(A ∪ B)| = A| ∩ B|
(A ∩ B)| = A| ∪ B|
Notice:
- In each example, the ∪ or ∩ gets turned upside down.
- In each example, the not symbol, |, goes from being one symbol outside the parenthesis to being a symbol on each letter. This is similar to the way we distribute a negative in algebra, for example,

*Remember him? That’s the mathematician, Augustus DeMorgan, from our problem solving unit, who said, “I was x years old in the year x2.” Yes, he really was an actual mathematician living in the 1800’s!
Example 11 Use DeMorgan’s laws to rewrite (M ∪ K2)| from example 12, using the symbols. Then translate your new symbols into words. See if it makes sense, using words, that the two sets are the same, then we will look at the results using the Venn diagrams.
(M ∪ K2)| = M| ∩ K2|
In words: food that is not liked by mom or kid 2 becomes food that is not liked by mom and is not liked by K2.
Notice that the symbol changes from or to and (turns upside down) and the not gets “distributed” to each set inside the parenthesis.
In our Venn Diagram, we previously found (M ∪ K2)| by shading everything that was not in the union of M with K2. To be totally clear, I have colored this area in light purple, below. The regions in purple are regions I and VIII.
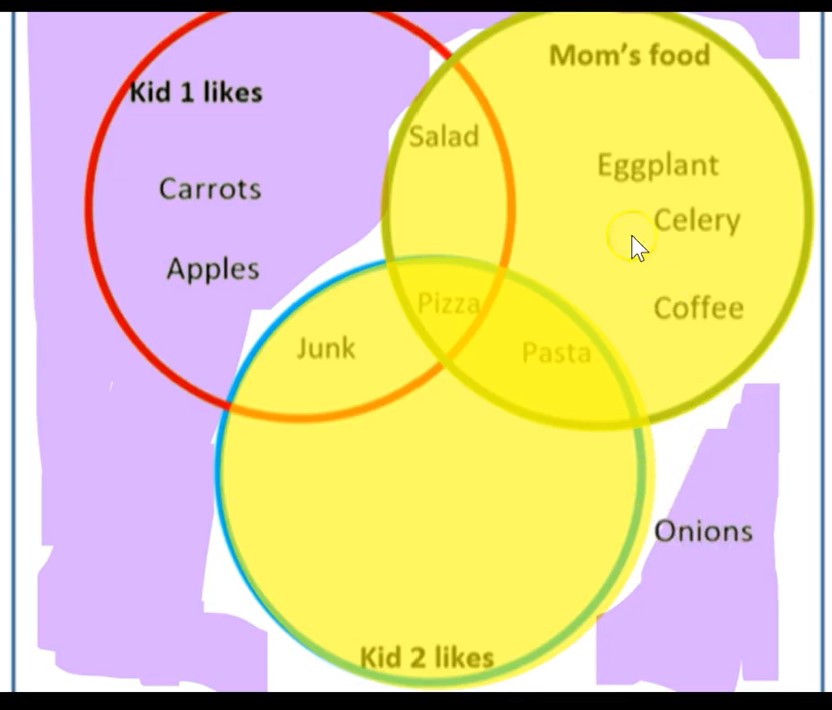
Now we’ll look at how to find M| ∩ K2| using the Venn Diagram, with both coloring and regions, to show that it comes out to the same purple area as above.
Step 1: we find M| on the diagram. This is everything that is not in M, so everything that is not shaded in green. For clarity, I will color that area in pink. Or, if you don’t want to shade, you can write down the regions: M| = regions I, IV, VII and VIII.
Step 2: Find K2| on the diagram. This is everything that is not in K2, so everything that is not blue. For clarity, I will color that area in orange. Or, if you don’t want to shade, you can write down the regions: K2| = regions I, II, III, and VIII.
M| ∩ K2| is the intersection, or overlap, of these two pictures. It is what has been colored in both pink and orange. You can also think of it as the regions that are in both M| and in K2|. The regions we colored pink for M| were I, IV, VII and VIII. The regions we colored orange for K2| were I, II, III, and VIII. So, the regions that got colored both colors were I and VIII.
As you can see, this is the same shaded area as before, for (M ∪ K2)| !
Thus, we have shown that (M ∪ K2)| = M| ∩ K2|.