Chapter 3, Section 3

Math Topics – More Set Operations with Three Circle Venn Diagrams, Using Regions with Three Set Diagrams, More on DeMorgan’s Laws

Elementary Education – Guess My Rule; Common Factors and Multiples

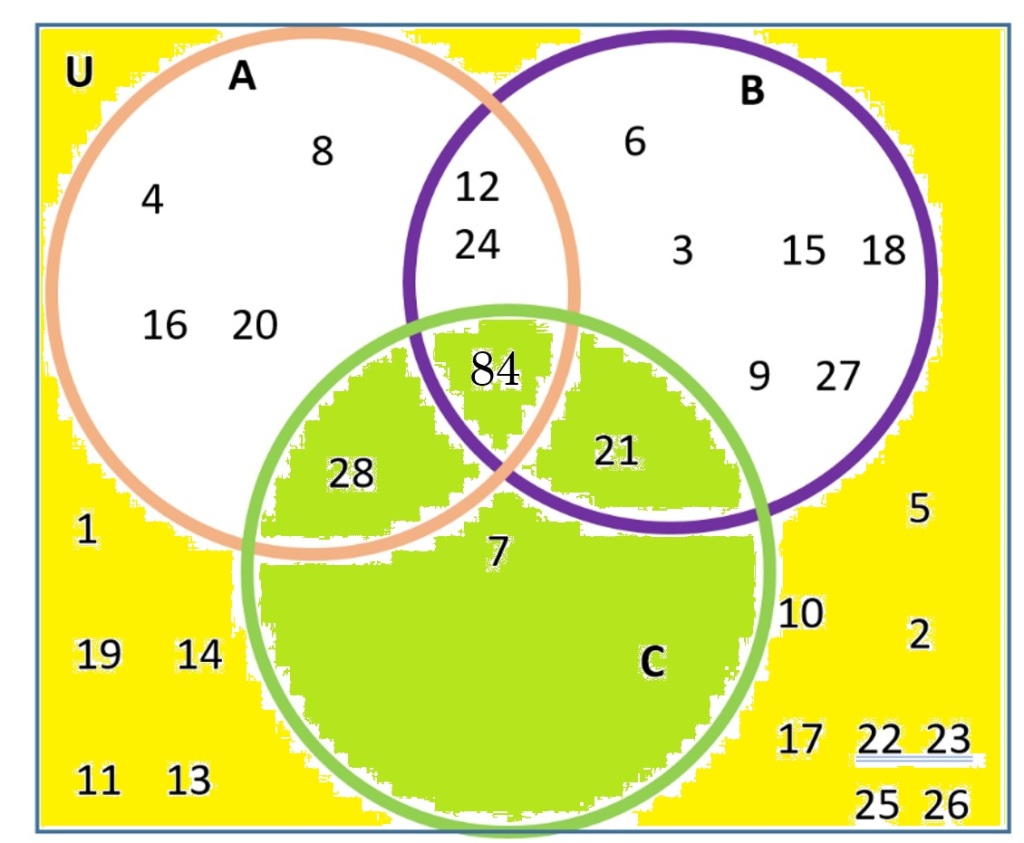
Remember the game of Set ? Here’s another “Guess My Rule” using those cards.

Example 1 Guess My Rule with Three Sets

What type of card is in each set? Can you guess the rule? What kind of card is in the intersection of all three of these sets? Try to guess before you scroll down to see the answers!

The set on the left (circled in green) is cards that each have two shapes on it.

The top set is cards with ovals.

The bottom right set is cards that are red.

The middle is the intersection of all three sets: cards that have two shapes and are oval and are red (a red card with 2 ovals). The word intersection translates to and.

Example 2: GCF Here’s a Guess My Rule that might be particularly challenging, even though it only has two sets! Hint: think of factors, not multiples! What kinds of numbers are in the intersection?

What are all the numbers in set A factors of?

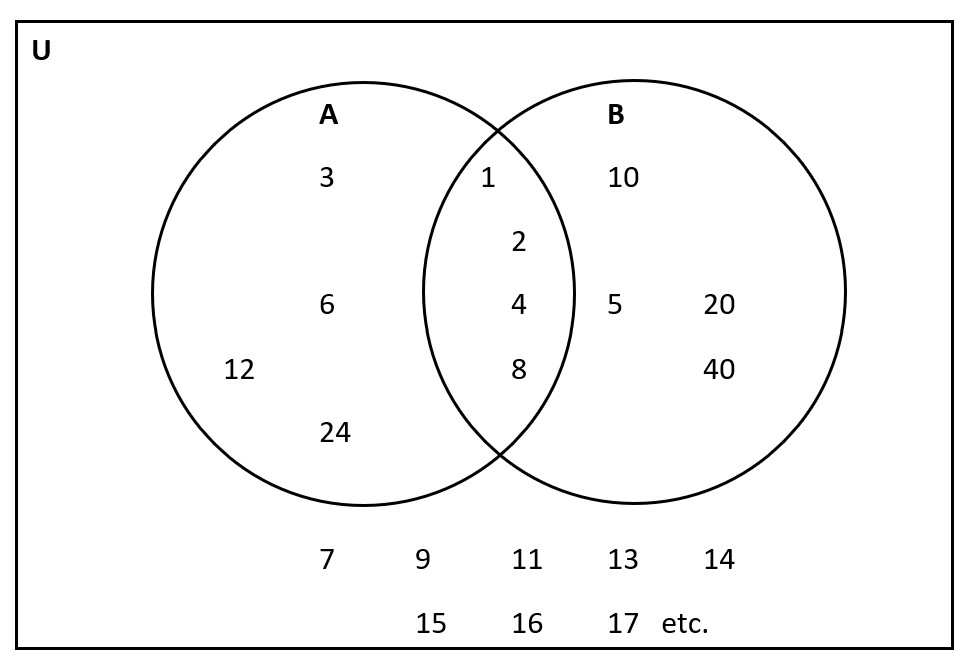
What are all the numbers in set B factors of?

What are the numbers in the middle?

A = the factors of 24 = {1, 2, 3, 4, 6, 8, 12, 24}

B = the factors of 40 = {1, 2, 4, 5, 8, 10, 20, 40}

The numbers in the intersection are the factors of both 24 and 40.

A ∩ B = {1, 2, 4, 8}

Sets can be a great way to visualize common factors, including the greatest common factor, or GCF. The greatest common factor is the largest number both sets have in common. This is the largest number in A ∩ B.

A ∩ B = {1, 2, 4, 8} The largest number in this set is 8. Thus, the GCF of 24 and 40 is 8.

We can use the GCF when we simplify fractions. For example, to simplify 24/40, we can divide both top and bottom by 8, the GCF, which will simplify the fraction completely:

It is also fine to simplify the above fraction more slowly, by dividing by one of the smaller common factors in our set, like 2 or 4, then dividing by 2 again until you are done. It is better to go more slowly and thoughtfully if it helps you to understand what you are doing.

Example 3: LCM See if you can guess the rule for each of the sets below. After that, see what number you can find that could go in the intersection of all three sets. Hint: now we are back to multiples!

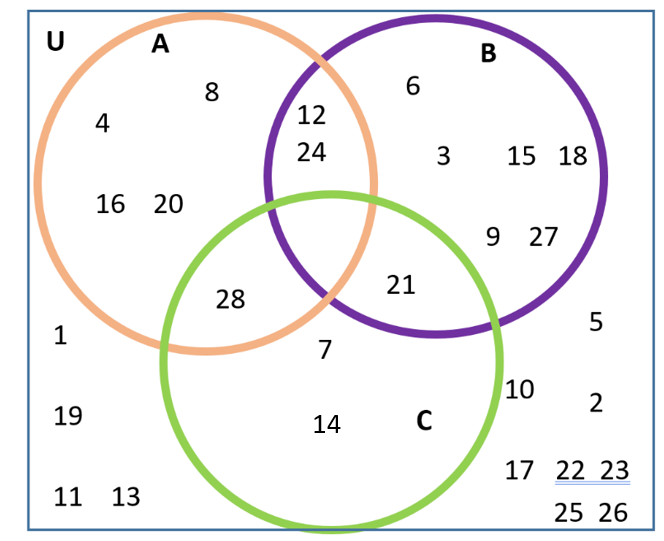
U = the numbers from 1 to 28

A = the multiples of 4

B = the multiples of 3

C = the multiples of 7

Right now, the intersection of all three sets has nothing in it. That is, A ∩ B ∩ C = ∅, the empty set.

Think about what number could go in the intersection of all three sets, if we made the universal set bigger. Can you think of more than one possibility?

If we made the universal set bigger, a number that could go in the intersection of all three sets A ∩ B ∩ C would be a multiple of 4 and a multiple of 3 and a multiple of 7. We can get that common multiple by multiplying all three numbers: 4 × 3 × 7 = 84

Other possible numbers that would also work are the larger multiples of the three numbers, for example, ( 4 × 3 × 7 ) × 2 = 84 × 2 = 168 could also go in the middle of the three sets; 84 × any number would be in the intersection of all three sets.

Multiplying gets us larger common multiples. The least common multiple (LCM) of three numbers is the smallest multiple of all three numbers. In this particular case, the LCM is 84.

The LCM is often used when adding fractions with unlike denominators. For example, to add 2/3 + 1/4 + 5/7

we use the LCM 84, which will become the common denominator of the three fractions. It is also fine to use a larger common denominator – the answer will still simplify to be the same as above.

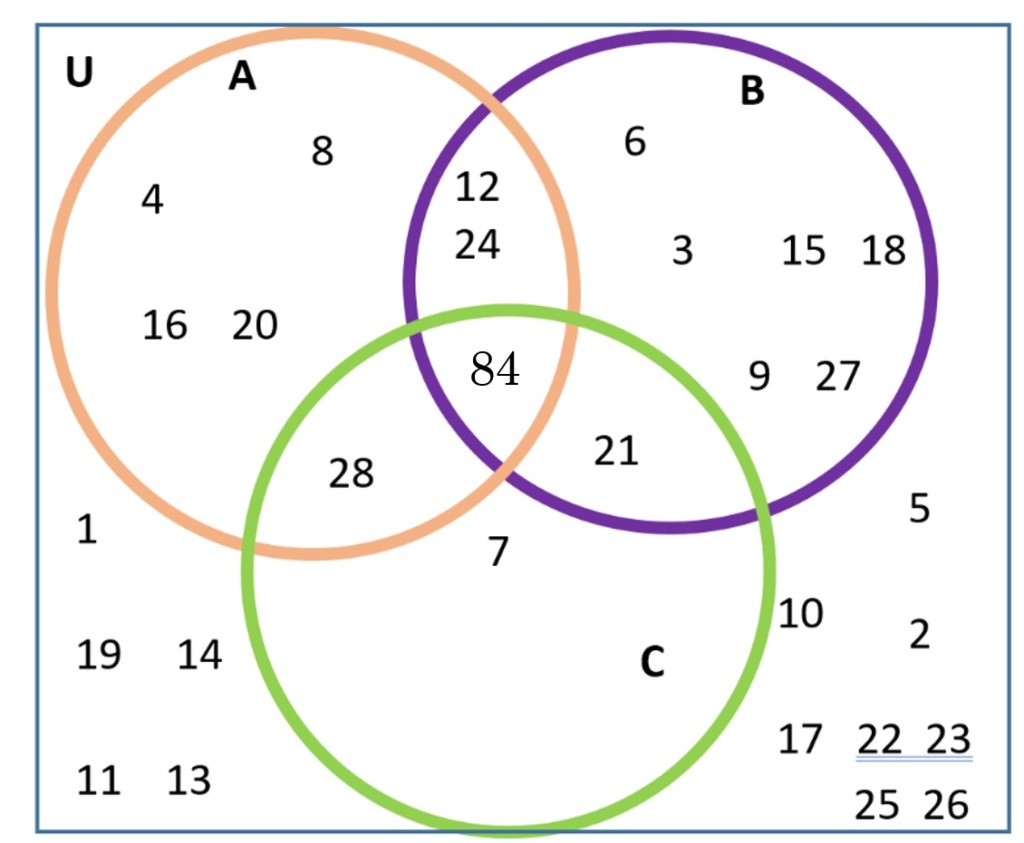
Example 4 Using the three sets from the previous example, with our new number 84 added in, find (A^| ∩ C) ∩ B and translate into words.

We will practice the three three methods from section 3.1 so that you can use three different ways of understanding; this is similar to how you will want to teach your students using multiple modalities.

Verbal Method

To find (A^| ∩ C) ∩ B in words, translate each individual symbol:

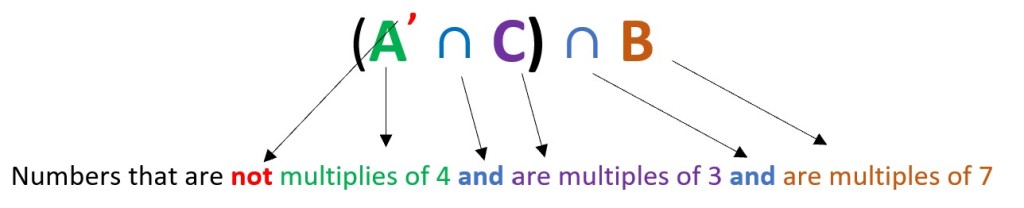
Using just the words, can you tell which number in the diagram fits this description? It must be a number that is not a multiple of 4 but is a multiple of 7 and also is a multiple of 3. Look back at the diagram, and see if you can tell. Write the number down — we will come back to it after we have done another method, to see if you were correct!

Visual and List Method

Just as with algebra, there is an order of operations for sets.

Order of Operations for Sets

• First, find the area or elements for anything inside parenthesis. Start with any set that has a complement (not) symbol ( ‘ ) first.
• Next, take care of any complement outside the parenthesis.
• Finally, take the intersection or union of what was in parenthesis with anything outside.

First, find (A^| ∩ C), inside parenthesis.

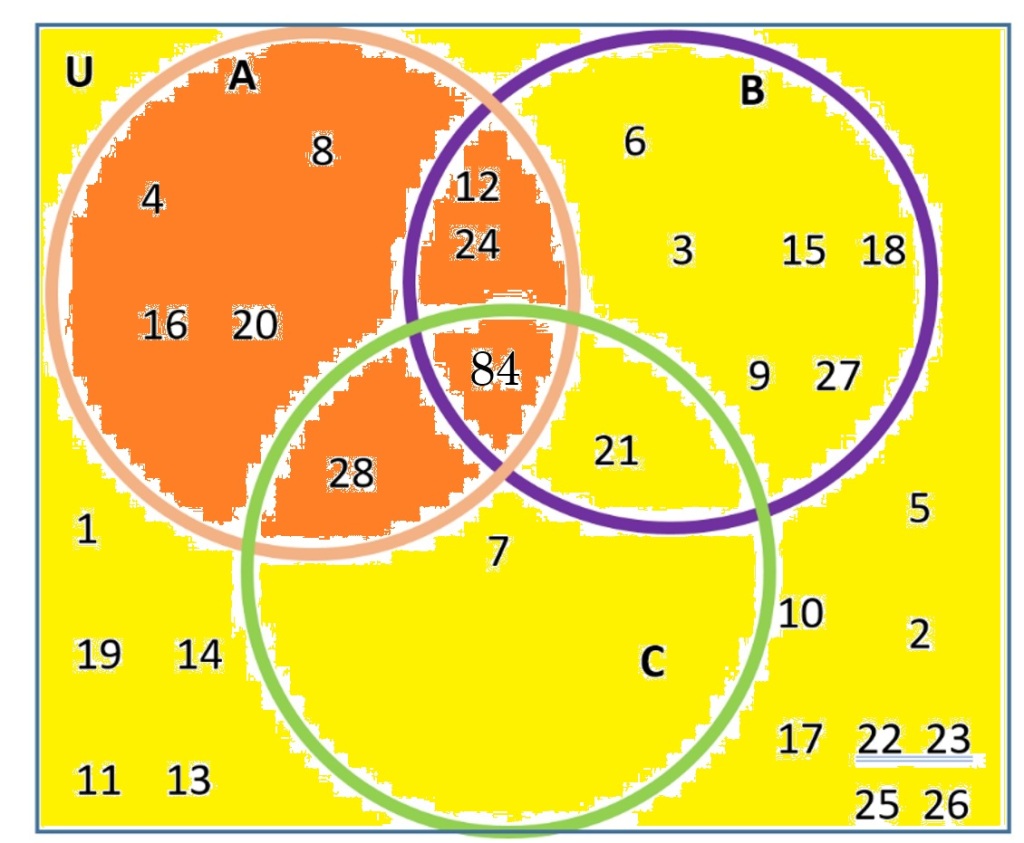
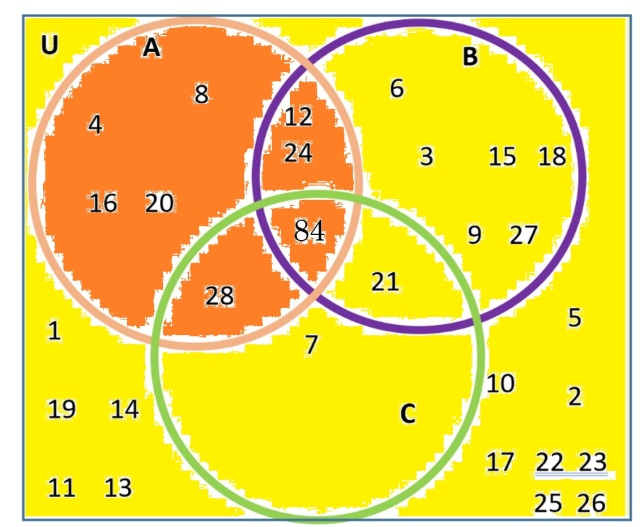
Begin with A^|, the complement. Think of all the numbers not in A, that is, all the numbers that are in the Universal set that are not multiples of 4. Visually, we block off A in the diagram, and the complement is the numbers that remain.

A^| = Everything that is not in A = everything that is not colored orange = everything that is colored in yellow

It can be helpful to write the regions if you don’t have a colored pencil or highlighter.

The regions for A are I, II, IV, V, so the regions A^| are the rest of them, regions III, VI, VII, VIII. Notice that we are combining the visual with making a list of the regions.

Next, we want to find where that yellow area intersects with C. Remember, we are finding (A^| ∩ C) ∩ B by first finding (A^| ∩ C).

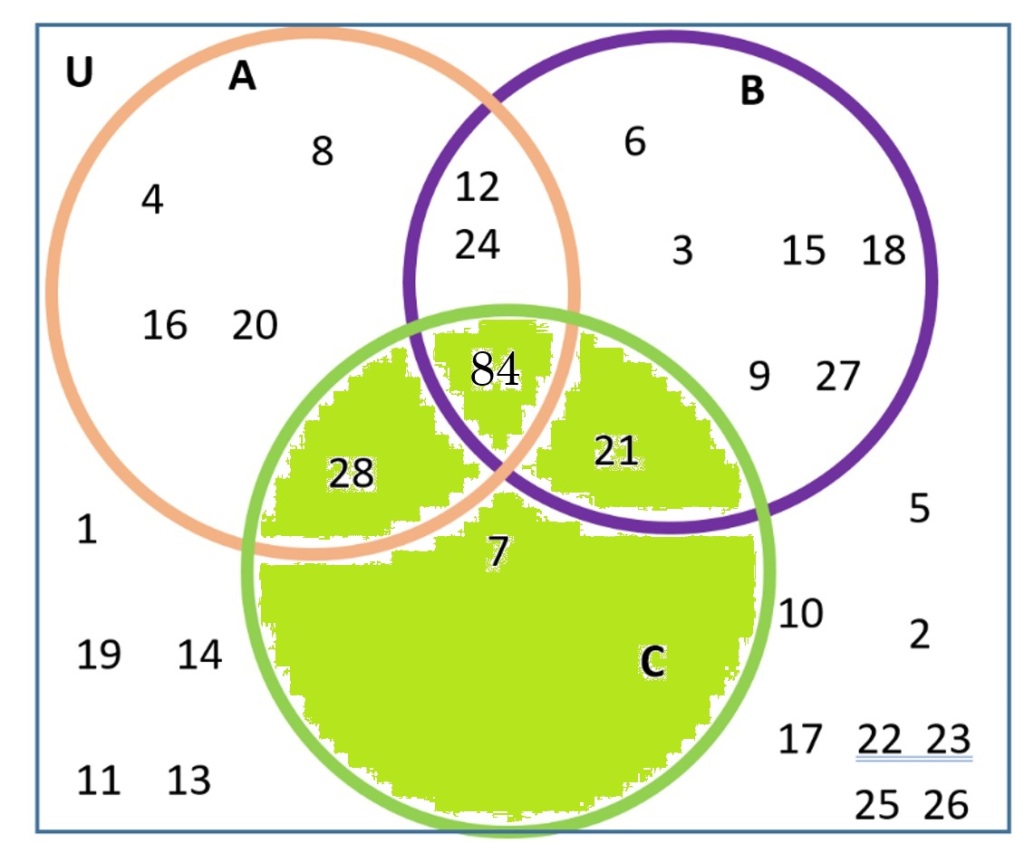
Set C is the area colored in green, regions IV, V, VI and VII.

To find A^| ∩ C, find the overlap between the two colorings – find what has been colored in yellow and in green. Below shows a side-by-side of what you colored in yellow and green, so you can see what you colored both colors.

You might find it easier to see with the regions you listed:

A^| = yellow regions III, VI, VII, VIII

C = green regions IV, V, VI and VII.

Regions you colored both yellow and green = VI and VII. These are the two regions you see on both lists (the overlap of the two lists).

The pink area below shows A^| ∩ C, regions VI and VII.

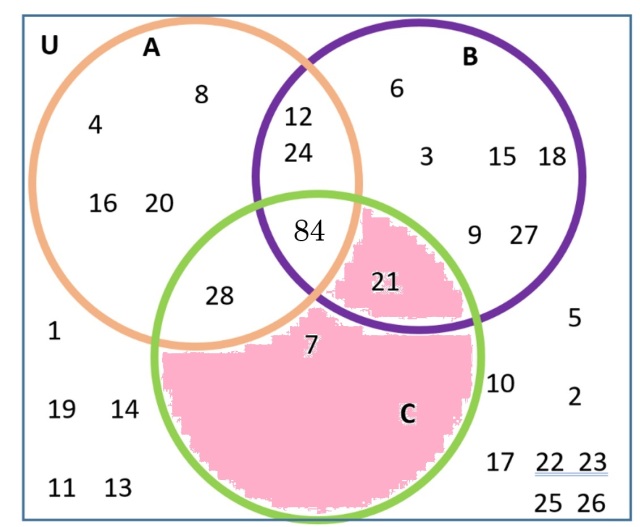
Now we are ready for the last step. We have found (A^| ∩ C). Now, to get the final answer for (A^| ∩ C) ∩ B, we want to find where the pink area,
(A^| ∩ C), overlaps with set B. Set B is colored in blue, below.

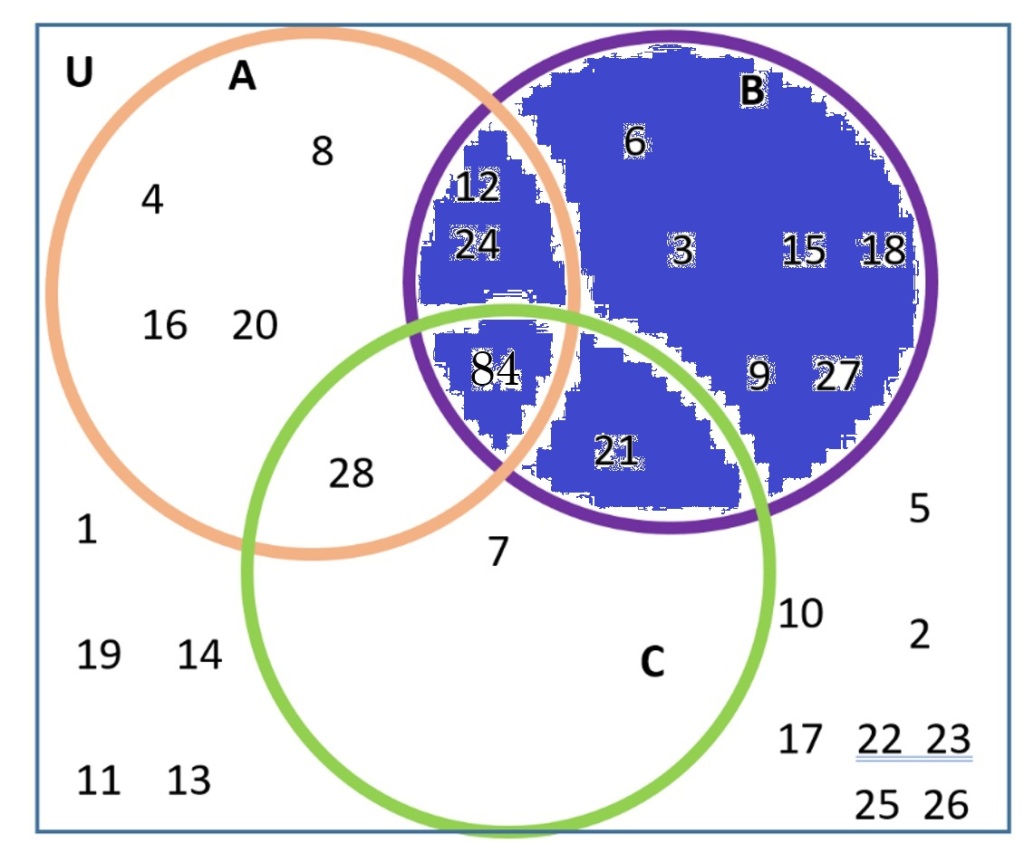
B = regions II, III, V, VI.

A^| ∩ C = regions VI and VII

What region do the two lists have in common? Where do your two colors overlap?

The pink and blue areas overlap in just one region, region VI. This region just has the number 21. Thus,

(A^| ∩ C) ∩ B = {21}

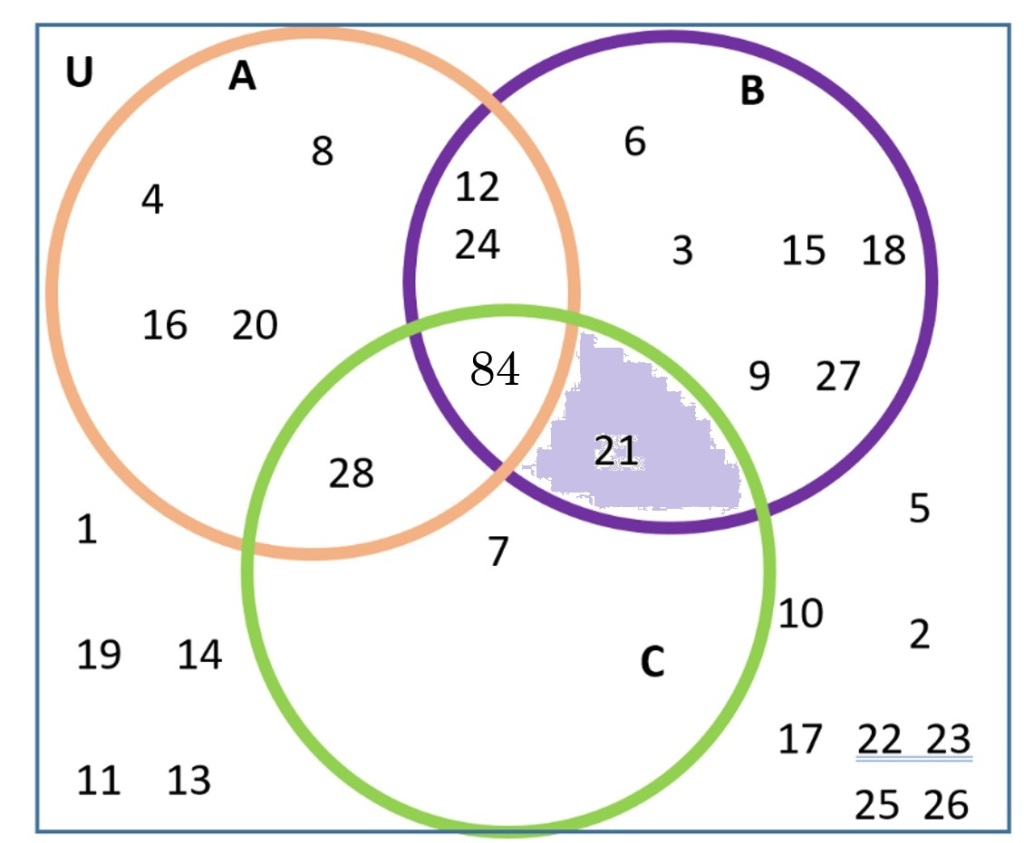
Is this the same answer you found using method 1? The number 21 is the only number that is not a multiple of 4 but is a multiple of 7 and is a multiple of 3!

For those who learn best visually, the method of shading can work really well, and after a while, it’s possible to imagine the areas, without having to actually color them. But it’s also fine to keep coloring them! For others, it easier to have a list method, or algorithmic approach to solving sets problems. An algorithmic approach means being able to follow a set of rules or steps to get to the answer (as we often do in algebra).

Example 5 Using the same sets, find (A ∪ B)^| ∪ C.

This time we’ll try the visual method first.

First, find A ∪ B, the inside of the parenthesis. This is the union, all of A with B. In the picture below, A ∪ B is colored in green.

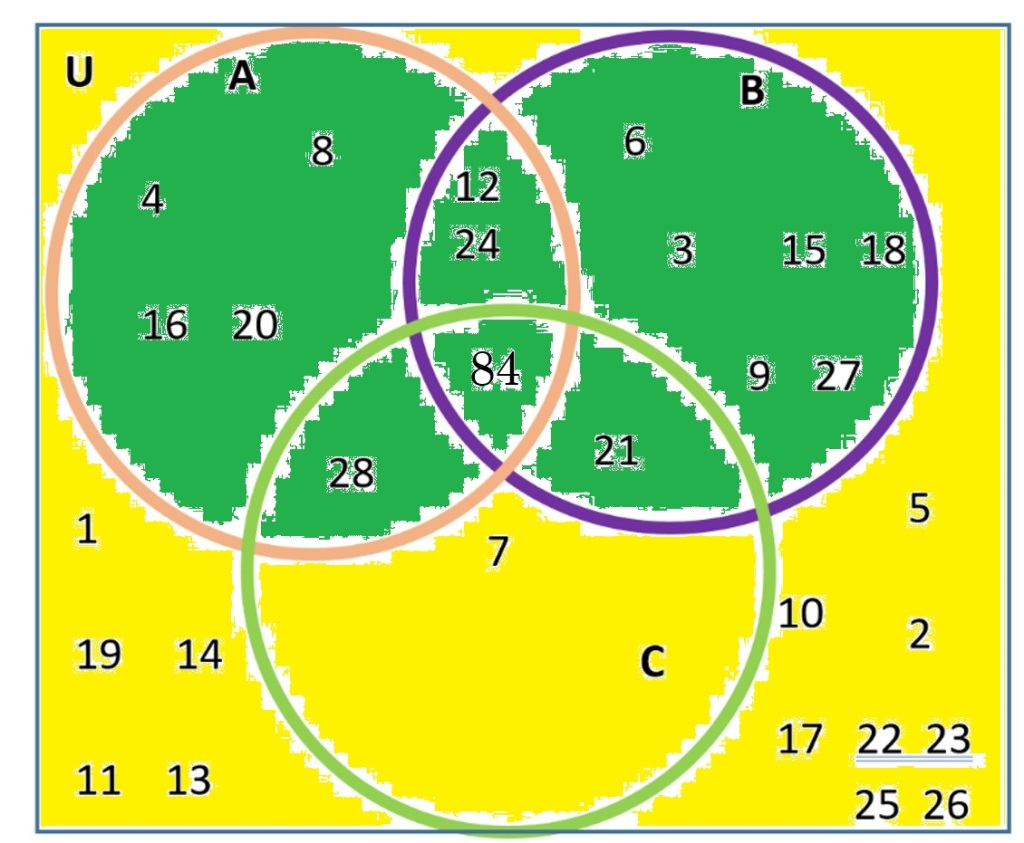
Next, find (A ∪ B)^|, which is everything not colored dark green. This is colored in yellow in the picture. It is regions VII and VIII.

To find (A ∪ B)^| ∪ C, we want to find the union of the last answer,
regions VII and VIII, with set C.

Set C is colored light green; it is regions V, IV, VI, VII.

Careful! Union means to take all. So now to find the union, we must take all of what we colored in yellow, with all of what we colored in light green. That is, regions VII and VIII with regions V, IV, VI, VII.

The answer is all of the colored-in area, in either one color or the other. This gives us regions VII, VIII, V, IV, VI, VII.

(A ∪ B)^| ∪ C = {1, 2, 5, 7, 10, 11, 13, 14, 17, 19, 21, 22, 23, 25, 26, 28, 84}

Union unites everything! Notice that some of A ∪ B is now included, even though it was not before, because it is part of C.

Verbal Method

To find (A ∪ B)^| ∪ C in words, directly translate each symbol:

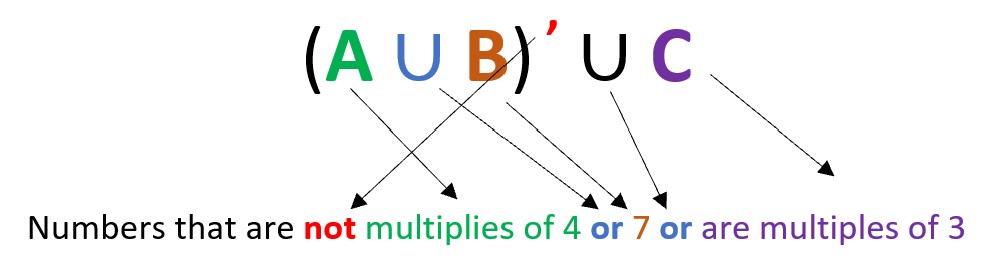
Notice that because (A ∪ B)^| ∪ C has only one ^|, we only use the word not once.

This is a little hard to understand, so we could rewrite the first part of this using DeMorgan’s Laws to see if the translation into words makes more sense.

To use DeMorgan’s Laws, remember that ∪ becomes ∩, and the “not” symbol goes to each element in parenthesis.

We would get (A^| ∩ B^| ) ∪ C. To translate this into words, directly translate each symbol, noting that we now have two nots:

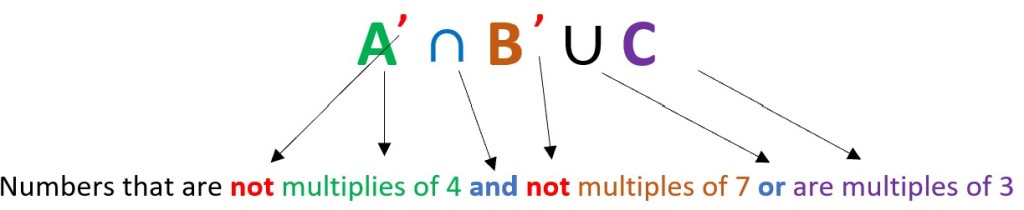
Thus, we have to find numbers that are not multiples of 3 and are not multiples of 4, and unite all of those numbers with the numbers that are multiples of 7.

Check the final list we got using the other two methods: {1, 2, 5, 7, 10, 11, 13, 14, 17, 19, 21, 22, 23, 25, 26, 28, 84} You can see that we have all the numbers that are not multiples of 3 or 4, united with the multiples of 7.

Wait! Why is 21 in there? It’s a multiple of 3! And why is 28 in there? It’s a multiple of 4!

These numbers are in there because they are multiples of 7. Remember, we united everything with the multiples of 7.

You might see that sometimes using DeMorgan’s Laws might not help make the translation easier to understand. In the next example, we look at a set of symbols that is much easier to understand after applying DeMorgan’s Laws.

Example 6: We can also use DeMorgan’s laws to rewrite set expressions that already have “not” in them. Again, this may help the translation make more sense to us.

If we have the following sets, where U = the set of all animals

A = the set of all pets

B = the set of all monkeys

C = the set of all animals that can swim

Using these three sets, how would we translate into words the animals that are in (A^| ∪ B)^| ∩ C? Could we use DeMorgan’s Laws to make the sentence more understandable to see what kind of animals we would have?

(A^| ∪ B)^| ∩ C directly translates to: Not the animals that are not pets or are monkeys, and can swim. The first not is for the complement symbol outside the ( ), and we use a comma to show that part is separate from the next.

Looking at that sentence, I have no idea what kind of animal this could be! Let’s try rewriting the sentence!

First, we “distribute” the not: (A^| ∪ B)^| ∩ C and the union symbol turns upside down. Now we have (A^{| |} ∩ B^|) ∩ C

The A now has two nots! They cancel each other out. A double negative becomes a positive, just like –(–3) = +3

We now have (A ∩ B^|) ∩ C, which translates to: The animals that are pets and not monkeys and can swim. That makes more sense! I can imagine a pet dog that can swim would be in that category. 😊