Chapter 3, Section 4

Math Topics – Writing Sets Using Inequalities, Subsets

Elementary Education – One-to-One Correspondence in Children, counting

When children first start counting, they may know their numbers, but they don’t always use those numbers to judge quantities, looking instead at other characteristics, such as which one is more “spread out” or “taller.” You might remember from chapter 1 that this is because they are in what Piaget called the pre-operational stage of development. But when a child is prompted to count and match, they may begin to use numbers to judge quantities, matching the set they see, to the set of numbers.

The natural numbers

When children count, they are using what we call the set of natural numbers. As with all sets, we can list this set inside braces: {1, 2, 3, 4, …}. Notice the dots on the right indicate that the counting numbers keep going up, past 4. We need to use the dots because it is impossible to list all the natural numbers, since they continue infinitely. We can also use the special symbol, ℕ, to show the set of natural numbers.

Example 1 If we want to write that 3 is an element of the natural numbers, we write: 3 ∈ {1, 2, 3, 4, …}. We can also write 3 ∈ ℕ.

What about 7 and -3, are each of these numbers also an element of the natural numbers? How would you write your answer using set notation? Try to answer this question yourself before scrolling down.

[spoiler space… don’t scroll down until you’ve tried it!]

[don’t scroll down until you’ve tried it….]

Yes, 7 is an element of the natural numbers because the natural numbers keep going up past 4. We write 7 ∈ {1, 2, 3, 4, …}, or 7 ∈ ℕ.

But the negative numbers are not part of the Natural numbers, so we write -3 ∉{1, 2, 3, 4, …} to say that -3 is not an element of the natural numbers, or -3 ∉ ℕ.

The Integers

The integers are both positive and negative whole numbers, and zero. How would you list the integers? Just as with the natural numbers, we would not be able to write them all — but this time, we would need dots in the front and at the end, to indicate that the integers go in both directions: {…,-4, -3, -2, -1, 0, 1, 2, 3, 4, …}. There is also a special letter to indicate the integers, Z (from the German word, Zahlen, meaning numbers). We will not emphasize that in this textbook, but you are welcome to use it if you would like to.

Notice that to list a set without saying the rule, we must give enough of a example that people can figure out the rule — usually at least three numbers. For example, if I want to list the multiples of 2, listing {2, 4, …} would not be enough — someone might say that this was a list of powers of 2, for example. To show multiples of 2, I would write {2, 4, 6, 8, …}; to show powers of 2, I would write {1, 2, 4, 8, 16, …}.

Example 2 write the following in list form, with the dots in the correct places, and at least three numbers:

a. The positive and negative odd numbers

b. The integers less than -3

c. The square numbers

d. The multiples of 5

Try to answer these questions yourself before scrolling down.

[don’t scroll down until you’ve tried it!]

[spoiler space….]

[spoiler space….]

a. {…,-7, -5, -3, -1, 1, 3, 5, 7,…} Note that we have dots at both ends to indicate that the numbers go down lower than -7 at one end, and up higher than 7 at the other. You might have listed one less number at either end, or put some more numbers there, that’s fine.

b. {…-7, -6, -5, -4} The dots are only on the left side, showing that the numbers keep going down (to the left on the number line).

c. {1, 4, 9, 16, 25,…} Note that the square numbers are only positive, because they are gotten from squaring numbers. For example, 16 is gotten when you square 4 or -4.

d. {…,-15, -10, -5, 0, 5, 10, 15,…} The multiples of 5 are both positive and negative, since they are gotten by multiplying any integer by 5. For example, -15 = -3 × 5, -10 = -2 × 5, 5 = -1 × 5, and 0 = 0 × 5, etc. We have dots at both ends to indicate that the numbers go down lower than -15 at one end, and up higher than 15 at the other.

A way to describe sets without having to list the elements is called Set Builder Notation. We can describe the elements by stating the rule in words or by using symbols. We still use curly braces to indicate a set, and we begin with a variable to show that the elements in the set vary according to a rule.

We begin with: {x |

This is read as “the set of all x such that” which is a mathematical way to say that the rule is about to follow.

Then we write the rule in words or symbols, and end with the closing brace }.

Example 3 Using set builder notation, describe the sets using set builder notation:

a. {5, 6, 7, 8…}

b. {….5, 6, 7, 8}

Notice that in a., the numbers start at 5 and keep going up. The dots, …., after the 8 indicate that the numbers keep going up forever after the 8. In b, the numbers go down (lower) on the left side, so we can think of them as starting at 8 and going lower. The “starting” number for the set is on the side that does not have dots. With that information, how would you describe the numbers using words, and then using an inequality symbol like > or < ?

a. In words, we could write {x|x is a natural number greater than or equal to 5}, since the numbers start at 5 and keep going up. In symbols: {x |x > 5 and x ∈ ℕ} We read this as “The set of all x such that x is greater than or equal to 5 and x is an element of the natural numbers.”

Why do we need to include that x is a natural number? Because if we do not, we are describing a set that includes all numbers greater than or equal to 5, including fractions and decimals: {5, 5.1, 5¼,…, 6, 6.9, 6.917, ….}

Note that we could also write or {x |x > 4 and x ∈ ℕ}, “The set of all x such that x is greater than 4 and x is an element of the natural numbers.”

Check your understanding of the symbols and terminology! How would you write {9, 10, 11, ….} in set builder notation? What about {…-3, -2, -1, 0, 1, 2}?
And is this a true statement: 12 ∈ {9, 10, 11, ….}? What about this: 2 ∉ {9, 10, 11, ….}? And finally, is this true: 9.5 ∈ {9, 10, 11, ….}? Why or why not?
Check here after you think about it.

Example 4 Describe the set {3, 4, 5, 6} using set builder notation.

In words, we could write {x|x is a natural number between 3 and 6, including the 3 and the 6}.

Using symbols, we have {x|x > 3 and x < 6 and x ∈ ℕ} or we can write the inequality as one inequality: {x| 3 < x < 6 and x ∈ ℕ}. Note that we place x in the middle, and the inequalities point in the same direction as each other, with 3 less than x, x less than 6, and 3 less than 6. If it is difficult for you to list it all in one expression, that’s okay, just write the two separate inequalities.

Need help? Watch this video where I go over inequalities in more detail!

Example 5 Try describing each of the following sets in words and using symbols:

a. {10, 11, 12}
b. {7, 8, 9, 10….}
c. {1, 2, 3, 4, 5}
d. {…, 3, 4, 5}

Try this yourself before looking at the answers!

Think about each one! The last one is a little tricky.

a. {7, 8, 9, 10….} can be described as {x| x is a natural number greater than or equal to seven} or, using symbols, {x| x > 7 and x ∈ ℕ}

b. {10, 11, 12} can be described as {x| x is a natural number between 10 and 12, inclusive} or, using symbols, {x| 10 < x < 12 and x ∈ ℕ}

c. {1, 2, 3, 4, 5} can be described as {x| x is a natural number less than or equal to five} or, using symbols, {x| x < 5 and x ∈ ℕ}

d. {…., 3, 4, 5} is a bit trickier! Do you think the numbers are meant to go past 1 into the negatives numbers, or do they stop at 1? If they stop at 1, then we can use the same notation as before, {x| x < 5 and x ∈ ℕ}. However, the …. (dots) would usually mean the numbers keep going down, past 1. In that case, we write, {x| x < 5 and x is an Integer}.

How would you write {14, 15, 16, 17} in set builder notation? How is it different from {14, 15, 16, 17, ….}?
Check your answers here.

Subsets

See this video for subsets.

The symbol ⊆ means “is a subset of.”

A is a subset of B if every element of A is contained inside B.

We write A ⊆ B.

Example 6 The set of smile emojis is a subset of the set of silly emojis:

{☺🌝😆} ⊆ {☺🌝😐😆😴😩☹}

It is a subset because all of the smile emojis are inside the set of silly emojis.

But the set of alarm emojis is not a subset of the set of silly emojis:

{‼😩⏰⚠} ⊈{☺🌝😐😆😴😩☹}

We use the ⊈ symbol to mean “is not a subset of.” It is not a subset because all of the alarm emojis are not inside the set of silly emojis. The two sets overlap, but some of the symbols, like ‼⏰⚠ are not in the other set.

Example 7 If I have set A = {4, 5, 6}, set B is {1, 2, 3, 4, 5, 6, 7} and set C is {6, 7, 8, 9}, which of the following is true, A ⊆ B, A ⊆ C or C ⊆ B?

In other words, is {4, 5, 6} ⊆ {1, 2, 3, 4, 5, 6, 7}?

Is {4, 5, 6} ⊆ {6, 7, 8, 9}? Is {6, 7, 8, 9} ⊆ {1, 2, 3, 4, 5, 6, 7}?

Only the first is true, A ⊆ B, because only that one has all of the first set, A inside of the second set, B. The other sets overlap, but one is not entirely inside the other.

If two sets overlap, that is not the same as one being a subset of the other. To be a subset, one set must be entirely inside the other.

Example 8 Is the set of all dogs a subset of the set of all animals, or the other way around? Is the set of all multiples of 2 a subset of the set of all multiples of 4, or is the set of all multiples of 4 a subset of the set of all multiples of 2?

Sometimes it can be hard to figure out which way around a subset goes. One tip is to think which one is a part of the other, or which one is inside the other, and smaller than the other. For the second question, try the problem solving strategy of making a list of each, then think of which list is contained inside the other.

The set of all dogs is a subset of the set of all animals, since all dogs are a type of animal. We can write dogs ⊆ animals.

The set of all multiples of 4 a subset of the set of all multiples of 2 because the set {…4, 8, 12…} is inside {…2, 4, 6, 8, 10, 12…}.

We write {…4, 8, 12…} ⊆ {…2, 4, 6, 8, 10, 12…}.

Check your understanding of the symbols and terminology! Is the set {9, 11} a subset of {9, 10, 11, ….} ?
What about the set {8, 9, 10}, is it a subset of {9, 10, 11, ….} ?
Check your answers here after you think about it.

The empty set and the set itself

Example 9 Is the set of all green dogs a subset of the set of all dogs?

Yes!

There are no green dogs, but just in case there were, they would be inside the set of all dogs. So, this empty set is a subset of the set of all dogs. We would write

Green dogs ⊆ All dogs,

or ∅ ⊆ All dogs

The empty set is a subset of any set.

Is the set of yellow shapes a subset of the set of yellow shapes? Yes!

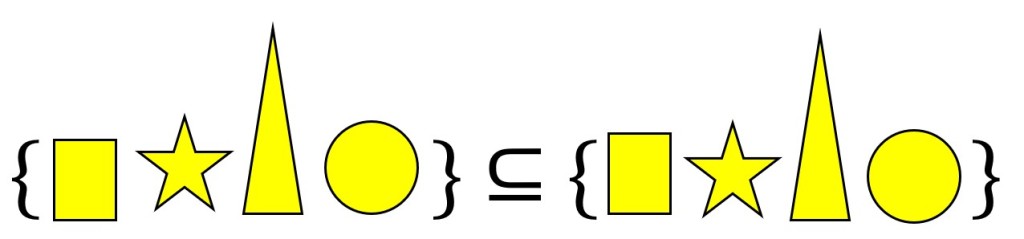
A set is always a subset of itself.

Think of the subset symbol ⊆ as similar to a < symbol, which allows the number to be less than or equal to – for example, 5 < 7 is true, and also 5 < 5 is true.

Finding All the Subsets

How many subsets does this set have?

To figure this out, remember that the empty set and the set itself are always subsets of a set. Thus, ∅ is a subset of the star set, and the star is a subset of itself.

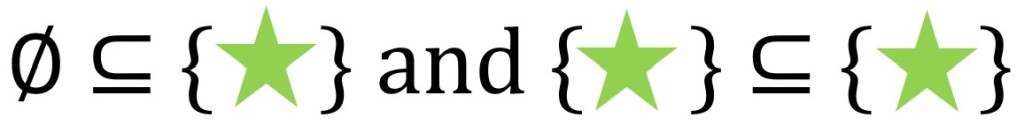
Any one-element set has exactly two subsets – the empty set and the set itself.

What about a two-element set, how many subsets does it have? How many subsets are contained in the set {c,d}?

• We know the empty set is a subset of any set: ∅ ⊆ {c,d}
• The set {c} is a subset of {c,d}.
• The set {d} is a subset of {c,d}.
• The set itself, {c,d} is a subset of {c,d}.

Any two-element set has exactly four subsets.

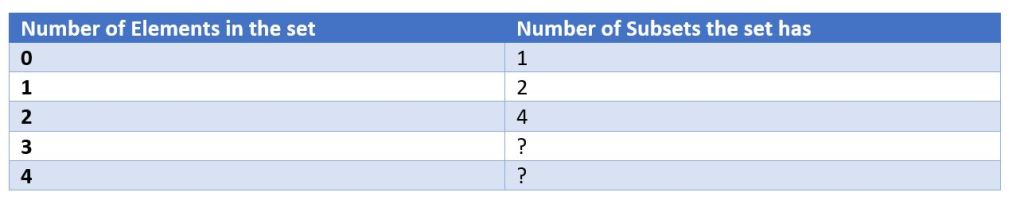
Based on this pattern, how many subsets do you think a three-element set will have? We can use the problem-solving strategy of making a table to see what the pattern is in the number of subsets.

There are many possibilities! Maybe the pattern is 1, 2, 4, 6, 8, adding 2 each time after the first?

Maybe the pattern is 1, 2, 4, 8, 16, multiplying by 2 (doubling) each time?

Maybe we add 1, then add 2, then add 3, like the triangular numbers…..

Remember from playing “Guess my Rule” that having only two or three instances of a rule makes it nearly impossible to figure out the rule! Let’s try it out a three-element set to see if that helps us more.

Here’s a three-element set: {x, y, z} What are its subsets?

• We know the empty set is a subset of any set: ∅ ⊆ {x,y,z}
• The set {x} is a subset.
• The set {y} is a subset.
• The set {z} is a subset. We have just listed all the one-element subsets.
• The set {x, y} is a subset.
• The set {x, z} is a subset.
• The set {y, z} is a subset. These are all the two-element subsets.
• The set itself, {x, y, z} is a subset.

Notice that if I listed {y, z} as a subset, {z, y} is not a separate subset. With sets, the order of the elements does not matter, it does not make a difference. {y, z} is the same set as {z, y}

Any three-element set has exactly eight subsets.

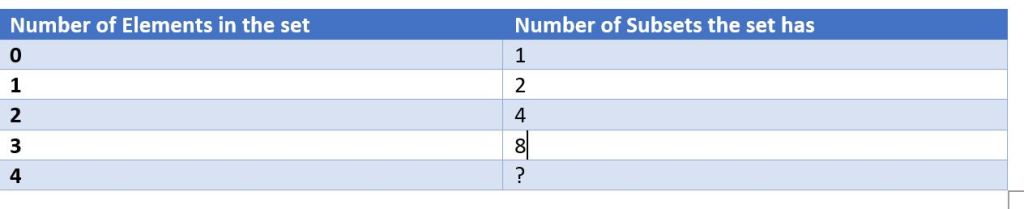
What pattern do you see now? How many subsets do you think a 4-element set will have? Write a formula using n to show the number of subsets.

The number of subsets doubles in each row. A 4-element set will have 16 subsets.

The formula for the number of subsets is 2ⁿ, where n is the number of elements in the set.

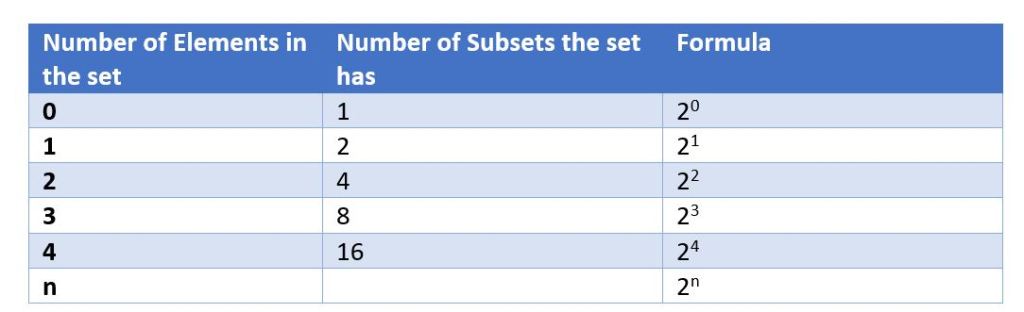
For example, a set with 3 elements has 2ⁿ = 2³ = 8 subsets.

A set with 4 elements has 2ⁿ = 2⁴ = 16 subsets.

Example 10 How many subsets will the set {3, 4, 5, 6, 7, 8} have?

The set {3, 4, 5, 6, 7, 8} has 6 elements in it. Use the formula for subsets, 2ⁿ, with n = 6. We get 2⁶ = 64. The set {3, 4, 5, 6, 7, 8} has 64 subsets!

Check your understanding of the number of subsets of a set! How many subsets does the set {9, 11} have? How do you know? What are the subsets? Write the subsets down, then check here to see if you got them all.