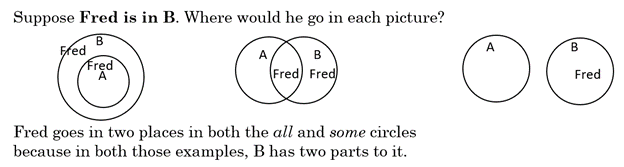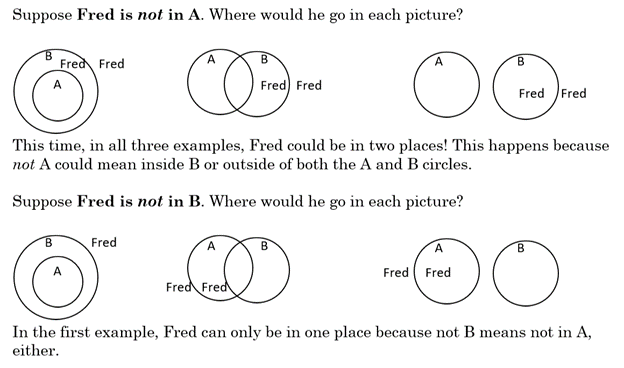Chapter 3, Section 5

Math Topics – Continuing with Subsets; Euler Diagrams: “All”, “Some” and “None”

Elementary Education – Engaging Multiple Learning Modalities

Engaging Multiple Learning Modalities

At all ages and at all ability levels, it’s important to engage students in many different ways – using lecture (for people who learn through listening) and group work (for people who learn through interactions); using all senses and multiple representations (visual and touch and sound). This section shows you how visual representations can help with thinking logically.

Do you notice anything about these buttons?

Look at the big buttons. What can you say about the colors of the big buttons?

What about the little buttons? What colors do we have there?

We might notice that some of the little buttons are white. Another way to say this is: Some of the buttons in the little buttons circle are also in the circle of white buttons. Here, the two circles overlap.

We could also re-sort these buttons to see that the big buttons are all white. Another way to say this is: All of the big buttons are white. The big buttons are inside the circle of all white buttons. This means the set of big buttons, B, are a subset of the set of white buttons, W. As introduced in the previous section, we write B ⊆ W.

In this section, we’ll see that the types of circles you see in these two pictures are called Euler Diagrams.

Euler Diagrams

Euler diagrams are much like Venn diagrams, except that with Euler diagrams, we can put an object in more than one place if we are not sure where it should go. We can use Euler Diagrams to describe relationships about “all,” “some” and “none.”

All relationships A relationship with the word “all” will always be one set inside another set.

All cats are animals.

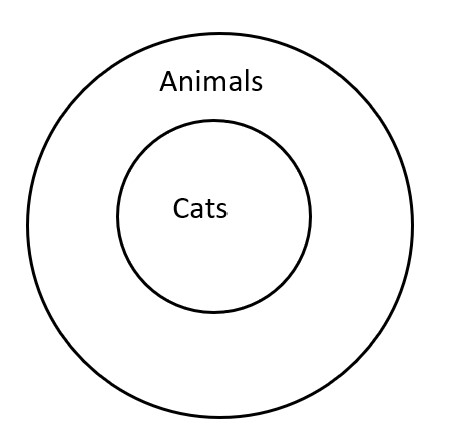
This diagram shows that the entire cats circle is inside the circle for animals. This means that cats is a subset of animals.

Cats ⊆ Animals

Whenever we say an “all” statement, all of the first word in the sentence is inside all of the second word. Think again of subsets, where all of the first set is inside the second set. Cats ⊆ Animals means the set of cats is inside the set of animals.

Example 1 Draw an Euler diagram to show that all birds can fly, and write which set is a subset of the other.

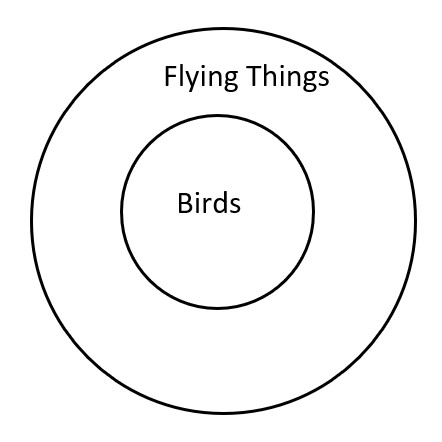
All birds can fly.

Birds ⊆ Flying things

Again, the first item in the sentence, birds, is inside the second one, flying things. Notice that we had to change “can fly” into “flying things,” since Euler Diagrams, like Venn Diagrams, are about objects, or elements.

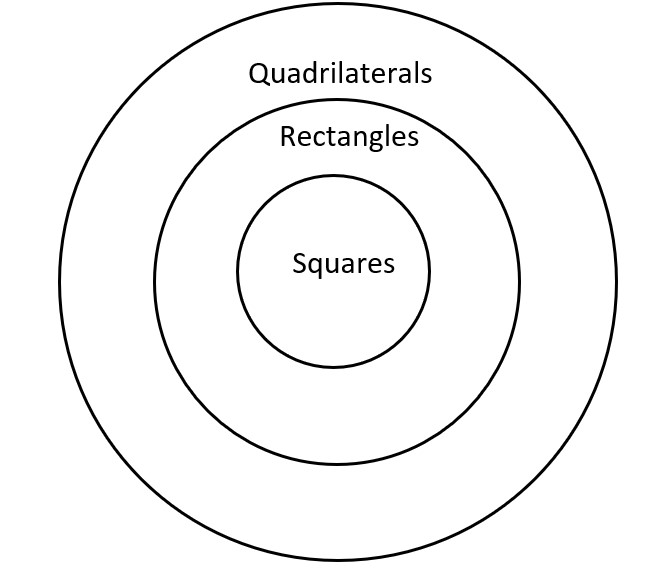
Example 2 Draw an Euler diagram to show that all squares are rectangles and all rectangles are quadrilaterals (have four sides).

For this picture, think of three circles (square shapes, rectangles, and quadrilaterals) all inside each other. Remember that the first object in the sentence goes inside the next one.

All squares are rectangles.

All rectangles are quadrilaterals.

Squares ⊆ Rectangles

and

Rectangles ⊆ Quadrilaterals

Some relationships A relationship with the word “some” will always be one set overlapping another set.

Some cats are pets.

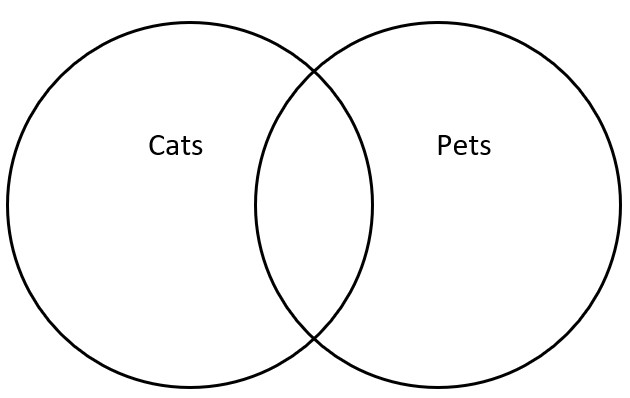
This means that there are some elements in the intersection between cats and pets.

Cats ∩ Pets ≠ ∅

(The intersection between cats and pets is not empty.)

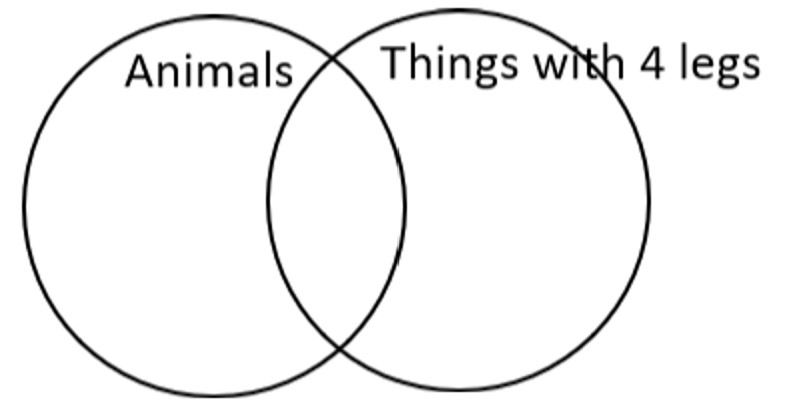
Example 3 How would you use an Euler Diagram to represent “Some animals have four legs?”

Some animals have four legs.

Again, we had to change “have four legs” into a set that could have objects inside it, “things with four legs.”

Animal ∩ Things with 4 legs ≠ ∅ (The intersection of animals and things with four legs is not empty).

No or none relationships

A relationship with the word “no” or “none” will always be one set separate from the other and not overlapping the other set.

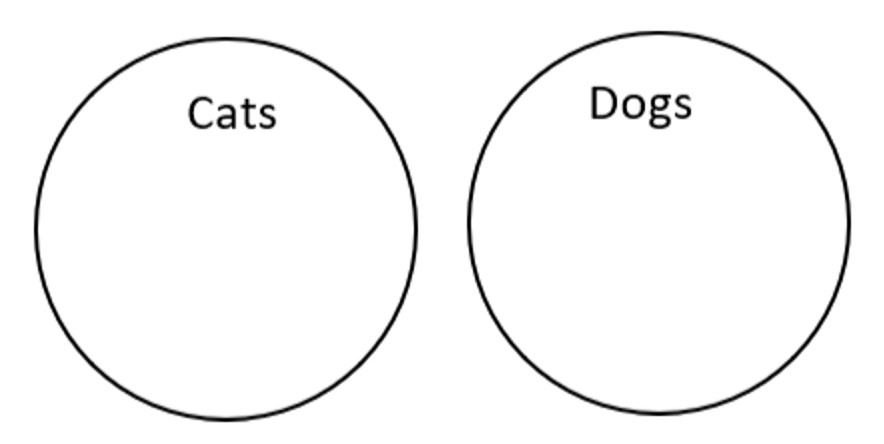
No cats are dogs.

This means that there are no objects in the intersection between cats and dogs.

cats ∩ dogs = ∅

(The intersection between cats and dogs is empty.)

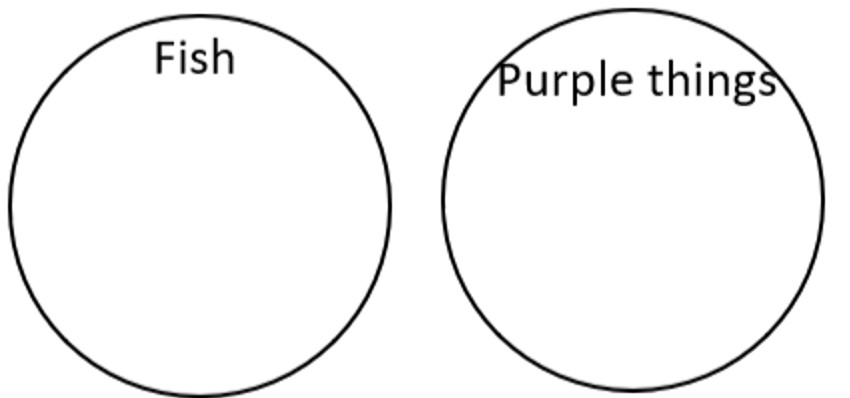
Example 4 How would you use an Euler Diagram to represent “No fish are purple”? Do you think this is a true statement in real life?

No fish are purple means that there are no objects in the intersection between fish and purple things:

Fish ∩ Purple Things = ∅

(The intersection between fish and purple things is empty.)

BUT is this true in real life?

No! There actually are purple fish! The picture below is the purple parrot fish.

In the elementary school classroom, if we are using Euler or Venn diagrams as mental maps, or organizers, we would change our diagram to reflect that we found out this new information, and we would draw:

In logic arguments, though, we pretend that every statement we are given is true. We try not to bring in our own outside knowledge. So, if we are using Euler diagrams to test out whether a logical argument is valid, even though we know there really are purple fish, we pretend the statement “no fish are purple” is true.

Combining all, some and none statements for logical arguments

How would we represent

All cats are furry
and
Some cats are pets

?

How would we represent these statements together in one picture, without bringing in outside knowledge? Is there more than one possible diagram?

We could have either of these pictures:

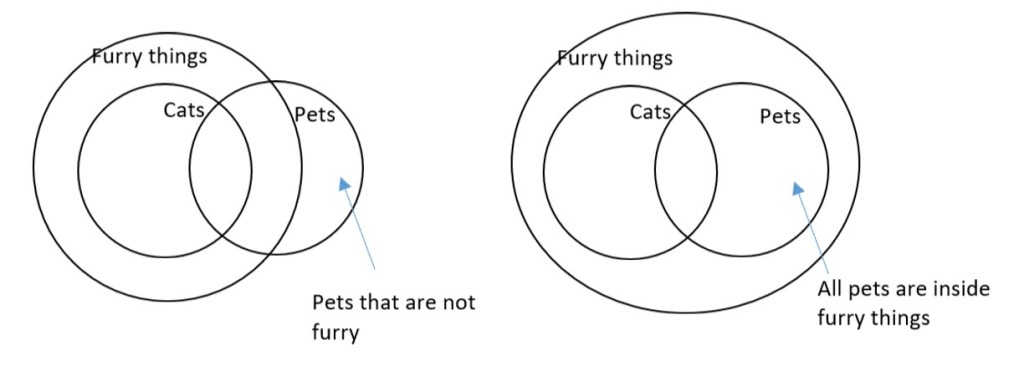
The first picture shows some pets that are not furry. The second picture shows that all pets are furry. Without bringing in outside knowledge, we don’t know which picture is correct so we should draw both of them.

If we are allowed to bring in outside knowledge, we know that there are pets that are not furry (pet fish, for example). But we also know that the statement “all cats are furry” isn’t actually true. The sphynx, for example, is a completely hairless cat.

For this section, please assume that you are taking all statements you are given as true, without bringing in outside knowledge, unless you are explicitly asked to determine a relationship yourself using what you know.

Example 5 Draw one possible correct picture showing these logical statements:

All cats are furry.
All furry things are cute.
Some cute things are birds.

The first statement, “All cats are furry,” means that cats are inside furry things. The second statement, “All furry things are cute,” means furry things are inside cute things.

Next, we need to add in the “some” statement, “Some cute things are birds,” which tells us that birds and cute things must overlap. Without knowing if birds overlap with cute things or maybe they overlap with furry things, we have:

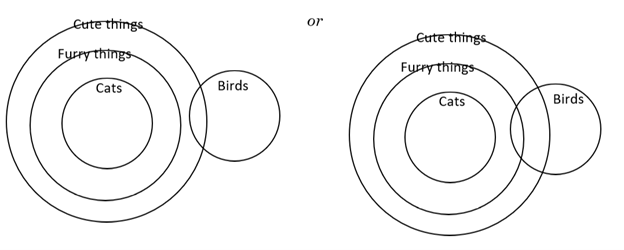
Either of these pictures is correct. Without bringing in outside knowledge, we could even have birds and cats overlapping! Those are the only three possible correct pictures.

Example 6 Sets of Numbers

Finally, let’s look at all the numbers you have studied in this class and in math classes going back to elementary school.

We have the natural or counting numbers denoted by the symbol ℕ. These are the numbers {1, 2, 3, 4, ….}. The natural numbers are all part of the whole numbers, {0,1, 2, 3, 4….}.

ℕ ⊆ Whole Numbers because {1, 2, 3, 4, ….} ⊆ {0,1, 2, 3, 4….}.

The only number that is not in the natural (counting) numbers but that is in the whole numbers, is zero. This is because we don’t usually start with zero when we count, certainly not when we count objects.

Example 7 Where do the square numbers go? The Fibonacci numbers? They are all part of the natural numbers set, so you can think of them as circles inside the natural numbers, or subsets of the natural numbers.

Example 8 Use your knowledge of sets of numbers to determine which statement is correct: “All integers are whole numbers,” or “All whole numbers are integers.” You might want to use the problem-solving strategy of making a list of each type of number to see which type is inside the other.

The set of whole numbers is inside the set of integers, so that means all whole numbers are integers. Whole numbers ⊆ Integers.

In addition, think about where the rational numbers would go. Would the irrationals overlap with the rationals, or not? And where would the natural numbers go?

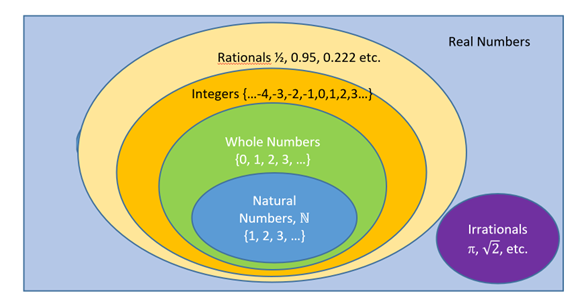
The set of rationals and irrationals do not overlap, since they are the opposites of each other! It is correct to say, no rational numbers are irrational.

It is also correct to say that no integers are irrational, since those two circles also do not overlap.

Placing Elements into Euler Diagrams

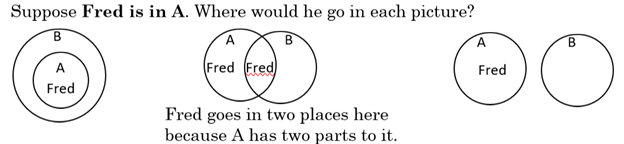
Suppose we know a cat named Fluffy. Where in the circles for “some cats are pets” do we place Fluffy? Note: a whole set is shown using a circle. An object in a set is shown using a letter. We can use F for Fluffy.

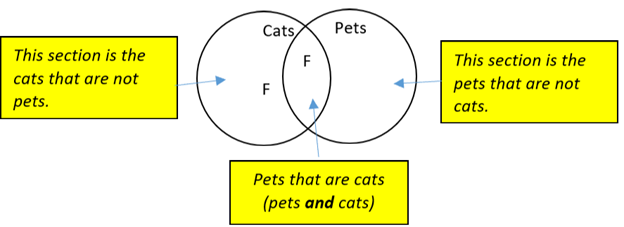
Fluffy is a cat, so must go somewhere in the circle for cats. However, Fluffy could be a cat that is a pet, or might not be a pet. In an Euler Diagram, if we are not sure where an object goes, we put it in all the places it could be. This is in contrast to Venn Diagrams where we know exactly where every object goes, and we always place each object in only one place.

Example 9 Draw a picture showing the logical statements:

All cats are animals.
Fluffy is a cat.
Buster is an animal.

We know Fluffy must go in the cats circle. Fluffy cannot go outside the cats circle, but in the animal circle, because we have been told Fluffy is a cat.

It’s a little more difficult to determine where Buster goes. We know Buster is an animal, so Buster must go in the animals circle, but we don’t know whether Buster is a cat that is an animal. Thus, Buster goes in two places.

Example 10 Draw a picture showing the logical statements:

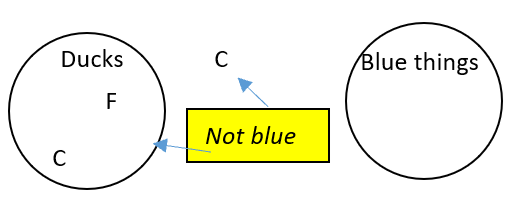
No ducks are blue.
Fred is a duck.
Cindy is not blue.

We know Fred must go in the ducks circle. There is nowhere else Fred can go. Cindy, however, could be in the ducks circle or outside both circles, because all we know for sure is that she is not in the blue circle.

Example 11 Using the diagram of Real Numbers, we can see that zero is a whole number. What other kinds of numbers is it? We see that -1 is an integer. What other kinds of numbers is it? What about pi = 3.14159…., is it anything other than an irrational number?

Since 0 is a whole number, 0 is in the Whole Numbers circle. 0 is also in the Integers circle, since all of the whole numbers are inside of integers. That is, the list of integers includes the whole numbers.

Even though we don’t see zero in the list of rational numbers, it is in the Rationals circle, since all of the whole numbers are inside of the rational numbers. Also, remember from the previous section that rational numbers are numbers that can be written as a ratio of two whole numbers. Since 0 can be written as 0 = 0/1 (or 0/ any number) it is rational.

The number -1 is an integer, and since all integers are also in the Rationals circle, -1 can also go there. Also, -1 can be written as the fraction -1/1.

Pi is also a real number, and so are 0 and -1. (The only kind of number that is not real that you may have encountered is i, the square root of -1, which is imaginary.)

Quick Key (Remember these three diagrams)

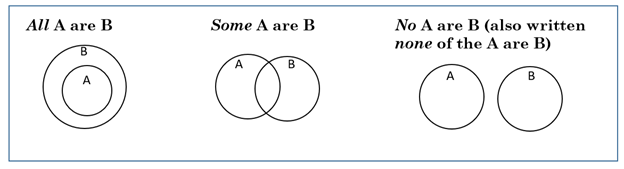
Examples using the Quick Key – where would Fred go in each of the three diagrams?