Sec. 3.6 – Euler Diagrams and Logical Arguments
Chapter 3, Section 6
Math Topics – Euler Diagrams and Logical Arguments, “If…then” (Conditional) Statements
Education Topic – What types of representations are appropriate?
Logical Arguments
In the previous section, we had the example
All cats are animals. Fluffy is a cat.
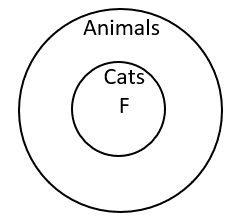
If you look at the diagram (not bringing in your own knowledge), the diagram also shows that Fluffy must be an animal.
We can write this as the conclusion of a logical argument:
| All cats are animals. | Premise 1 |
| Fluffy is a cat. | Premise 2 |
| Therefore, Fluffy is an animal. | Conclusion |
The first two lines of the argument are the premises, the things we take to be true.
The last line is the conclusion.
To be a valid argument, the conclusion must follow from the two premises. That is, if we except that the premises are true, the conclusion must be true based on the premises.
The above argument is valid.
What would make an argument not valid? Let’s try a slightly different set of premises and conclusion:
| All cats are animals. | Premise 1 |
| Dan is an animal. | Premise 2 |
| Therefore, Dan is a cat. | Conclusion |
To check if this is a valid argument, draw a picture only of the premises.
Don’t even look at the conclusion when you are drawing the picture!
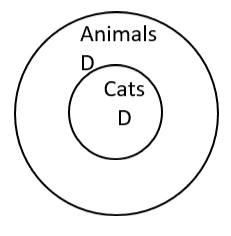
Looking at our picture, we can see that the conclusion, Dan is a cat, is not valid. Dan might be a cat, or Dan might be another kind of animal. The diagram shows that D could be in two possible places.
This means the argument is invalid (not valid).
For an argument to be valid, we must be 100% certain that the conclusion is true based on the premises.
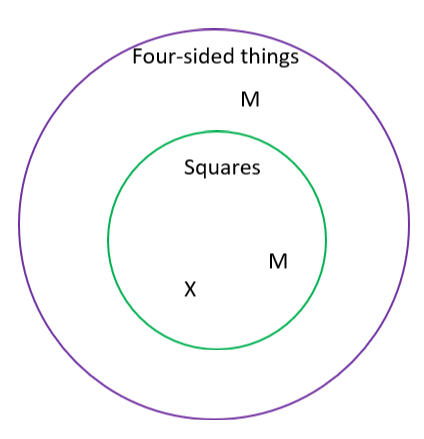
Example 1 Which conclusion is valid?
| All squares are four-sided. | All squares are four-sided. |
| M is four-sided. | X is a square. |
| Therefore, M is a square. | Therefore, X is four-sided. |
To decide, make an Euler diagram using each set of premises, not looking at the conclusion.
The first premise for each is: All squares are four sides. That is pictured with a circle inside a circle. Four-sided things is the outside circle, and squares is inside it. The first part of the all statement is always inside the second part. The second part has more objects in it — there are more four-sided things than just squares. Next, we place M and X in all their correct possible places.
Notice that M can be in two possible places. M must be in the four-sided things circle because that’s the first premise. M could also be in the squares circle because that’s another possible place inside the four-sided things circle.
There is only one possible spot for X, inside the squares circle, since that’s the first premise of that argument. X cannot be outside that circle, since that would mean X was not a square. Remember, we take each of the premises to be absolutely true.
Now we look at the conclusions to see if they follow from the premises.
Is the conclusion, Therefore, M is a square, valid?
No.
Looking at our diagram, we see that M might be a square or might not. M might be outside the squares circle, and just have 4 sides. For example, M might look like this:

M is 4 -sided.
Is the conclusion, Therefore, X is four-sided, valid?
Yes, because X is inside the four-sided things circle. All squares are 4-sided.
When you state your reason why the argument is valid, use only the first part of the reason, above – “Yes, because X is inside the four-sided things circle.” The second part, “All squares are 4-sided,” is just restating the premise.
Restating the premise (even with italics or underlying!) is not enough of a reason to support your argument. Instead, refer to your diagram and explain using the diagram.
Summary
INVALID Argument and reason
All squares are four-sided.
M is four-sided.
Therefore, M is a square.
Invalid because M could be in the part of the circle outside squares (see diagram).
VALID Argument and reason
All squares are four-sided.
X is a square.
Therefore, X is four-sided.
Valid because X must be in the circle of square things, which is inside four-sided things, so this makes X automatically also 4-sided (see diagram).
The Conditional
Another way to show a logical argument is to use symbols instead of, or in addition to, Euler Diagrams.
All cats are animals is the same as saying, If it’s a cat, then it’s an animal.
An “if…then” statement is known as the conditional.
We use an arrow to represent the conditional: c → a, where c is “it is a cat, and a is “it is an animal.” We use three dots, ∴, to represent the word therefore.
Valid argument
| Using “all” | Using the conditional | Symbols |
| All cats are animals. Fluffy is a cat. Therefore, Fluffy is an animal. |
If it is a cat, then it is an animal. It is a cat. Therefore, it is an animal. |
c → a c ∴ a |
Notice that when we use the conditional arrow, we don’t name the cat Fluffy anymore. This is so that the second premise can match the first part of the conditional sentence exactly.
Invalid (not valid) argument
| Using “all” | Using the conditional | Symbols |
| All cats are animals. Dan is an animal. Therefore, Dan is a cat. |
If it is a cat, then it is an animal. It is an animal. Therefore, it is a cat. |
c → a a ∴ c |
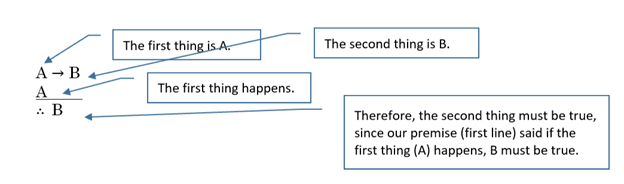
Look carefully at the order of the two arguments, above. Following that pattern, for an if-then statement like A → B, what second line and conclusion will produce a valid argument?
| Valid Argument (Modus Ponens) The order is correct |
Invalid Argument The order is not correct |
| A → B A ∴ B |
A → B B ∴ A |
A valid argument has the second premise and conclusion follow in the same order as they are in the conditional statement.
The official name of the valid argument form is the Latin phrase modus ponens, but it is fine to just say “correct order.”
A student in my class pointed out that the order has to be correct because the conditional arrow is not commutative. What a terrific insight! That is, saying A → B is not the same as saying B → A. Or to go back to our earlier example, if it’s a cat then it’s an animal is not the same as saying if it’s an animal, then it’s a cat.
We can use both an Euler Diagram and symbolic logic to decide if an argument is valid. For some students, the visual representation is easiest; for other students, the symbolic representation is easiest. This is why we want to always try to give our students many ways to represent math!
Example 2 Is the following argument valid or invalid? Use an Euler diagram and symbolic logic with the conditional symbol to decide.
All dogs are friendly.
Bonzo is a dog.
Therefore, Bonzo is friendly.
To decide, first rewrite the argument as a conditional (“If … then”) statement. See which of the above patterns it fits. Finally, check by drawing an Euler Diagram to see visually whether it is valid.
| Using “all” | Using the conditional | Symbols |
| All dogs are friendly. Bonzo is a dog. Therefore, Bonzo is friendly. |
If it is a dog, then it is friendly. It is a dog. Therefore, it is friendly. |
d → f d ∴ f |
This argument is valid because the order of the argument is correct. You have d → f as the first premise, followed by the first letter, d, and the conclusion is the second letter, f. So the second premise and the conclusion go in the same order as the conditional in the first premise.
Or, instead of using the letters d and f, you could think of “dogs” as A and “friendly” as B and you get
A → B
A
∴ B
This is an exact match for the valid argument form, modus ponens, at the top of this page.
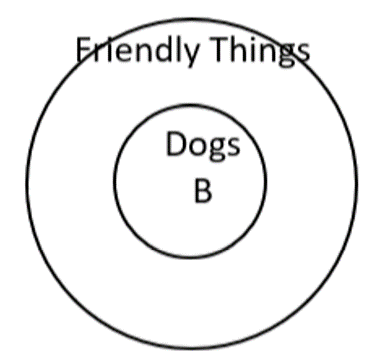
The Euler Diagram brings us to the same conclusion – The argument is valid because Bonzo is inside the “Dogs” circle, which in turn is inside the “friendly things” circle, which means that Bonzo is inside the “friendly things” circle.
Example 3 Is the following argument valid or invalid?
All dogs are friendly.
Rex is friendly.
Therefore, Rex is a dog.
To decide, we rewrite the argument as a conditional to see the pattern. Then we draw an Euler Diagram to see visually whether it is valid.
| Using “all” | Using the conditional | Symbols |
| All dogs are friendly. Rex is friendly. Therefore, Rex is a dog. |
If it is a dog, then it is friendly. It is friendly. Therefore, it is a dog. |
d → f f ∴ d |
This argument is invalid – you can see that the order of d → f, first d then f, is not followed, since the second premise is f, followed by the conclusion of d. If we have d → f, the correct order would have d as the first premise, followed by f. But this argument has f first, followed by d.
Alternatively, you can think of dog as A and friendly as B:
A → B
B
∴ A
This argument is an exact match for the invalid argument form at the top of this page.
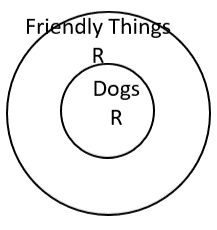
The Euler Diagram brings us to the same conclusion – The argument is invalid because Rex could be in either place. It is not for sure that Rex is inside the “Dogs” circle. To be a valid argument, the conclusion must be 100% sure.
The “not” symbol in logical arguments
In logical arguments, if we want to say “It is not a dog,” we would use the letter d, to mean “it is a dog,” and we would put a not symbol, ~, in front of it: ~d means “not a dog.” This symbol is similar to the complement symbol in sets.
Example 4 Is the following argument valid or invalid?
If it’s green, then it’s not a dog.
It is green.
Therefore, it is not a dog.
To decide, we write the argument in symbols to see the pattern. We also rewrite the statement so we can draw an Euler Diagram to see visually whether it is valid.
| Conditional | Symbols | Words |
| If it is green, then it’s not a dog. It is green. Therefore, it is not a dog. |
g → ~d g ∴ ~d |
No dogs are green Henry is green Therefore, Henry is not a dog. |
This argument is valid: the second premise and conclusion follow in the same order as in the conditional (if … then). That is, in the first line, g → ~d, the g is first and the ~d is second. The next premise, g, and the conclusion, ~d, follow in that same order.
With an Euler diagram, If it’s green, then it’s not a dog would translate into two separate circles. It is the same as no dogs are green.
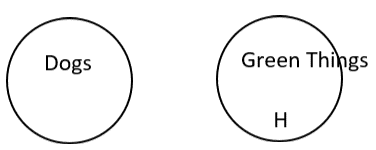
Using the Euler diagram, we can see that the argument is valid since Harry is in the green things circle, so he cannot be in the dog circle, since they don’t overlap.
Logical Arguments using “Some” and “None”
Example 5 Is the following argument valid or invalid?
Some cats are pets.
Fluffy is a cat.
Therefore, Fluffy is a pet.
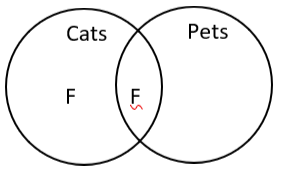
We know from the previous section that we could put F in two places – Fluffy could be a cat that is a pet (in the middle) or a cat that is not a pet (on the left side). Since we do not know for sure that Fluffy is in the cat circle, the argument is invalid. Remember, for an argument to be valid, the conclusion must follow without a doubt from the premises.
In this example, we do not change the argument into symbols, because a some statement does not translate into the conditional.
Some cats are pets is not equivalent to c → p, that would be all cats are pets.
It is important to be able to choose which type of representation – visual or symbolic – is the best one to use for a given situation.
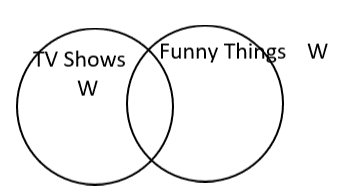
Example 6 Is the following argument valid or invalid? Use an Euler diagram or symbols, whichever is best, to decide.
Some TV shows are funny.
Webster is not funny.
Therefore, Webster is not a TV show.
For any argument with “some”, we cannot use the conditional, so we draw an Euler Diagram. Here we have “Some TV shows are funny.”
Since Webster is not funny, there are two possible places to put Webster that are outside of “Funny Things.” One of these possible places is inside TV shows, so the conclusion, “Webster is not a TV show” is invalid.
All relationships and Transitivity
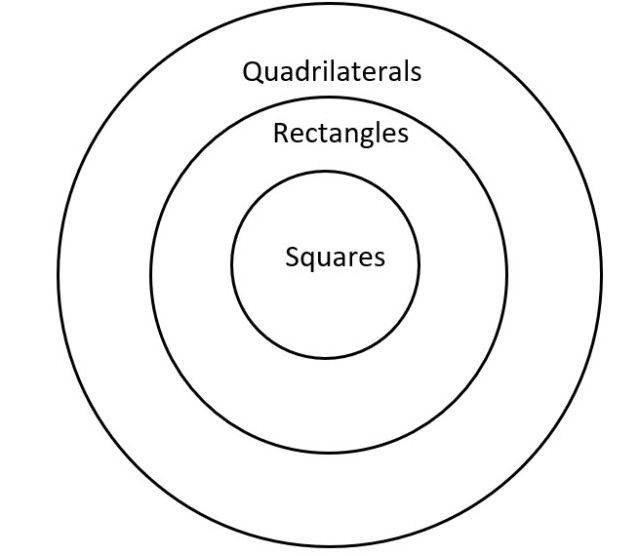
What conclusion is correct to tell us about how squares and quadrilaterals are related?
All squares are rectangles.
All rectangles are quadrilaterals (have four sides).
Therefore, all ____ are _______.
The correct conclusion will create a valid argument.
Use the diagram so see which set will be a subset of the other.
The valid conclusion is Therefore, all squares are quadrilaterals (have four sides).
We know this is true because in our diagram the set of squares is inside the set of quadrilaterals.
We can also use the conditional and symbols to see why.
Conditional Symbols
| If it’s a square then it’s a rectangle. | s → r |
| If it’s a rectangle, then it’s a quadrilateral | r → q |
| Therefore, if it’s a square, it’s a quadrilateral. | ∴ s → q |
The symbols, in order, are s → r, r → q. That is, s → r → q
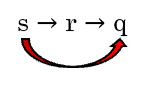
This makes a continuous chain from s, though r, to q. Thus, the conclusion, s → q, is valid.
This type of argument,
A → B
B → C
∴ A → C
is called a valid argument by transitivity.
It shows a chain going from A to B, then B to C, so therefore, A goes to C.
You have probably seen a similar argument, made with inequalities. If one number is less than another, we write a < b. For example, 3 < 4.
Now suppose we know that a < b and we know that b < c. We can write this as one inequality: a < b < c (a is less than b is less than c).
We can conclude that a must be less than c, that is, a < c.
Written with numbers, this is like saying that if 3 < 4 and 4 < 5, we know that 3 < 5.
Just as with the first type of valid argument, the statements must go in order to make a valid argument.
A → B
C → B
∴ A → C
is not a valid argument by transitivity.
It does not show a chain going from A to B, then B to C. Instead, both A and C go to B, so there is nothing linking A to C.
Example 7 Use your knowledge of sets of numbers to create a valid argument by transitivity.
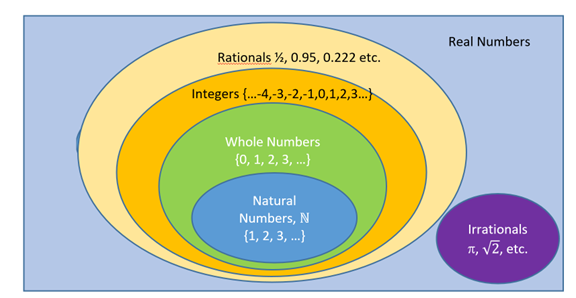
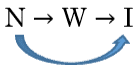
| All natural number are whole numbers. | N→ W |
| All whole numbers are integers | W → I |
| Therefore, all natural numbers are ____? | ∴ N → ? |
You could correctly conclude that N → I. This follows from creating a chain out of the premises: N → W, W → I, means that we have N → W → I
Example 8 Is the following argument valid?
| All whole numbers are integers. | W → I |
| All natural numbers are integers. | N → I |
| Therefore, all whole numbers are natural numbers. | ∴ W → N |
We can see that this argument is invalid by looking at the same diagram – the set of whole numbers is not inside the set of natural numbers,
We can also see that this argument is invalid by looking at the symbols:
W → I, N → I
There is no chain from W to N, each arrow points to I, nothing points to N.
Example 9 Which of the following arguments, shown only with symbols, are valid by transitivity? Which is invalid? Tip: see if you can find a chain leading from one letter in the conclusion to the next.
| Argument 1 | Argument 2 | Argument 3 | Argument 4 |
| p → q | m → z | x → ~y | a → b |
| a → b | m → r | ~y → q | c → b |
| q → r | a → t | q → m | ∴ a → c |
| ∴ p → r | ∴ m → t | ∴ x → q |
Hint: it’s okay to ignore any arguments that are irrelevant — that don’t connect to other arguments.
The first argument can be listed out in one long line, to see what connects to what. We have p → q, a → b, q → r. We can get rid of a → b, since that premise does not have anything in common with the others. Now we have p → q, q → r, which gives us the chain: p → q → r, which means that p does lead to r, p → r. The argument is valid.
Why is it okay to remove an argument in the premises that doesn’t make a difference to your conclusion? Image that the letters stand for statements. Suppose someone said to you, “all pigs are quick” (p → q), all alligators are big (a→ b) and all quick things are rapid (q → r). You could definitely ignore that part about alligators and conclude that all pigs are rapid (p→ r).
For argument 2, we have m → z, m → r, a → t. Since the conclusion has m → t, we are looking for a chain in the premises that links m to t, like this: m → ___ → ___ …→ t. There is no chain that goes from m to t. Instead, we have m going to z and to r, but neither z nor r leads to anything else. The argument is invalid.
For argument 3, we have x → ~ y, ~ y → q, and q → m in the premises. Since the conclusion is x → q, we are looking for a chain in the premises that links x to q. We do have that chain: we have x → ~ y, ~ y → q, which becomes x → ~ y → q, so we have x → q. The argument is valid.
Finally, argument 4 is invalid, since we do not have a chain that goes from a to c in the premises. We have a going to b and we also have c going to b. There is nothing that leads to c. The problem is that the second premise is backwards. If we instead had a → b, and b → c, then we could conclude ∴ a → c.