Sec. 3.7 – The Contrapositive, Combining Argument Types
Chapter 3, Section 7
Math Topics – The Contrapositive, Combining Argument Types
Valid Argument Types
In the previous section, we learned about two valid argument forms that can be made using the conditional (if… then):
| Valid by Modus Ponens | Valid by Transitivity |
| A → B | A → B |
| A | B → C |
| ∴ B | ∴ A → C |
| the order is correct | A chain is made from A to C: A→B, B→C |
We also know that the arguments above can take on many forms. For example,
~B → ~A
~B
∴ ~A
is a valid argument because the correct order is being followed.
That is, ~B is first, followed by ~A in the first premise, then the next statement and conclusion follow in that same order.
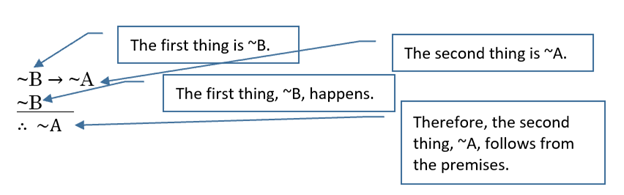
But what if we have the argument
A → B
~B
∴ ~A
This argument does not follow the correct order. But could it still be valid, for a different reason? In this section, we’ll look at a third argument type, to see if the above argument is valid. This third valid argument form is called the contrapositive.
The Contrapositive
The contrapositive is a statement equivalent to A → B, using “not.”
Which one of these, B → A, ~A → ~B, or ~B → ~ A, is the correct equivalent to A → B?
To see, try out the sentence, if’s a cat, then it’s an animal. We’ll call this A→B.
Which sentence means the same thing? That is, if the sentence if’s a cat, then it’s an animal is true, which sentence below is also true?
B → A If it’s an animal, then it’s a cat.
~A → ~B If it’s not a cat, then it’s not an animal.
~B → ~ A If it is not an animal, then it is not a cat.
We are looking for which one of the above sentence is also always true.
[spoiler space…. really think about this.}
[test each sentence out… is it true?]
[can you think of a kind of animal that might make the sentence false?]
The first sentence, If it’s an animal, then it’s a cat, is not true. We can think of other animals, like dogs. So since if it’s an animal, then it’s a cat, is not a true statement, it can’t mean the same thing as our original statement, which was true.
The second sentence, If it’s not a cat, then it’s not an animal, sounds a little better, so let’s try it out. Are there things that are not cats but that are animals? Yes. We can think of things that are not cats, like dogs, that are still animals, so since it’s not true, it can’t mean the same thing.
The last sentence, If it is not an animal, then it is not a cat, is true, and it is the equivalent statement.
The contrapositive of A → B is ~B → ~ A. The two statements are equivalent, which means that if A → B is true then ~B → ~ A must also be true. The contrapositive reverses the direction, and negates each.
Example 1 We know that if a number is a multiple of 4, then it’s a multiple of 2. Think of the number 8, for example. 8 is a multiple of 4 and so also a multiple of 2.
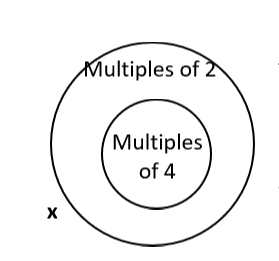
Write the contrapositive and use an Euler Diagram to show that the contrapositive is also true.
If it’s a multiple of 4, then it’s a multiple of 2 is the same as All multiples of 4 are multiples of 2, shown in the diagram.
The contrapositive is if it’s not a multiple of 2 then it’s not a multiple of 4.
To see that the contrapositive is true, look at x, which is not a multiple of 2. Since the multiples of 4 circle is inside multiples of 2, x also cannot be a multiple of 4.
You can also think of a numerical example. Imagine that x = 7. The number 7 is not a multiple of 2, and cannot be a multiple of 4, either.
Notice that if I write the contrapositive incorrectly — for example, if I use the word “not,” but forget to reverse the direction, I get a statement that is not true. For example, If it’s not a multiple of 4, then it’s not a multiple of 2 is not true — think of the number 14, which is not a multiple of 4 but is a multiple of 2.
Or if I reverse the direction but forget the word “not,” I also get a statement that is not true: If it’s a multiple of 2, then it’s a multiple of 4 is not true — again, think of the number 14, which is a multiple of 2, but not of 4.
Looking for examples that show a statement is not true is called looking for a counter example. If you can find an example that contradicts a statement, then the statement is not true — logical statements must be always true.
Example 2 Write the following rule in symbols: If a number is divisible by 6, it must be divisible by 3, then write the contrapositive in symbols and words. What other versions of this statement might seem to be true, but are not?
If a number is divisible by 6, it must be divisible by 3 can be written as 6 → 3.
The contrapositive reverses the direction, and negates each: ~3 → ~6
Thus, the correct equivalent statement is If a number is not divisible by 3, it is not divisible by 6. This statement is true. For example, 20 is not divisible by 3, and not divisible by 6.
Another possible version of this statement, If a number is not divisible by 6, it is not divisible by 3, is not true. For example, the number 21 is not divisible by 6, but it is divisible by 3.
It is also not true that If a number is divisible by 3, it must be divisible by 6. Again, we can use 21, which is divisible by 3, but not by 6.
The contrapositive leads us to a third valid argument form.
We now know that we can replace ~B → ~A with A → B, since they are equivalent statements, by the contrapositive.
This gives us a new valid argument form:
Valid by Contrapositive
A → B This is equivalent to ~B → ~A, so the correct order is still being followed.
~B
∴ ~A
Example 3 Determine whether the following arguments are valid by the contrapositive. Write each argument in symbols and draw an Euler diagram to help you decide.
| If it is a cat, then it’s an animal. | If it’s divisible by 6, then it’s divisible by 3. |
| It is not an animal. | It’s not divisible by 6. |
| Therefore, it is not a cat. | Therefore, it’s not divisible by 3. |
The first argument, in symbols:
c → a
~a each letter in the first premise is negated: ~a
∴ ~ c and the second letter in c → a is negated
and they are in the opposite order from the first premise.
This argument is valid by contrapositive since the order is reversed and each part of the first statement is negated.
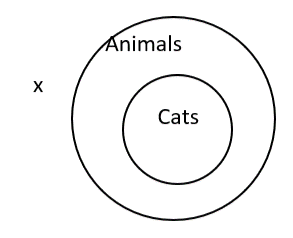
To use an Euler diagram, translate If it is a cat, then it’s an animal, to All cats are animals.
Where we have the second line in the argument, It’s not an animal, think of placing an object, x, that is not an animal, in the right place.
x, would go outside the animals circle. Since that makes it also outside the cats circle, the argument is valid.
The second argument is not valid by contrapositive because even though each part of the statement is negated, the order is not reversed.
6 → 3
~6 each letter is negated (~6, ~3)
∴ ~ 3 but the order is the same.
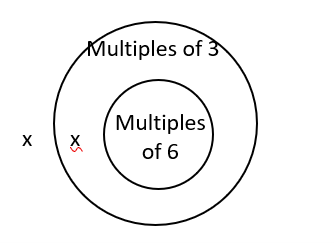
In the Euler diagram for All multiples of 6 are multiples of 3, we see that a number that is not a multiple of 6 could be in two possible places. It might be a multiple of 3. Thus, the conclusion, not a multiple of 3, is not valid, since it is not 100% certain.
Example 4 Use the contrapositive to rewrite the statement, If it’s a fish, then it’s not purple, then create a valid argument. Use both symbols and an Euler diagram to verify that your argument is valid.
The statement can be written f → ~p.
To rewrite f → ~p as the contrapositive, turn the statement around, and negate each part.
We get ~(~p) → ~f, which is the same as p → ~f.
Note that ~(~p) = p, similar to taking the negative of a negative number, which then becomes positive, for example, –( –3) = 3.
So, to create a valid argument from this, we could use the same order as p → ~f. We could have p as the next premise, and ~f as the conclusion.
Our valid argument is now:
| If it’s a fish, then it’s not purple. | f → ~p | Same as p → ~f |
| It’s purple. | p | p |
| Therefore, it’s not a fish. | ∴ ~f | ∴ ~f |
We can also look at the Euler Diagram to see that this makes sense.
If it’s a fish, then it’s not purple is the same as no fish are purple.
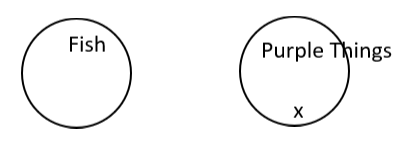
The next line in the argument, It’s purple, means we mark an x in the purple circle.
The conclusion, Therefore, it’s not a fish must be correct, since if x is in the purple circle, it cannot be in the fish circle, since the two circles do not overlap.
Example 5 Which of the following arguments are valid by contrapositive?
|
a. If it’s a dog, then it’s friendly. |
b. If it’s a dog, then it’s friendly. | c. If it’s green, then it’s not a dog. |
| It’s not a dog. | It’s not friendly. | Harry is a dog. |
| Therefore, it’s not friendly. | Therefore, it’s not a dog. |
Therefore, Harry is not green. |
Translate each argument into symbols first, to help you decide.
The symbols would be
| a. | b. | c. |
| d → f | d → f | g → ~d |
| ~d | ~f | d |
| ∴ ~ f | ∴ ~ d |
∴ ~g |
The second and third arguments (b and c) are valid by contrapositive. Argument a is not valid, it is the incorrect application of the contrapositive, because although the two parts of the first premise have been negated, the order was not switched.
Combining Argument Types
We can combine various argument types to get multilayered logical arguments.
Example 6
All natural numbers are whole numbers. N → W
All whole numbers are integers. W → I
All integers are rational numbers. I → R
x is a natural number. N
Therefore, x is a rational number. ∴ R
Remember when we translate into symbols, instead of writing x, we write just N for natural number in one line, and just R for rational in the conclusion.
This is a valid argument. We can tell it is valid by using transitivity: N → W → I → R means that N → R.
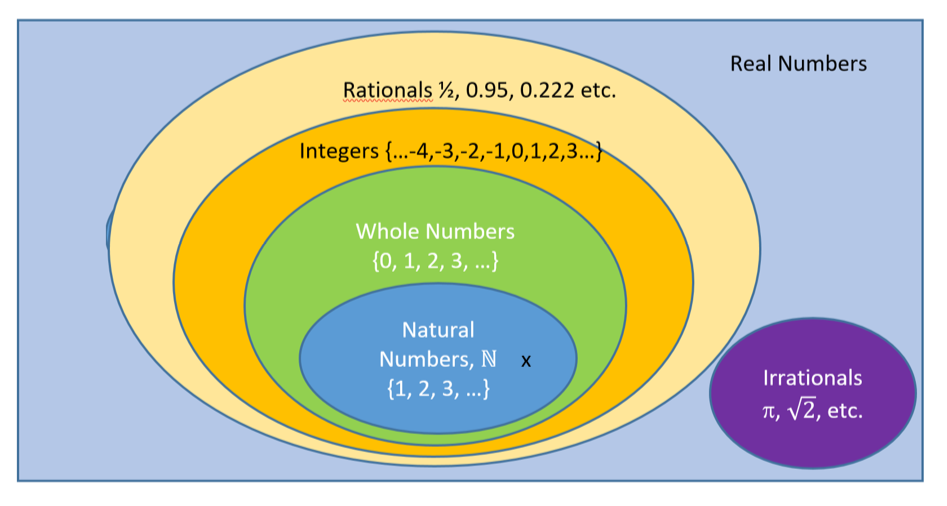
You can also tell from the diagram below. Since x is in N, and N is inside the R circle, x must also be in R.
Using set theory symbols, x ∊ ℕ and ℕ ⊆ R, so x ∊ R.
Example 7 Which of the following arguments, shown only with symbols, correctly combine transitivity and modus ponens (the correct order), or transitivity and the contrapositive? Which are invalid?
| Argument 1 | Argument 2 | Argument 3 |
| p → q | x → ~ y | m → z |
| a → b | ~ y → q | ~m → r |
| q → r | q → m | ~z |
| a | x | ∴ r |
| ∴ r | ∴ m |
Tip: In each argument, look for a “chain” that links the last premise to the conclusion. For example, in argument 1, look for a chain that links a to the conclusion, r.
Argument 1 has a chain that goes from p to r: p → q, q → r, so p → q → r. But there is no chain leading from a to r. We have a → b, but then nothing from b. So argument 1 is invalid, because transitivity is not correctly applied.
In Argument 2, we are looking for a way to link x to the conclusion, m. We have the following: x → ~y, ~y → q, and q → m which gives us x → ~y → q → m. Thus, we have a chain leading from x to m. The argument can be rewritten as
x → ~y → q → m gives us x → m
So we now have
x → m
x ∴ m
Thus, argument 2 is valid, by a combination of transitivity and correct order.
In Argument 3, we are looking for a way to link ~z to the conclusion, r. We don’t see any ~z in the argument, but we can use the contrapositive to turn m → z into ~z → ~m.
| Argument 3 | Is the same as |
| m → z | ~z → ~m |
| ~m → r | |
| ~z | |
| ∴ r | |
We then link this to the next statement: ~z → ~m , ~m → r to get the chain ~z → ~m → r. The argument is valid.
Argument 3 is valid, by a combination of transitivity and contrapositive.