7 Radiometric dating methods

In geology, an absolute age is a quantitative measurement of how old something is, or how long ago it occurred, usually expressed in terms of years.

The earth is billions of years old. The most useful methods for measuring the ages of geologic materials are the radiometric methods-the ones that make use of radioactive parent isotopes and their stable daughter products, as preserved in rocks, minerals, or other geologic materials.

The main condition for the method is that the production rate of isotopes stays the same through ages, i.e. assumes so-called “closed system”. Because of relatively stable sun energy and earth structure we can consider the Earth – Sun system a ” closed system”. The production of isotopes from chemical elements is known as decay rate and it is considered a constant.. Because it is driven by sun activity it was always questioned. Recent article (S. Pommé, et al. Is decay constant? Applied Radiation and Isotopes,Vol. 134, 2018, pp 6-12), see: https://www.sciencedirect.com/science/article/pii/S0969804317303822   explores the decay rate status through experiments.

One of the highlights is: No evidence of variable decay constants due to solar neutrinos.

An isotope is a particular type of atom of a chemical element, which differs from other isotopes of that element in the number of neutrons it has in its nucleus. By definition, all atoms of a given element have the same number of protons. However, they do not all have the same number of neutrons. The different numbers of neutrons possible in the atoms of a given element correspond to the different possible isotopes of that element.

For example, all carbon atoms have 6 protons. Carbon-12 is the isotope of carbon that has 6 neutrons. Carbon-13 is the isotope of carbon that has 7 neutrons. Carbon-14 has 8 neutrons in its nucleus, along with its 6 protons, which is not a stable combination. That is why carbon-14 is a radioactive isotope-it contains a combination of protons and neutrons in its nucleus that is not stable enough to hold together indefinitely. Eventually, it will undergo a spontaneous nuclear reaction and turn into a stable daughter product – a different isotope, which is not radioactive.

Each type of radioactive isotope has a half-life, a length of time that it will take for half of the atoms in a sample of that isotope to decay into the stable daughter product. Physicists have measured the half-lives of most radioactive isotopes to a high level of precision.

Parent Isotopes, Daughter Isotopes, and Half-Lives

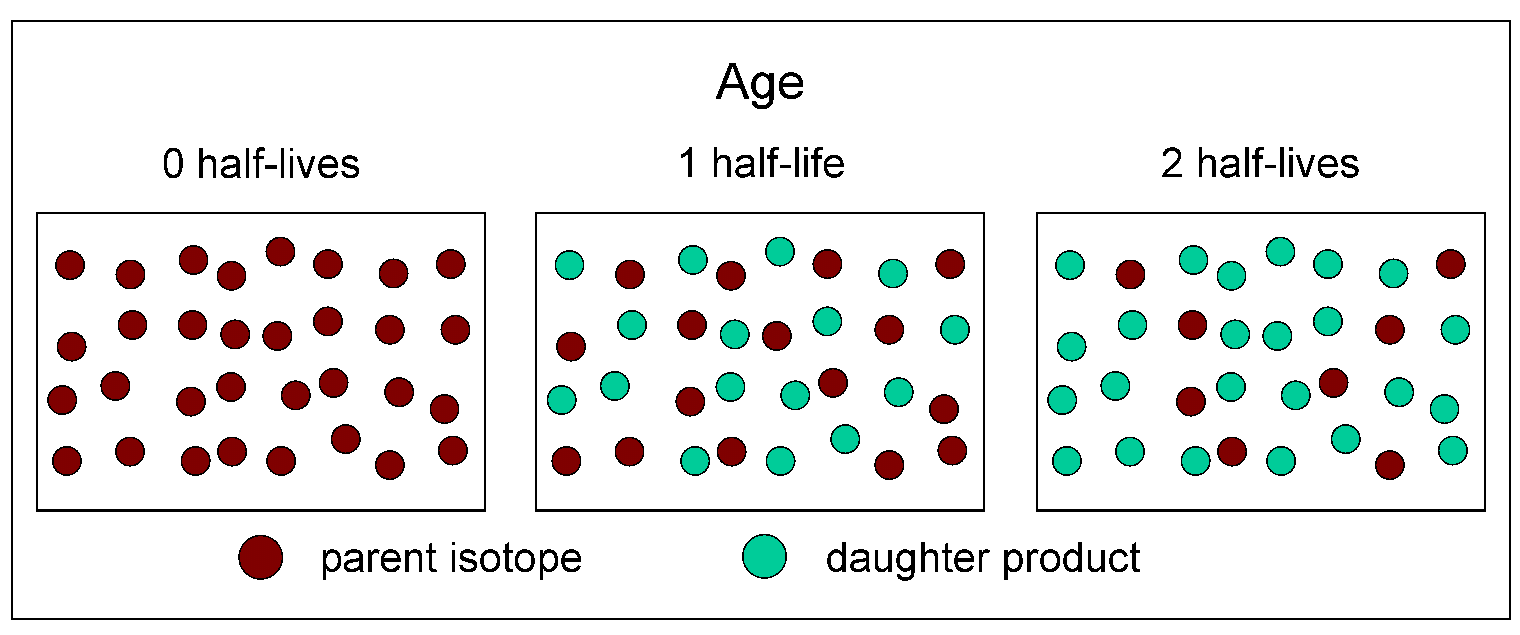
The dots in the cartoon below represent atoms of a parent isotope decaying to its stable daughter product through two half-lives. At time zero in the diagram, which could represent the crystallization of minerals in a rock, there are 32 red dots. After one half-life has passed, there are 16 red dots and 16 green dots. After two half-lives have passed, there are 8 red dots and 24 green dots.

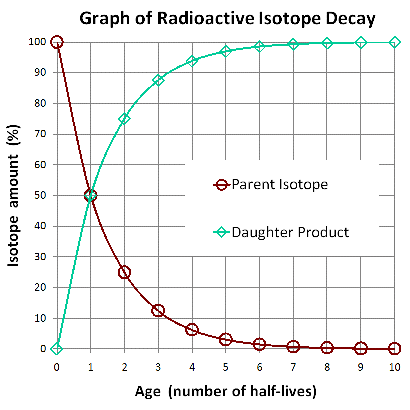
The following graph illustrates radioactive decay of a fixed amount of an isotope. You can see how the proportions of the isotopes from the cartoon above are graphed as percentages at half-lives 0, 1, and 2 below.

The properties of radioactive isotopes and the way they turn into their stable daughter products are not affected by variations in temperature, pressure, or chemistry. Therefore the half-lives and other properties of isotopes are unaffected by the changing conditions that a rock is subjected to as it moves through the rock cycle. If a granite crystallizes with minerals containing radioactive isotopes, it is as though the rock crystallizes with a built-in batch of stopwatches that begin ticking away as soon as the granite has cooled.

Classic examples of key radiometric measurments are:

Development of C14 method by Dr. Libby in 1949, see: https://en.wikipedia.org/wiki/Willard_Libby

Measurement of the age of the Earth (1956) by Dr. Patterson, see: https://en.wikipedia.org/wiki/Clair_Cameron_Patterson

Radiometric age determination

Radiometric age determinations are expensive and time-consuming. A geologist has to be sure that an age of a rock will help answer an important research question before he or she devotes time and money to making a radiometric age measurement.

Before determining the age of the granite, it must be analyzed under a powerful microscope, and with an electron microprobe, to make sure that its original minerals have not been cracked and altered by metamorphism since the rock first formed. Separating the minerals from the granite is the next step in determining its age. High-precision laboratory analyses are then used to measure the amounts of radioactive parent isotope and stable daughter product in the minerals. Once these quantities have been measured, the half-life of the radioactive isotope is used to calculate absolute age of the granite.

Example Problem on Age Calculation:

Uranium (parent) is eventually converted to Lead (daughter). A granite contains crystals with 150 ppma (parts per million by atomic proportions) of Uranium U235 and 1050 ppma of Lead Pb207. The half live decay of U235 to Pb207 is 700 million years. How old is the rock?

Solution:

1. Add parents and daughters: 150 + 1050 = 1200

This is the original number of parents present at the time of the chemical reaction that formed minerals in the rock.

2. We know that the half-life of Uranium is 700 million years (i.e. Uranium parents will decay by half in 700 million years). Keep dividing the total number of parents present at the time of mineral formation by half until we get the number found today (i.e. 150 ppma):

1200 / 2 = 600;            600/2 = 300;                300/2 = 150

3. It took us three divisions to get the present level of U235. Thus three half-lives have passed since the rock formed;

Answer:           3 half-lives x 700 million years = 2100 million years or 2.1 billion years

————————————————————————————————————————————-

The following table lists a selection of isotope pairs that are used in making radiometric age determination. Note that carbon-14 has a relatively short half-life, which makes it useful only for young, carbon-rich geologic materials, less than about 70,000 years old. Igneous rocks and high-grade metamorphic rocks are the most likely to be entirely formed of minerals that crystallized when the rocks formed. As most fossils are found in clastic sedimentary rocks, which are made of weathered and eroded minerals and bits of rock of various ages, it is unlikely to be able to make an radiometric age determination of a rock in which a fossil is found. The age of a rock containing fossils can usually be narrowed down by measuring the ages of metamorphic or igneous rocks in stratigraphic relation to it, such as a lava flow on top of a layer of sedimentary rock.