Distribution of Differences in Sample Proportions (2 of 5)

Introduction

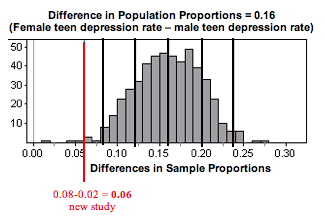
Recall that we are in the middle of an investigation about the difference in female and male teen depression rates. In our investigation, we are assuming that 26% of female teens and 10% of male teens are depressed. That is, we assume a 16% = 0.16 difference favoring girls.

• We saw a 0.06 gender difference in teen depression rates from the National Survey of Adolescents. Again, girls had a higher rate of depression. Does this study suggest that our assumption about a 0.16 difference in the populations is wrong?
• Or could the results have come from populations with a 0.16 difference in depression rates?

At this point, we may have a sense of the answers to these questions for samples of 64 females and 100 males. But we need to look at the long-run behavior of the differences in sample proportions. We also need to investigate the effect of sample size on our conclusion. The samples in the National Survey of Adolescents are very large.

So we continue this investigation in a Simulation WalkThrough.

On the next page, we use the simulation shown in the WalkThrough to make inferences about a difference in population proportions. As we did in Linking Probability to Statistical Inference, we use a simulation to make observations about the sampling distribution before we develop the mathematical model that we will use in inference. The logic we use to make inferences with simulated sampling distributions is the same logic we use with mathematical models. Let’s practice that way of thinking now.

Try It

Suppose in a study of 540 female and 475 male U.S. teens, we find that 8% of the females and 2% of the males are depressed. What does this study suggest about our assumption that the depression rate of female teens is 16% higher than that of male teens in the United States?

Here is a simulated distribution of differences for a large number of independent random samples for these sample sizes. Note that we have rescaled the axis, so the distribution may look wider than the distributions in the WalkThrough, but it actually has less variability.