Module 9: Inference for Two Proportions
Distribution of Differences in Sample Proportions (3 of 5)
Distribution of Differences in Sample Proportions (3 of 5)
Learning outcomes
- Draw conclusions about a difference in population proportions from a simulation.
Now we continue with more examples of using a simulation to make inferences about differences in population proportions.
Example
Abecedarian Early Intervention Project
Recall the Abecedarian Early Intervention Project. In this experiment, researchers selected high-risk infants on the basis of the mothers’ education, family income, and other factors. They randomly assigned some infants to receive 5 years of high-quality preschool. The remaining infants were a control group. All children received nutritional supplements, social services, and health care to control the effects of these confounding factors on the outcomes of the experiment. By age 21, a much larger percentage of the treatment group than the control group had enrolled in college.
Assumption about parameters:
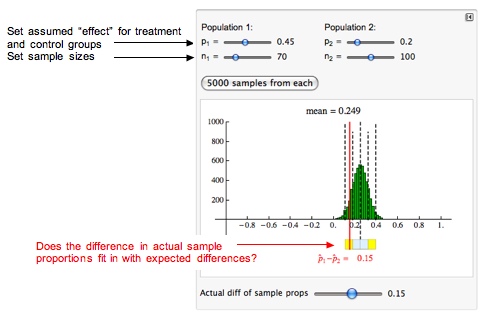
For this example, we assume that 45% of infants with a treatment similar to the Abecedarian project will enroll in college compared to 20% in the control group. We assume that a high-quality preschool experience will produce a 25% increase in college enrollment. We call this the treatment effect.
Let’s suppose that childcare institutions across the United States want to replicate the Abecedarian project. How much variation in results can we expect from fluctuation in random assignment to treatment groups? We know from our previous work that our answer depends on the number of infants we assign to each group.
Actual sample results:
Let’s suppose a daycare center replicates the Abecedarian project with 70 infants in the treatment group and 100 in the control group. After 21 years, the daycare center finds a 15% increase in college enrollment for the treatment group. This is still an impressive difference, but it is 10% less than the effect they had hoped to see. What can the daycare center conclude about the assumption that the Abecedarian treatment produces a 25% increase?
Here we use the simulation from the WalkThrough to do a simulation.
Analysis:
- We assume that the treatment effect is a 25% increase in college enrollment. So we see that the mean of the differences in sample proportions is 0.25. In other words, the differences in sample proportions average out to the difference between the population proportions.
- Typical differences from random assignment appear to fall between about 0.10 and 0.40. This is 2 standard errors from the mean.
- The daycare center achieved a 15% increase. This difference in sample proportions of 0.15 is less than 2 standard errors from the mean, so this result is not surprising if the treatment effect is really 25%.
Conclusion:
Chance variation that comes from random assignment explains the results from this daycare center. The results are not statistically significant. We can view this study as weak evidence that the treatment effect is less than 25%. So this study does not give us evidence strong enough to reject the claim that the Abecedarian treatment produces a 25% treatment effect.
Try It
Example
HPV Vaccine
During a debate between Republican presidential candidates in 2011, Michele Bachmann criticized an executive order made by her opponent, Texas Governor Rick Perry. The executive order required that all sixth-grade girls receive an HPV vaccine. HPV (human papillomavirus) infections are widespread. Some forms of HPV cause cancer. In 2007, the New England Journal of Medicine published the results of two large, randomized, placebo-controlled trials of a vaccine for HPV-related cancer. For the group of girls and women who received the vaccine, the HPV-related cancer rate was much lower than for those who received a placebo.
After the debate, a Congressional Connection Poll asked 1,000 people the following question: “As you may have heard, a few years ago the state of Texas required girls entering sixth grade to receive vaccinations against a virus that can cause cervical cancer in women. These injections were required for all girls unless their parent or legal guardian requested that they not receive them. Do you think Texas was right or wrong to require the vaccinations?” Fifty-seven percent of those polled answered that the state was wrong.
Let’s suppose 55% of all U.S. adults oppose mandatory vaccination against HPV. Let’s also suppose there is no difference between men and women on this issue. So we assume that 55% of all U.S. men and 55% of all U.S. women oppose mandatory vaccination against HPV.
Suppose we ask this same question to a random sample of 100 U.S. men and 150 U.S. women. How much of a difference in poll results will convince us that there are gender differences with this issue?
Use the simulation to do a simulation to answer this question. Enter your answer in the Try It activity that follows.
Click here to open this simulation in its own window.
Try It
Try It
- Concepts in Statistics. Provided by: Open Learning Initiative. Located at: http://oli.cmu.edu. License: CC BY: Attribution
