Estimate the Difference between Population Proportions (2 of 3)

Confidence Interval for a Difference in Two Population Proportions: Beyond the Basics

For all confidence intervals, the margin of error is based on the standard error. We know from “Distributions of Differences in Sample Proportions” that the standard error for the sampling distribution of differences in sample proportions is:

[latex]\sqrt{\frac{p_{1}(1-p_{1})}{n_{1}}+\frac{p_{2}(1-p_{2})}{n_{2}}}[/latex]

Obviously, if we are trying to estimate the difference in population proportions, we will not know [latex]p_{1}[/latex] or [latex]p_{2}[/latex]. So we estimate these population proportions with our sample proportions. This is the same approach we used when had to estimate the standard error for the distribution of sample proportions in Inference for One Proportion. The estimated standard error becomes

[latex]\sqrt{\frac{\hat{p}_{1}(1-\hat{p}_{1})}{n_{1}}+\frac{\hat{p}_{2}(1-\hat{p}_{2})}{n_{2}}}[/latex]

This formula estimates the average error between a difference in sample proportions and the true difference in population proportions.

So a 95% confidence interval has the following formula:

(differenceinsampleproportions) ± 2(standarderror)

[latex]\hat{p_{1}}-\hat{p_{2}}\pm 2\sqrt{\frac{\hat{p}_{1}(1-\hat{p}_{1})}{n_{1}}+\frac{\hat{p}_{2}(1-\hat{p}_{2})}{n_{2}}}[/latex]

We can use this formula only if a normal model is a good fit for the sampling distribution. Recall that this is true only if the expected number of successes and failures in each sample is at least 10. For those who like formulas, these conditions translate into the following inequalities.

n₁p₁ ≥ 10 n₁ (1-p₁) ≥ 10 n₂p₂ ≥ 10 n₂(1-p₂) ≥ 10

We have to adjust these conditions because we do not know the population proportions p₁ and p₂. We make the same adjustment we made in Inference for One Proportion. We require that the actual number of successes and failures in each sample is at least 10. For those who like formulas, these conditions translate into replacing p₁ and p₂ with the corresponding sample proportions. Luckily, this tweak works and the normal distribution still gives fairly accurate confidence levels for different critical z-scores.

Other Levels of Confidence

In Inference for One Proportion, we saw that we can create confidence intervals for other levels of confidence. Changing the level of confidence changes the critical z-score. The following image shows the three most commonly used confidence levels and their critical z-scores.

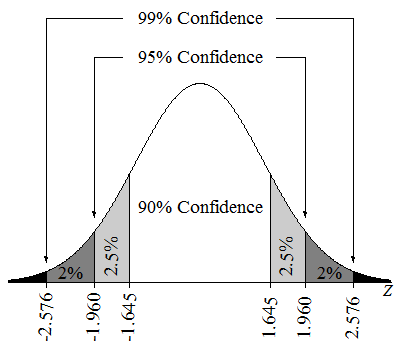
The following table summarizes the critical values for the most commonly used confidence levels.

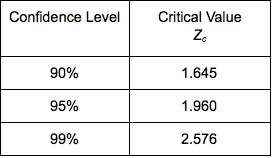
Note: A more exact value for the margin of error of a 95% confidence interval uses Z_c = 1.96 instead of 2 standard errors.