Module 2: Summarizing Data Graphically and Numerically
Interquartile Range and Boxplots (1 of 3)
Interquartile Range and Boxplots (1 of 3)
Learning OUTCOMES
- Use a five-number summary and a boxplot to describe a distribution.
Introduction
Recall that when we describe the distribution of a quantitative variable, we describe the overall pattern (shape, center, and spread) in the data and deviations from the pattern (outliers). In “Distributions for Quantitative Data” and “Measures of Center,” we focused on describing the shape and center of a distribution. We also investigated how the shape influences our choice of measurements of center. In “Quantifying Variability Relative to the Median” and Quantifying Variability Relative to the Mean,” we focus on describing the spread of a distribution more precisely.
We begin with describing spread about the median.
Example
Two Sets of Exam Scores
Consider the following two distributions of exam scores:
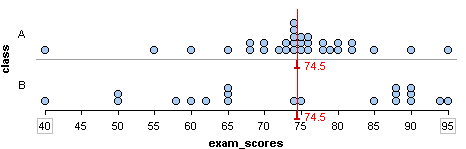
Both distributions have a median of 74.5. Which distribution has more variability?
The answer to this question depends on how we measure variability. Both distributions have the same range. The range is the distance spanned by the data. We calculate the range by subtracting the minimum value from the maximum value.
- Range = Maximum value – minimum value
For both of these data sets, the range is 55 (here is how we calculated the range: 95 – 40 = 55). If we use the range to measure variability, we say the distributions have the same amount of variability.
But the variability in the distributions differ when we look at how the data is distributed about the median. Set A has a large portion of its data close to the median. This is not true for Set B. From this viewpoint, Set A has less variability about the median.
Now we develop a way to measure the variability about the median. To do so, we use quartiles. Quartile marks divide the data set into four groups with equal counts.
Example
Quartiles and the Interquartile Range
We added dividers to show the quartile marks for the two sets of exam scores. Quartile marks divide the data set into four subgroups with the same number of individuals in each subgroup.
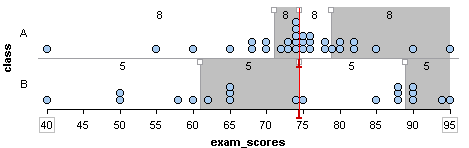
Notice: For a data set, there is an equal amount of data in each quartile.
- Class A has 32 scores, so each quartile contains eight scores (32 ÷ 4 = 8).
- Class B has 20 scores, so each quartile contains five scores (20 ÷ 4 = 5).
The quartiles together with the minimum and maximum scores give the five-number summary:
- Class A: Min: 40 Q1: 71 Q2: 74.5 Q3: 78.5 Max: 95
- Class B: Min: 40 Q1: 61 Q2: 74.5 Q3: 89 Max: 95
Notice: The second quartile mark (Q2) is the median.
Notice: Some quartiles exhibit more variability in the data even though each quartile contains the same amount of data.
- For example, 25% of the scores in Class A are between 40 and 71. There is a lot of variability in this first quartile (Q1). The eight scores in Q1 vary by 30 points.
- Compare this to the third quartile (Q3) for Class A: 25% of the scores in Class A are between 74.5 and 78.5. There is not much variability in Q3. The 8 scores in Q3 vary by only 4 points.
How are quartiles used to measure variability about the median? The interquartile range (IQR) is the distance between the first and third quartile marks. The IQR is a measurement of the variability about the median. More specifically, the IQR tells us the range of the middle half of the data.
Here is the IQR for these two distributions:
- Class A: IQR = Q3 – Q1 = 78.5 – 71 = 7.5
- Class B: IQR = Q3 – Q1 = 89 – 61 = 28
As we observed earlier, Class A has less variability about its median. Its IQR is much smaller. The middle 50% of exam scores for Class A vary by only 7.5 points. The middle 50% of exam scores for Class B vary by 28 points.
Try It
Using the IQR to Identify Outliers
We consider a point an outlier when it is substantially above Q3 or substantially below Q1. To make this statement more precise, we mark off a distance of 1.5 IQRs above Q3 and below Q1. Any point outside of this range is considered an outlier.
We can write this idea as a formula:
A value is an outlier when
- the value is greater than Q3 + 1.5 * IQR or
- the value is less than Q1 – 1.5 * IQR
To make more sense of this rule, let’s look at a visual example.
Example
Using IQR to Identify Outliers
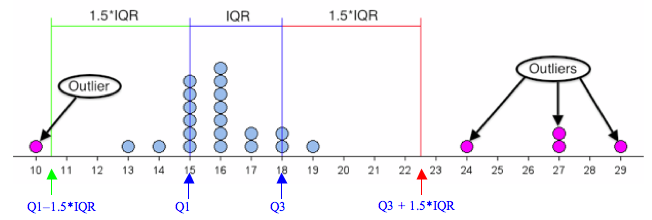
For the data set in the dotplot, Q1 = 15 and Q3 = 18, so the IQR = 18 – 15 = 3.
- Q1 – 1.5 * IQR = 15 – 1.5 * 3 = 15 – 4.5 = 10.5
- This cutoff is shown in green on the dotplot.
- The data point at 10 is considered an outlier because it is below 10.5.
- Q3 + 1.5 * IQR = 18 + 1.5 * 3 = 18 + 4.5 = 22.5
- This cutoff is shown in red on the dotplot.
- The data points at 24, 27, and 29 are considered outliers because they are above 22.5.
The points in purple are outliers by the IQR definition.
Try It
Let’s Summarize
- The range measures the variability of a distribution by looking at the interval covered by all the data. The IQR measures the variability of a distribution by giving us the interval covered by the middle 50% of the data.
- The five-number summary of a distribution consists of the minimum, quartile 1, median, quartile 3, and maximum.
- The IQR is the measure of spread we should use when using the median to measure center.
- When using the median and IQR to measure center and spread, a data point is considered an outlier if it satisfies one of the following conditions.
- The data value is more than 1.5 IQRs greater than Q3 (i.e., the value is greater than Q3 + 1.5 * IQR)
- The data value is more than 1.5 IQRs less than Q1 (i.e., the value is less than Q1 − 1.5 * IQR)
- Concepts in Statistics. Provided by: Open Learning Initiative. Located at: http://oli.cmu.edu. License: CC BY: Attribution
