Module 7: Linking Probability to Statistical Inference
Statistical Inference (1 of 3)
Statistical Inference (1 of 3)
Learning OUTCOMES
- Find a confidence interval to estimate a population proportion when conditions are met. Interpret the confidence interval in context.
From the Big Picture of Statistics, we know that our goal in statistical inference is to infer from the sample data some conclusion about the wider population the sample represents. In the first section, “Distribution of Sample Proportions,” we investigated the obvious fact that random samples vary. Because different samples may lead to different conclusions, we cannot be certain that our conclusions are correct. Statistical inference uses the language of probability to say how trustworthy our conclusions are.
We learn two types of inference: confidence intervals and hypothesis tests. We construct a confidence interval when our goal is to estimate a population parameter (or a difference between population parameters). We conduct a hypothesis test when our goal is to test a claim about a population parameter (or a difference between population parameters). Both types of inference are based on the sampling distribution of sample statistics. For both, we report probabilities that state what would happen if we used the inference method repeatedly.
In this section, we build on the ideas in “Distribution of Sample Proportions” to reason as we do in inference, but we do not do formal inference procedures now. Instead, we focus on the logic of inference. We use categorical data and proportions to investigate the logic of inference. But all of the ideas we discuss here apply to quantitative variables and means.
Confidence Intervals
When our goal is to estimate a population proportion, we select a random sample from the population and use the sample proportion as an estimate. Of course, random samples vary, so we want to include a statement about the amount of error that may be present. Because sample proportions vary in a predictable way, we can also make a probability statement about how confident we are in the process we used to estimate the population proportion.
We can find many examples of confidence intervals reported in the media. Here is an example.
Example
Do You Have Problems Sleeping?

The National Sleep Foundation sponsors an annual poll. In 2011, the poll found that “43% of Americans between the ages of 13 and 64 say they rarely or never get a good night’s sleep on weeknights. More than half (60%) say that they experience a sleep problem every night or almost every night (i.e., snoring, waking in the night, waking up too early, or feeling unrefreshed when they get up in the morning” (as reported at www.sleepfoundation.org).
Are these percentages sample statistics or population parameters? These statistics describe the responses of a sample of Americans.
Let’s focus on the 60% who say they experience a sleep problem every night or almost every night. Does this mean that 60% of all Americans have this same experience? Well, no. This is a sample statistic from a poll. But from this sample, we want to infer what percentage of the population does have sleep problems. Since the percentage with sleep problems will differ from one sample to the next, we need to make a statement about how much error we might expect between a sample percentage and the population percentage.
In the “Poll Methodology and Definitions” section of the article, we find more detailed information about the poll. According to the Sleep Foundation website, “The 2011 Sleep in America® annual poll was conducted for the National Sleep Foundation by WB&A Market Research, using a random sample of 1,508 adults between the ages of 13 and 64. The margin of error is 2.5 percentage points at the 95% confidence level.”
There is a lot of important information here:
- The sample is random.
- The sample size is 1,508.
- The margin of error is 2.5%.
- The confidence level is 95%.
From this information, we can construct an interval that we are reasonably confident contains the population proportion.
- Sample statistic ± margin of error
- 60% ± 2.5%
- 57.5% to 62.5%
This interval is an example of a confidence interval. We interpret the interval this way: We are 95% confident that between 57.5% and 62.5% of all Americans experience a sleep problem every night or almost every night.
How confident are we that this interval contains the population proportion? In this case, we are 95% confident. This means that 95% of the time, a random sample of this size will have at most 2.5% error. So 95% of these intervals will contain the true population proportion. Another way to say this is that this method accurately estimates the population proportion 95% of the time.
Note: Notice that the sample is a random sample. We can construct a confidence interval only with a random sample.
Try It
Try It
Summary
A sample proportion from a random sample provides a reasonable estimate of the population proportion. We do not expect the sample proportion to be exactly equal to the population proportion, but we expect the population proportion to be somewhat close to the sample proportion. The purpose of confidence intervals is to use the sample proportion to construct an interval of values that we can be reasonably confident contains the true population proportion.
What Is the Connection to the Sampling Distribution?
Sample proportions are estimates for the population proportion, so each sample proportion has error. For an individual sample, we will not know the exact amount of error, so we report a margin of error based on the standard error. Recall that the standard error is the standard deviation of sampling distribution. We can view the standard error as the typical or average error in the sample proportions. To see how this works, let’s return to a familiar sampling distribution.
Recall our previous investigation of gender in the population of part-time college students. We investigated these questions: What proportion of part-time college students are female? If we predict that the proportion is 0.60, how much error can we expect to be confident of in our prediction?
We predicted the population proportion was 0.60 and ran a simulation to examine the variability in sample proportions for samples of 100 part-time college students. Here is the sampling distribution from the simulation.
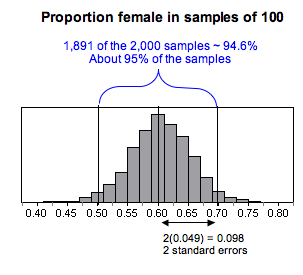
We see that we can be very confident that most samples of this size will have proportions that differ from 0.60 by at most 2 standard errors. For this simulation, the standard error in sample proportions was about 0.049. About 95% of the samples have an error less than 2(0.049) = 0.098
If we use two standard errors as the margin of error, we can rewrite the confidence interval.
- sample statistic ± margin of error
- sample proportion ± 2(standard errors)
- sample proportion ± 2(0.049)
- sample proportion ± 0.098
Different sample proportions give different intervals. For example, if the sample proportion is 0.57, the confidence interval is 0.472 to 0.668. Here are our calculations.
- sample proportion ± margin of error
- 0.57 ± 2(0.049)
- 0.57 ± 0.098
The endpoints of the interval are 0.57 ‑ 0.098 = 0.472 and 0.57 + 0.098 = 0.668. The confidence interval is 0.472 to 0.668.
Since about 95% of the samples have at most 9.8% error, we have a 95% confidence interval. Based on this sample, we say we are 95% confident that the percentage of part-time college students who are female is between 47.2% and 66.8%.
Try It
Try It
- Concepts in Statistics. Provided by: Open Learning Initiative. Located at: http://oli.cmu.edu. License: CC BY: Attribution
